== 証明の進め方 ==（平行四辺形の証明問題2）
○はじめに
（平行四辺形の定義）
　「２組の向かい合う辺がそれぞれ平行である四角形」を平行四辺形という．
（平行四辺形の性質１）
　「２組の向かい合う辺がそれぞれ等しい．※
（平行四辺形の性質2）
　「２組の向かい合う角がそれぞれ等しい．
（平行四辺形の性質3）
　「２つの対角線がそれぞれの中点で交わる．
（平行四辺形の性質4）
　「１組の向かい合う辺が平行で等しい．※

　上のまとめに示したように「平行四辺形」の定義は「２組の向かい合う辺がそれぞれ平行である四角形」すなわち「AD//BC , AB//DC」が成り立つ四角形なので，仮定や結論が「平行四辺形」になっているときは「AD//BC , AB//DC」に置き換えるとよい.

　この頁では平行線の性質について，証明の進め方のあらすじを練習する．

例１
　「平行四辺形の２組の向かい合う辺はそれぞれ等しい」という性質を証明したいときは，
「AD//BC , AB//DC」から
△ABCと△CDAが
「１辺とその両端の角がそれぞれ等しい」ことから
合同であることを示し，
これによって「AD=BC , AB=DC」を示せばよい．※※


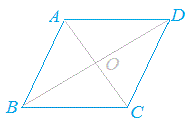
※　辺については長さが等しいことを単に「等しい」という．

※※　左の例１で△ABC≡△CDAを示すときに，
（ア）　「３辺がそれぞれ等しい」ことは使えない．（AD=BC , AB=DCは証明すべき式だから使えない．）
（イ）　「２辺とその間の角がそれぞれ等しい」ことは使えない．（AD=BC , AB=DCは証明すべき式だから使えない．）
（ウ）　辺の長さとして使えるのはACが共通ということだけだから「１辺とその両端の角がそれぞれ等しい」ことによって示すことになる．
■問題■
　四角形ABCDについて左欄の性質を証明したいとき，どのように証明を進めるとよいか．右の欄から選びなさい．
（なお，証明方法はいろいろありますが右欄の中では１つです．）



 【注意：速くやると間違うので，１分以上かけて読むこと】
○===メニューに戻る