|
■サイコロの基本問題■
【例題1】
(解答)大小2つのさいころを同時に投げる。 ① 略 ② 出る目の和が10の約数になる確率を求めなさい。ただし,さいころの1から6までのどの目が出ることも同様に確からしいものとする。 (熊本県2017年入試問題)
起こり得るすべての場合の数は36通り そのうちで10の約数になる場合は8通り 確率は
さいころを2つ投げる場合,6×6形の上のような表を書いて,結果を整理すると分かりやすいので,この表に慣れておくとよい
右上に続く↑
※以下の問題では,マウスでクリックして解答すれば解説が出ますが,解答しなければ解説は出ません.
|
※以下に引用する高校入試問題で,元の問題は記述式の問題ですが,web画面上で入力問題にすると操作性が悪いので,選択問題に書き換えています.
【問題1】 (画面上で解答するには,選択肢の中から正しいものを1つクリック)
(1)
A,B二つのさいころを同時に投げ,Aのさいころの出る目の数をa,Bのさいころの出る目の数をbとするとき, (大阪府B 2017年入試問題)
したがって,確率は |
 (考え方)
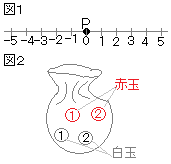
(考え方)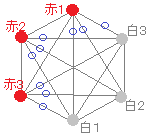 赤球と白球が1個ずつとなる組合せは
赤球と白球が1個ずつとなる組合せは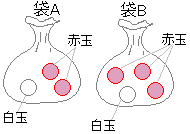
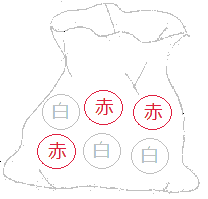
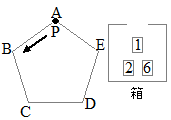
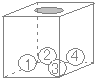 右の図のように,1, 2, 3, 4の数字が書かれた4個の玉が箱の中に入っている。この箱の中の玉をよくかきまぜてから1個取り出し,玉に書かれている数字を調べ,それを箱に戻してからまた,1個取り出して,その玉に書かれている数字を調べる。はじめに取り出した玉に書かれている数字を十の位の数,次に取り出した玉に書かれている数字を一の位の数として,2けたの整数をつくるとき,24以上の整数になる確率を求めなさい。
右の図のように,1, 2, 3, 4の数字が書かれた4個の玉が箱の中に入っている。この箱の中の玉をよくかきまぜてから1個取り出し,玉に書かれている数字を調べ,それを箱に戻してからまた,1個取り出して,その玉に書かれている数字を調べる。はじめに取り出した玉に書かれている数字を十の位の数,次に取り出した玉に書かれている数字を一の位の数として,2けたの整数をつくるとき,24以上の整数になる確率を求めなさい。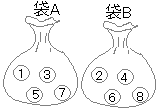 右の図のように,2つの袋A,Bがあり,袋Aの中には,1, 3, 5, 7 の数字が1つずつ書かれた4個の玉が,袋Bの中には, 2, 4, 6, 8 の数字が1つずつ書かれた4個の玉が入っている。この2つの袋の中からそれぞれ玉を1つずつ取り出すとき,袋Aの中から取り出した玉に書かれた数を
右の図のように,2つの袋A,Bがあり,袋Aの中には,1, 3, 5, 7 の数字が1つずつ書かれた4個の玉が,袋Bの中には, 2, 4, 6, 8 の数字が1つずつ書かれた4個の玉が入っている。この2つの袋の中からそれぞれ玉を1つずつ取り出すとき,袋Aの中から取り出した玉に書かれた数を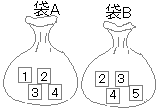 右の図のように,1, 2, 3, 4 の数字が1つずつ書かれた4枚のカードが入っている袋Aと,2, 3, 4, 5 の数字が1つずつ書かれた4枚のカードが入っている袋Bがある。
右の図のように,1, 2, 3, 4 の数字が1つずつ書かれた4枚のカードが入っている袋Aと,2, 3, 4, 5 の数字が1つずつ書かれた4枚のカードが入っている袋Bがある。
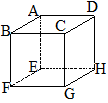 図のような立方体があり,点
図のような立方体があり,点
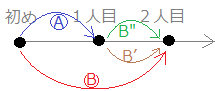 ※ここで述べている話は,右図でまだ誰もくじを引いていない「初め」と書いた時点から未来に向かって投げかけられた確率AとBは等しいということ
※ここで述べている話は,右図でまだ誰もくじを引いていない「初め」と書いた時点から未来に向かって投げかけられた確率AとBは等しいということ