|
※この頁は直線の傾きの発展学習です.もし難しいと思ったら,もっと前の頁を先に勉強してください. (一つ選んでクリックしなさい)  原点を通る直線y=axが線分AB(両端を含む)と交わるとき
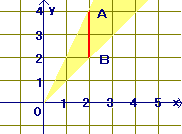
原点を通る直線y=axが線分AB(両端を含む)と交わるとき(1) 傾きが最も小さくなるのは図のOBとなる場合で,そのときの傾きは (2) 傾きが最も大きくなるのは図のOAとなる場合で,そのときの傾きは したがって,1≦a≦2 ※何か便利な公式があるのかと考えてはいけない.教科書に出ていないような公式は勝手に使えない.この問題では,図を見て「傾きが小さいとき」「傾きが大きいとき」を目で見て考えて,階段の絵を描いて,縦÷横で傾きを計算する. |
 1.
1.
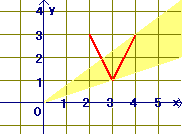 2.
2.
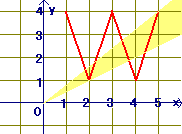 3.
3.
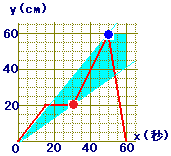
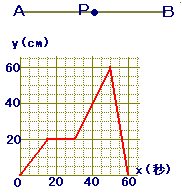 4. 長さ60cmの線分ABがあり,点Pは,線分AB上を動くものとする.右のグラフは,点Pが点Aを出発してから経過した時間をx秒,点Aからの距離をycmとしたときの,x,yの関係を示したものである.次の各問いに答えなさい.
4. 長さ60cmの線分ABがあり,点Pは,線分AB上を動くものとする.右のグラフは,点Pが点Aを出発してから経過した時間をx秒,点Aからの距離をycmとしたときの,x,yの関係を示したものである.次の各問いに答えなさい.