|
【例題1】
関数
(解答)(茨城県2015年入試問題)
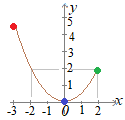
x=−3のとき, x=2のとき,y=2…(B) x=0のとき,y=0…(C) グラフは右図のようになるから |
 【要点】
【要点】1. 2次関数y=ax2で,a>0の とき(この問題では 2. xの変域が与えられたとき,yの変域は,右図で赤●,青●,緑●で示した3つの点,すなわち「左端」「右端」「頂点」のy座標のうちで最小値から最大値までです. (1) まず左端,右端以外に頂点の値も候補に入れて,そのうち2つの値を答えることになります.(候補者3人のうちで当選するのは2人だけです) 中間になる値(右図では緑●)はyの変域に影響しません. (2) xの変域が頂点を含んでいるときは,頂点のy座標が最小値になります. (3) 問題に書かれたxの値の順に関係なく,変域としてyの値の順に並べることが重要です. |
|
※以下に引用する高校入試問題で,元の問題は記述式の問題ですが,web画面上で入力問題にすると操作性が悪いので,選択問題に書き換えています.
【問題1】 (画面上で解答するには,選択肢の中から正しいものを1つクリック)
(1)
関数 (奈良県2015年入試問題)
|
(2)
関数y=3x2について,xの変域が−4≦x≦2のときのyの変域はa≦y≦bである。このとき,a, bの値をそれぞれ求めよ。 (高知県2015年入試問題)
 x=−4のとき,y=48…(A)
x=−4のとき,y=48…(A)x=2のとき,y=12…(B) x=0のとき,y=0…(C) (A)(B)(C)よりグラフは右図のようになるから 0≦y≦48 a=0, b=48 …(答) |
|
(3)
関数y=x2について,xの変域が−5≦x≦4のときのyの変域を,次のア〜エのうちから選び,記号で答えよ。 ア −25≦y≦16
イ 0≦y≦16
ウ 0≦y≦25
エ 16≦y≦25
(東京都2015年入試問題)
|
(4)
関数 (福岡県2015年入試問題)
|
|
【例題2】
関数y=−x2について,xの変域が1≦x≦3のときのyの変域を求めなさい。
(解答)(栃木県2015年入試問題)
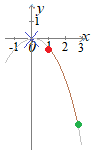
x=1のとき,y=−1…(A) x=3のとき,y=−9…(B) グラフは図のようになるから −9≦y≦−1…(答) |
 【要点】
【要点】1. 2次関数y=ax2で,a<0の とき(この問題ではa=−1),グラフは右図のように山型(上に凸)になります. 2. xの変域が与えられたとき,yの変域は,右図で赤●,緑●で示した2つの点,すなわち「左端」「右端」のy座標のうちで最小値から最大値までです. (1) 頂点の値(右図では青×)はyの変域に影響しません. (2) この問題のように減少関数(xが増えたらyが減る)になるような変域もありますので,問題に書かれたxの値の順に関係なく,変域としてyの値の順に並べることが重要です. |
|
※以下に引用する高校入試問題で,元の問題は記述式の問題ですが,web画面上で入力問題にすると操作性が悪いので,選択問題に書き換えています.
【問題2】 (画面上で解答するには,選択肢の中から正しいものを1つクリック)
(1)
関数y=−x2について,xの変域が−2≦x≦1のときのyの変域を求めなさい。 (岩手県2000年入試問題)
|
(2)
関数y=−x2について,xの変域が−3≦x≦aのとき,yの変域が−16≦y≦bである。このとき,a, bの値を求めなさい。 (神奈川県1999年入試問題)
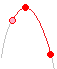 x=−3のとき,y=−9≠−16…(A)
x=−3のとき,y=−9≠−16…(A)だから, x=aのとき,y=−16…(B) ただし,−3≦x≦aだから,a≠−4 したがって,a=4 x=0のとき,y=0…(C) だから,b=0 以上から a=4, b=0 …(答) |
|
(3)
xの変域が−1≦x≦3のとき,関数y=−4x2のyの変域を求めよ。 (広島県1999年入試問題)
|
(4)
xの変域が−3≦x≦−1のとき,関数y=−2x2のyの変域を求めよ。 |