→ �g�є�
|
|
���@�̗p����邩�ǂ����͓��e�������ł��D��҂ɓs���̂悢�ӌ����̗p�����Ƃ͌���܂��C�U���I�ȕ��͂₷�łɉ��x�����Ă�����e�Ɠ���̂��̂Ȃǂ͎��グ�Ă��܂���D
���@�����v�]�ɑ���́C���Ȃ������w���Ȃ̂����Z���Ȃ̂��Љ�l�Ȃ̂��ɂ���ĕς邱�Ƃ������̂ŁC���M�҂̔N��܂��͗�����Y�ꂸ�ɋL�����Ă��������D
�@�܂��u����łŁv�Ƃ��u����̕łŁv�Ȃǎw�����e�������܂��Ȏ���ɂ͑Ή��ł��܂���B�K���ł̑薼��URL�ihttp://����j����肵�Ď��₵�Ă��������B
|
�����j���[�ɖ߂�
�i�����t�̐V�������̂���\���j
���m�ʂ̕ł���̎���ɑ���n[�������̑召��r1�ɂ��ā^24.04.21
������chrome browser�ł��̃T�C�g�𗘗p���ĕ��ɗ��ł�����̂Ȃ�ł��A�ŋ߂��낢�덀�ڂ����������ł������X���������锤�̏��X����ɕ�����ł���_�Ƒ����̃C���[�W�ŏo�Ă��܂��Ăɍ����Ă���܂��B
����ŁA����͎����̖��Ȃ̂�����Ƃ����̃T�C�g�̖��Ȃ̂����͂킩��܂���
�����琥��Ƃ��T���Ē����Ă������邩�A���̍����������Ă������������Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��DGoogle�̐����\���T�[�r�X���C�~�܂��Ă���悤�ŕM�҂������Ă��܂��D���݁C�@GoogleAPIs���ˑR�T�[�r�X���~����Ɖe���͑傫���ł��D�Ȃ��C�AMathML�̕��́C�̂�MathPlayer�̃v���O�C�����C���X�g�[������Ȃ����]�Ȑ܂��������悤�ł����C2009�N���납��jsMath�ɋz������CMathaJax�Ƃ��Ă���Ă���悤�ŁC�����ނł́C�@�����߂Ȃ�A�ŕ\������悤�ɏ���������ƒ��ł��D���Z���w�T�CA�̕ӂ�܂Ői��ł��܂����C���w�V�Ƃ����w���w�܂ŏ���������ɂ́C���N��t������ł��傤--1�y�[�W�ӂ�̐��������ς�200�قǂ����āC�S���Ő���[�W����C�o�b�`�����������Ȃ悤�ł��D�i�@���A���_���ȏꍇ�C�B���͂ŕ����C������\��������@������܂����C�u���E�U�̃V�F�A�̕ϑJ�Fnetscape→IE→Chrome, Edge����т��̑��l�ȃo�[�W�����ɉ����ďc�����̕\���ʒu���ς�邽�߁C�������ςł��D���ǁC�@�D��C�G���[���A�̕����ŁC�����������ď���������ƒ��Ƃ������Ƃł��j
���m�ʂ̕ł���̎���ɑ���n[�f���������ɂ��ā^24.03.21
�f���������̌��ɂ��Ď��₳���Ă����������҂ł��B�����^������̐����悭�킩��܂����B�Q�l�ŏ����ꂽ�W���̌����A���߂Ċ��Ⴂ�ɋC�Â�����܂����B���肪�Ƃ��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�f���������ɂ��ā^24.03.20
�����b�ɂȂ�܂��B�f���������ɂ��Ď��̗����Ő������̂��m�F�����Ă��������B2�ȏ�̎��R���ɂ����āA�f���ł͂Ȃ����������f���������A�܂�f���̐ςŕ\����B�]����3�Ƃ�5�Ƃ�7�Ƃ������f���͑f���������ł��Ȃ��B�܂��Q�ȏ�̎��R���őf���������ł���ŏ��̐���4�ł���B
�����m��ҁn�F�A�����肪�Ƃ��D�����^������n�߂܂��傤
1. (1) 100�~��20�~��5�~������Ƃ��C�u���v���z�v��125�~�ł��D (2) 20�~��5�~������Ƃ��C�u���v���z�v��25�~�ł��D (3) 5�~������Ƃ��C�u���v���z�v��5�~�ł��D�������̂��Ȃ�����u�Ȃ��v�Ƃ͂��܂���D
2.�@1����n�܂ł̐��̐����̐ς��K��Ƃ����Cn!�ŕ\���i���Z1�N�ŏK���j�D���̂Ƃ��C(1) 3!=3�~2�~1=6 (2) 2!=2�~1=2 (3) 1!=1�Ƃ��܂��D1�ł͊|�����Ȃ�����u�Ȃ��v�Ƃ͂��܂���D
�@���āC�u�����_�̊�{�藝�v�ł́u2�ȏ�̐��̐����͑f���̐ς̌`�ŕ\�����Ƃ��ł��C���̕\�����͏����������C����1�ʂ�Ɍ��܂�v�Ƃ���Ă��܂��D���̏ꍇ�C6=2�~3, 4=22�ȂǍ������́C2�ȏ�̑f���̐ςŕ\����܂����C�u2, 3, 5, ..�Ȃǂ̑f���́C�����f���������ł��Ă��邩��C����ȏ�͕����ł��Ȃ��v�Ƃ���̂��u���ʂ̍l�����C���ʂ̌����v�ł��傤�D��L�̐����_�̊�{�藝�̌�������l����ƁC�u�f���͑f���������ł��Ȃ��v�Ƃ͌���Ȃ��̂����ʂł��傤�D
�i�Q�l�j
�@���ł́C�������̍��ڂŁC�Ⴆ��3x��3�̂悤�ɕ����Ɋ|���Ă�����̂��u�W���v�Ƃ�����`������D���̒�`�ɂ����āu�����Ɋ|���Ă���v�Ƃ������t���撣��߂��Ă͂����Ȃ��D���w1�N��������Ȃ��悤�ɁC������₷���C�������茾�����܂łŁC�u�����Ɋ|���ĂȂ����̂͌W���ł͂Ȃ��v��3x2+4x+5�ŁC3, 4�͌W�������C�萔����5�͌W���łȂ��ȂǂƁC�c�{�łȂ��Ƃ����͔C���ɉ����Ă��C��������͉̂�������܂���D�����łȂ��������W���ł�����C���Z���w�ł́C3x2+4x1+5x0��3, 4, 5�͌W���ł��D
�@���̂悤�ɁC�ς�a���܂ޗp��̎g�����Ƃ��āC1�C0�̏ꍇ�ɂ��g���ł���Ƃ��́C�g���ł���g�����ŗ������܂��D�l�b�g��ł͊w�K�m�ł̋������H�Ƃ��āC�u�萔���͌W���łȂ��v�ƔM���I�Ɋ撣���Ă�����L�������������܂����C���̍s�����ł͍��Z�ɂȂ����Ƃ��ɁC���܂ŏK�������Ƃ͉R�ł��̂ŖY��Ă��������ƌ����K�v������C�ЂƎ�Ԃ����邱�ƂɂȂ�܂��D
���m�ʂ̕ł���̎���ɑ���n[�����i�S����,����,�����j�ɂ��ā^24.03.12
90g��300g�́�%
48�{�́��{��120%
�����m��ҁn�F���₪����Ȃ�C���t�Ō���Ȃ��ƁC�ʂ��܂���D����Ƃ�,���ނɊԈႢ������Ƃ������Ƃ��w�E���Ă���̂ł����H
�@�Ƃ肠�����C���̋��ނɏ����ĂȂ����ɂ��āC�Ⴆ�ΐ��k�̏h��̓�����������悤�Ȃ��Ƃ́C�_���Ȃ̂ŁC�Ⴄ���̉������������܂��D��������āC�����ōl���Ă��������D
�@�u80g��400g�́�%�v �� 80=400�~x �� x=80��400=0.2 �� 20%
�@�u30�{�́��{��150%�v �� 30=y�~1.5 �� y=30��1.5=20 �� 20�{
���m�{�錧�^��g����^24.03.12
���ԐM���肪�Ƃ��������܂��B���������Ă�������A���肪�Ƃ��������܂��B
���̃T�C�g��q�����āA�쐬�җl�̐��w�i��p��j�A�����Ďq�ǂ��������w��`���邱�Ƃւ̈��Ə�M���ƂĂ������������܂����B���Ў��ƂŊ��p���A�q�ǂ������̐��w�͂����߂��������Ǝv���܂��B����Ƃ���낵�����肢�������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D���J�^��Web���ނ́u���Ă�����Ă������藧�v�̂ŁC�ǂ�ǂĂ��������D
���m�{�錧�^��g����^24.03.10
���������Ă��܂��B�ƂĂ��悢�T�C�g���Ǝv���܂����B
���Ƃ̒��ł��̃T�C�g�ɂ������������Ǝv�����̂ł����A���쌠���̖��͂���܂��H����낵�����肢���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D���̍l���́C20�N�ȏ�O�ɂǂ����̓s���{������Z���^�[�ŁC���S���҂�Ǘ��E�����ɒ��쌠�@�̊T�����u�`���Ă��������̒m���Ȃ̂ŁC�ŐV�̉����܂��Ă��܂���̂ŁC���̓_��낵���D
�@�܂��C���쌠�@��35������{�ł�
�u�w�Z���̑��̋���@�ցi�c����ړI�Ƃ��Đݒu����Ă�����̂������B�j�ɂ����ċ����S�C����ҋy�ю��Ƃ���҂́A���̎��Ƃ̉ߒ��ɂ����闘�p�ɋ����邱�Ƃ�ړI�Ƃ���ꍇ�ɂ́A���̕K�v�ƔF�߂�����x�ɂ����āA���\���ꂽ���앨�����A�Ⴕ���͌��O���M�i�������O���M�̏ꍇ�ɂ��ẮA���M�\�����܂ށB�ȉ����̏��ɂ����ē����B�j���s���A���͌��\���ꂽ���앨�ł��Č��O���M�������̂���M���u��p���Č��ɓ`�B���邱�Ƃ��ł���B�������A���Y���앨�̎�ދy�їp�r���тɓ��Y�����̕����y�ѓ��Y�����A���O���M���͓`�B�̑ԗl�ɏƂ炵���쌠�҂̗��v��s���ɊQ���邱�ƂƂȂ�ꍇ�́A���̌���łȂ��B�v
�v��C�u���Ƃ�S������҂��C���Ƃ̒��Ŏg�����߂ɁC���\���ꂽ���앨�����Ďg���͍̂\��Ȃ��v�ƂȂ�܂����C�u���Ƃ�S�����Ȃ��ҁF�Ⴆ�Ύs��������ψ���̎����ǂ��܂Ƃ߂ăR�s�[����̂̓_���v�u�w�Z������w�Z�s���Ɏg���ꍇ�͑�35���̓K�p�O������_���v�ȂǂƂȂ�܂��D�܂��C��ʂɉ摜�C�y���C�\�t�g�E�F�A�̂悤�Ȃ��̂̕����͐����������Ȃ�C�s�̖̂��W�����邱�Ƃ��F�߂��܂���D
�@���̋��ނɊւ��ẮC�R���s���[�^�[������e���̐��k�����ړǂނ̂́C�S����肠��܂��C������Ƃ��Ďg�����Ƃ����Ȃ��ł��D���쌠�@�̌��O���猾���C�m��\���Z�ɂ����āC���앨������ꍇ�́C��35���̑z�肷��͈͂ł͂Ȃ��Ƃ���Ă��܂��D
�ō��ł� ���肪�Ƃ��������܂�
�����m��ҁn�F�A�����肪�Ƃ��D�ڂƂ����L�����ǂ݂ɂ��������̂ŁC���łɒ����܂����D
���m�ʂ̕ł���̎���ɑ���n[���ʐ}�`�̗p���ɂ��ā^24.02.12
�e�X�g�̕��Ƀs�b�^���������B�}�[�N�V�[�g�Ȃ̂łȂ����肪�����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�m���̗Z������ɂ��ā^24.02.06
���S�́i�Q�j�̖�蕶���Ԉ���Ă���Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�u�O�p�`���ƌ����Ă���̂�����C�O�p�`�ɂȂ�͓̂��R�v�Ƃ������ƂŁC�u�\���̎d�������������v�̂ŁC�������܂����D
���m�ʂ̕ł���̎���ɑ���n[���̂̑̐ρi�������j�ɂ��ā^24.02.06
�ŏ��̖��� ���� �ł͂Ȃ��Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�����ƂƁC�_���~�X�ł����̂Œ������܂���
���m�ʂ̕ł���̎���ɑ���n[�������ɒ������K�ɂ��ā^24.02.04
���̎Q�l�ɂȂ�܂����I���肪�Ƃ��������܂����I�I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�_�Ώ̂Ȑ}�`�ɂ��ā^24.02.04
�Q�l�ɂȂ�܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����}�`�ƕӂ̔��ɂ��ā^24.02.02
�����`��ς��Ă��铯�����e�̖����R��������ƂłP��ځA�Q��ڂŊԈ���Ă����i�R�j�̖�肪���R�́i�R�j�ʼn�����悤�ɂȂ�܂����B
�m����������₷�������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D��҂���Ԋ�т����Ȋ��z�ł��D
���m�ʂ̕ł���̎���ɑ���n[�m��(���Z�������)�ɂ��ā^24.01.21
�܂Ƌʂ̖��̂Ŗ�肪�����ĂȂ������ł��B�����������ƂȂ��ł��Ė�肪�Ȃ��̂ʼn̂��悤���Ȃ��̂őI���ł��܂���ł����B
�����m��ҁn�F�A�����肪�Ƃ��D���̌����͂킩��܂��C������ł͐���ɕ\������܂��D�Ȃ��C���̖��ƒ��ڂ̊W�����邩�Ȃ����͕�����܂��Cwindwos�ł�safari�́C���Ȃ�O����Apple�ɂ��T�|�[�g���Ȃ���Ă��Ȃ��Ƃ������ƂŁC�M�҂��g��Ȃ��悤�ɂ��Ă��܂��D
���m�ʂ̕ł���̎���ɑ���n[�ω��̊���(�������)�ɂ��ā^24.01.16
�����Ɩ��̂��Ă��������I�킩��₷�������ł��I
�����m��ҁn�F�A�����肪�Ƃ��D���������Ă���C���̃y�[�W�i�ψ�Ȃǁj�ɐi�ނ悤�ɂ���Ƃ悢�ł��傤�D
���m�ʂ̕ł���̎���ɑ���n[�m��(���Z�������) �ɂ��ā^23.12.29
�m���͋��ȕ���ł������A�����ł��܂����B
�\���g���Ƃ����l�������m�邱�Ƃ��ł��Ă悩�����ł��B
���͏m�ɍs���Ă��炸�w�Z�ł��A���̂悤�ȉ������͋����܂���B
�ƂĂ��킩��₷�������ł��I���肪�Ƃ��������܂���😊
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�ő���ƍŏ����{���ɂ��ā^23.12.16
�ƂĂ�������₷�������ł��B
���肪�Ƃ��������܂����I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�s�����̉������ɂ��ā^23.12.16
�ƂĂ��������₷���A���������g���čl������̂łƂĂ��ǂ��Ǝv���܂��B
����̕�������F�Ȃ̂ŁA�l�X�ȐF���g���ƕ�����₷���Ȃ�Ǝv���܂����B
�����m��ҁn�F�A�����肪�Ƃ��D�F��3�F�܂ŁC�����Ă�4�F�܂łƂ����Ă���C����ɒB���Ă��܂��D
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝(�������) �ɂ��ā^23.11.20
������A�l�ɂ���Ă͕�����ɂ������̂�����̂ŁA���P���Ăق����ł�
�����m��ҁn�F�ǂ������l�ɁC�ǂ�������ɂ����̂��������Ȃ���C�Ή��̂��悤������܂���D���Ƃ��C�u�܂���{�̕������Ă��Ȃ��l���C������肩��n�߂��ꍇ�ɁC�ꂩ�番����Ȃ��̂őS�������Ăق����Ƃ����ꍇ�v�́C�����ƑO�ɏ����Ă����{�̃y�[�W���ɓǂ�ł��������D�u�ԗΐF�o������Ȃ̂ŁC�ԐF�ׂ̗ɗΐF���g��Ȃ��łق����Ƃ����悤�ȏꍇ�v�́C���������Ă��������D�u���͂�����Ō����ɂ����Ƃ����ꍇ�v�͉�ʂ��g�債�ĉ������D�u���w���Ȃ̂ŗ����ł��Ȃ��Ƃ����ꍇ�v�́C�Ή�����\��͂���܂���D
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝(�������)�ɂ��ā^23.11.15
���ݒ��w���ł����A�ƂĂ�������₷���Ă����Ǝv���܂��B👍
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����}�`�Ɗp ==�i�������j�ɂ��ā^23.11.12
����e�X�g�O�łƂĂ����ɗ����܂����B���肪�Ƃ��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D�����e�X�g�C������Ă�������
���m�ʂ̕ł���̎���ɑ���n[�Q���������̉������i�܂Ƃ߁j�ɂ��ā^23.10.29
�����ɍ̓_���Ă����̂ŁA�ƂĂ�������܂���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝(�������)�ɂ��ā^23.10.17
���̂��������߂ɂȂ����B�ƂĂ��킩��Ղ��čō��ł��I�I
����Ŏ��������_�J�i�I�H
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������ɒ������K�i���w�����j�ɂ��ā^23.10.16
������ǂ����Ƃ킩�����̂ŗǂ������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�P�����Ƒ������ɂ��ā^23.10.08
�����́B���w���D���ł�藝����[�߂����v���A���̃T�C�g�ɂ��ǂ蒅�������R�ł��B
�i������j
���̃y�[�W��q�����Ď���ł��B
��2.2�̉�2�����ɂȂ闝�R�����܂��������ł��Ȃ��̂ŁA����������Ɗ������ł��I
�i4�������Ǝv���܂����j
�����m��ҁn�F�A�����肪�Ƃ��D�u2��ވȏ�̕������܂ޒP�����ł́C(2) ����̕����ɒ��ڂ��Ď������l����Ƃ��́C���ڂ��������̌��������Ƃ����C�c��̕����Ɛ������W���Ƃ��Ĉ����D�v�y��1.3.1�z�y��1.3.2�z�Ȃǂ����ƑO�̖����ɂ���Ă��������D�܂��C���̖��̉����Ă��������D
���m�ʂ̕ł���̎���ɑ���n[�Q���������̓�������ɂ��ā^23.10.05
��b���牞�p�܂Ŗ�肪�����ėǂ��Ǝv���܂��B�������A�������Ȃ̂�(x+a)(x +t)��0 �Ȃǂ̂悤��(a�At �͐����Ƃ��܂�)���͂قƂ�ǂł���ł��낤�l�������قƂ�ǂ��Ǝv���̂ł��������P�������e�ɂ��Ă������������ł��B�����ɓ������o�Ă��܂��ė��K�ɂ��Ȃ�Ȃ��ȂƎv����肪���₠��܂����B�ł����A�S�̓I�ɂƂĂ��ǂ������Ǝv���܂��B�V���v���ʼn�����킩��₷�������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D���Z���������W�߂����̂́C���Z�����ɏo����肵���o���܂���D�Ȃ��C��������悢�ꍇ�́C���Z�̖������Ă��������D
���m�ʂ̕ł���̎���ɑ���n[�������̕\�����ɂ��ā^23.09.19
�킩��₷�������Ă���̂ł����Ƃ������܂��B
������܂����B�@m(_ _)m
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������̍����ɂ��ā^23.09.18
����1���蒼�����@�\���~�����ł�m(_ _)m
�����m��ҁn�F�A�����肪�Ƃ��D�����[�h���Ă��炤�ƁC����ł������Ԃ�܂�������@�\�H�������̋ƊE�p��
���m�ʂ̕ł���̎���ɑ���n[�A���������̍���������͑��ɂ��ā^23.09.18
A����͉Ƃ��ߑO7��50���ɏo�����āA2000m���ꂽ���w�Z�Ɍ��������B�n�ߕ���70m�o�����Ă������A�x���������ɂȂ����̂œr�����番��200m�ő���A�ߑO8��13���Ɋw�Z�ɂ���
�����m��ҁn�F�@����Ȃ̂����Ȃ̂������Ȃ���Ε�����܂���D�A���₾�Ƃ��Ă��C�������߂����̂������Ȃ���Ε�����܂���D�B�A���������̍������Ă���̂��C���������Ă���̂�
���m�ʂ̕ł���̎���ɑ���n[�Q�_�Ԃ̋����ɂ��ā^23.09.16
������������
�����m��ҁn�F�A�����肪�Ƃ��D���̃y�[�W�̐擪�Ɂu�g�єł͕ʕŁv�Ə����Ă���܂��̂ŁC�g�їp�̃y�[�W�����Ă��������D360x720��Android�Ńp�\�R���p��ʂ�������C�����͏����������܂��D
���m�ʂ̕ł���̎���ɑ���n[�s�����̉������ɂ��ā^23.09.11
�r������������킩��₷���Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D���ނ̎g������������Ȃ��悤�ł��̂ŁC�������܂�.���̏�ɏ����Ă���܂��悤�Ɂi�I�����̒����琳�������̂��P�N���b�N�j�ł��D����C�̓_���ʂƓr���o�߂��\������܂����C���Ă��邾���ʼn��Ȃ���i�N���b�N=�^�b�v���Ȃ���j�C�̓_���ʂ��r���o�߂��\������܂���D�Ȃ��C�����Ȃ�iPhone�ł��̂ŁC�p�\�R���p���ނł͂Ȃ��C���̃y�[�W�̐擪�ɏ����Ă���悤�ɁC�c���\���̌g�їp���ނ�����������₷���ł��傤�D
���m�ʂ̕ł���̎���ɑ���n[���l���E�X�̒藝,�`�F�o�̒藝�ɂ��ā^23.09.10
�ƂĂ�������₷�������B
�����A�����������W���������̂��Ă���Ƃ�艞�p�������悤�ɂȂ邩�ȂƎv�����B
�����m��ҁn�F�A�����肪�Ƃ��D���̃y�[�W�̐擪�ɏ����Ă��܂��悤�ɁC���w���p�̋��ނƂ��āC���l���E�X�̒藝,�`�F�o�̒藝�C���ꎩ�̂��o�肷�邱�Ƃ͂��蓾�܂���D���e�I�Ȕ��W�≞�p�����蓾�܂���D���w�������̋��ނƂ��ẮC���}�`�̉��p���Ƃ��ĉ�����͈͂Ɍ����܂�.�O�����̒藝�ŁC�ŋ߂̍��Z�������Ɍ�����X���̂悤�ɁC��Ԑ}�`�Ƒg�ݍ��킹����C�}�`��v�Z�G�ɂ��āC�������ԓ��ɏ����ł��Ȃ��悤�ɂ�����x�����W�E���p�Ƃ������Ƃ̈Ӗ��ł��D
�@Web���ނȂ̂ŁC��l�̕����ǂ܂��͎̂��R�ł����C���̃y�[�W�͒��w�������̋��ނł��̂ł�낵���D
���m�ʂ̕ł���̎���ɑ���n[�������ɒ������K�i���w�����j�ɂ��ā^23.09.08
�������番���ɂł��錴�����S���킩�炸���̃T�C�g��q�������Ă����������̂ł��������킩��₷�������ł��I
���肪�Ƃ��������܂���😊
�����m��ҁn�F�A�����肪�Ƃ��D�ׂ��Ȓ��ӂł����C������2,3�l�̂悤�ɏ��Ȃ����C�����͐����╪���ƈ���ď����_�ȉ����g���ď�����鐔�D
���m�ʂ̕ł���̎���ɑ���n[�Q���������̉������i�܂Ƃ߁j�ɂ��ā^23.09.08
�|���}�C�i�X�Ƃ��Ĕ��肳��܂���
�����m��ҁn�F�A�����肪�Ƃ��D���̖��ł́u���p�����v�i1�o�C�g�����C�A�X�L�[�����j�œ����Ă��������̂���{�Ƃ��Ă��܂����C�Ή�����S�p�����̐����ʼn��ꂽ�ꍇ�ł��C���p�����ɒ����č̓_���Ă��܂��D���āC��������͂悭���Ă��Ă��C�قȂ镶���ɂȂ��Ă��邱�Ƃ�����܂��D�Ⴆ�C�u��v�u�[�v�u-�v�u�\�v�u�Q�v�u�|�v�́C���Ɂu�������̈�v�u�J�^�J�i�Ń��[�}�̂悤�Ȓ�����\���ꍇ�v�u���p�����̃}�C�i�X�v�u�n�C�t���v�u�A���_�[�o�[�v�u�S�p�����̃}�C�i�X�v�Ȃǂ悭��������������̂Œ��ӂ��K�v�ł��D�m���Ƀ}�C�i�X�ɑΉ�����̂́u�e���L�[�v�i������+-*/���W�߂����́j����I�ꍇ�ł��D
���m�ʂ̕ł���̎���ɑ���n[�������ɒ������K�ɂ��ā^23.09.05
�킩��₷�����A�Q�l�ɂȂ�܂��B���肪�Ƃ��������܂�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[����ɍ����̂Ȃ��`�ɂ��ā^23.09.01
��[�ƂV�Q�Ԃ�̂T
�����m��ҁn�F���₪����Ȃ�C����ł��Ə����Ȃ��ƥ������ɁC

�Ȃ̂�

�Ȃ̂��������Ȃ��ƥ�����̎����͉ċx�݂̏h���o���T���Ă��āC�������蓚����������Ɣᔻ���邱�Ƃ�����D��Ȃ���Ȃ�
������傫�����Ăق����ł�
�����m��ҁn�F�A�����肪�Ƃ��DiPad�ŕ�����傫������̂́C�ȒP�Ȃ͂��ł����H��ʂ��c�^�i�|�[�g���[�g�j�ɌŒ肵�Ă���ꍇ�́C�u�g�їp�͕ʕŁv�Ƃ����ē��ɉ����Č��Ă��������B
���m�ʂ̕ł���̎���ɑ���n[�A���������̕��͑�2�ɂ��ā^23.08.28
�킩��₷������
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�O�p�ɂ��ā^23.08.11
���p�`�̒��w���w�ł̎戵�����ɂ��āA�F�X�ȋ��ȏ������m�F���������������Ł@����Ȃɑ�������������Ǝv���Ă��݂܂���ł����B�������ł�����₵�Ă����̂���������ł��A��ς��肪�Ƃ��������܂����B
�����łŐ\����܂��A���p�`�̊O�p�̘a�ɂ��Ă������Ă��������B���p�`�̈�̒��_�̓��p�ɂ��āA��������ޕӂ̂ǂ����L�����ň�̒��_�ɓ�̓����傫���̊O�p���o���܂��B�O�p�̘a�����߂�Ƃ��A�a��360�ɂȂ邱�Ƃ������Ƃ������ꍇ�A�Ȃ��Б���������l���邱�Ƃɂ���̂����R���悭�킩��܂���B���p�ƊO�p�͈�̃y�A�Ȃ̂ŁA��̒��_�ɂ͈�̊O�p�����Ȃ��ƍl����Ƃ������ƂȂ̂ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D�P�̓��p�ɑ��āC�O�p�͂Q������D�u���p�`�̊e���_�ɂ�����O�p���P���Ƃ����a���C���̑��p�`�̊O�p�̘a�Ƃ����܂��v�iK�ЁF���ɂЂ����ɂ��Ă���킯�ł͂Ȃ��j�D
�@�u2������O�p�̂����P�����������̂��O�p�̘a�Ƃ����v�Ƃ����̂���`�Ȃ̂ŁC����ɏ]���݂̂ł�����Q��������2�{�ɂȂ邾���ł����C��`�����߂Ȃ��Ǝ��̘b�ɐi�߂Ȃ��Ȃ�D
���m�ʂ̕ł���̎���ɑ���n[�O�p�ɂ��ā^23.08.10
���w���w�ł͓ʑ��p�`�A�����p�`�̋�ʂɂ��Ă��܂�����������悤�Ɏv���܂��B�O�p�̒藝���g�������ł͉����p�`�ł��鐯�`��u�[�������`���o�Ă��܂��B����ŊO�p�̘a�Ɋւ�����ł͓ʑ��p�`���Ƃ����������Ȃ���Ă��܂��B���w���w�ł́A�Ƃ��ɒf�肪�Ȃ��ꍇ�A�P�Ɂu���p�`�v�Ɩ�蕶�ɏ�����Ă���Γʑ��p�`�̎����w���Ă���ƍl����悢�̂��A����Ƃ��O�p�̘a�Ɋւ�����̂݁A�����p�`�̊O�p�͍l���Ȃ����ƂɂȂ��Ă���̂ŁA���̖��̏ꍇ�̂݁A���p�`�Ƃ͓ʑ��p�`���w���ƍl���Ȃ���Ȃ�Ȃ��̂��A�A�A���܂��^��_���`�����Ȃ����ǂ�����������̂ł����A���w�����肢�������܂��B
�����m��ҁn�F�A�����肪�Ƃ��DK�Ђ̏ꍇ�C�{���ł͂Ȃ����߂Ɂu���̋��ȏ��ł́C�ꕔ�����ڂ��̂́C���p�`���珜�����Ƃɂ��܂��v�Ə�����Ă��܂��D�������C���`��u�[�������`�̖��������Ղ�Əo�Ă��܂����C����́u�E�̐}�ť���v�Ə����悤�ɂȂ��Ă��܂��D���Ђ̋��ȏ��ł́C�����I�ɂ͏�����Ă��Ȃ��悤�ł����C���ۏ�͑��p�`�Ƃ����p�ꂪ�����p�`��\�����Ƃ͂Ȃ��悤�ɏ�����Ă���悤�ł��D�i�O�p�Ƃ͊W�Ȃ��C�O�p�`�C�l�p�`�C�܊p�`�C����C���p�`�ƌ����Γʐ}�`�݂̂�\�����C���}�`�́u�E�}�̥���v�Ƃ����悤�ɐ}�����Ă���Ƃ������Ƃ炵���ł��j�D
�@���̗��ꂩ�猾���C�Ⴆ�u�l�p�`�̓��p�̘a��360���ɂȂ邱�Ƃ������Ȃ����v�Ƃ������ɑ��āC���k���ʎl�p�`�̏ꍇ�����ɂ��ďؖ����s���C���l�p�`�̏ꍇ�������Ă��Ȃ��Ă��C���_�Ƃ������Ƃ��ƍl�����܂��D
���m�ʂ̕ł���̎���ɑ���n[�����i�S����,����,�����j�ɂ��ā^23.08.10
60l�́A��l��75���ł����B
�����m��ҁn�F�A�����肪�Ƃ��D�͂��߂ɁC�t�̗̂e�ς�\���L�����b�g�����C�A���t�@�x�b�g�������̃G��(l)�ŏ����ƁC�����̃C�`(1)�ƕ���킵���̂ŁC�ŋ߂̋��ȏ��ł̓A���t�@�x�b�g�啶���̃G��(L)�ŏ������Ƃ������D�M�L�̂̃G��(
ℓ)���悭�g����D�������C�A���t�@�x�b�g�̕M�L�̂͏����Ȃ��Ă��悢�Ƃ�������ŋ�����ꍇ�ł��C���w�ł�
a��
x���u���b�N�̂ŏ������Ƃ͂��Ȃ��D��
a, x�͕K���M�L�̂ŏ����D
ℓ�͕M�L�̂ŏ������C�܂���L, mL�̂悤�Ƀ��b�g���̕�����啶���ŏ����D
�@����̌��F
60=0.75x→

(
ℓ)
���̕����ƕ����̊Ԃ��Ă��Ă킩��₷�������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�S�����i�p�[�Z���g�j�ɂ��ā^23.07.26
0.012�����ɖ߂�����
�����m��ҁn�F�A�����肪�Ƃ��D���ނ�ǂ�ł���C���₪����Γ�����Ƃ�������ɂȂ��Ă��܂����C���ނ�ǂ܂��Ɏ��₵�Ă��܂��H��Ƃ��āC0.03=3%, 0.12=12%, 0.8=80% �������Ă���܂����C��������āC0.012�����ɖ߂����@��������Ȃ��Ƃ�����������Ă���̂ł����H
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝(�������)�ɂ��ā^23.07.25
�V�w�K�w���v�̂ɂ��ƁA�~���p�͒��w3�N���ɁA�����̎��ɗ��C����ȖڂɂȂ��Ă��܂��B
���̂܂܂ł��\�����Ƃ͎v���܂����A�������Ă���������ƍK���ł��B
��肪�ǖ⑵���Ŋ�b�͂����܂��Ă���̂��������Ă��܂��B���ꂩ�����낵�����肢�������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�w�N�i�s�ŕς��̂ŁC2�N�ɂ�����̂�3�N�ɂȂ�ꍇ�C�����������邩�����Ă��邤���ɥ�����������܂����D�������C�T�u���j���[�̏�[�̊w�N�\���́C�u���E�U�̃L���b�V���@�\�̂����ŁC�ȒP�ɂ͕ς��Ȃ��悤�ł��D
�� �m ? /�������������^23.07.06�n
���݂V�T�{�P�h�~�Ƃ��Ċ撣���Ă���܂��B
���w�̓{�P�h�~�Ƀx�X�g�ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���s���Ɗp ==�i���K���2�j�ɂ��ā^23.06.24
��萔�𑝂₵�ė~�����ł��B�i���w2�N���ł��j
�����m��ҁn�F�A�����肪�Ƃ��D���̖����܂߂āC���̍��ڂɂ�17��قǂ���܂����i�ڎ��Q�Ɓj�C���s���Ɗp�̍��ڂ����ŁC����ɂ����Ƒ��₵�Ăق����Ƃ����v�]�Ƃ��Ďt���܂����D�������ȓ��Ɏ�������悤�ɂ��܂��D
���m�ʂ̕ł���̎���ɑ���n[�f���������̉��p�ɂ��ā^23.06.24
����(4)�̂����������Ă��������B���肢���܂��B
�����m��ҁn�F�u�ǂ̂悤�Ȑ���������悢���E������I�тȂ����v�Ə����Ă���̂�����C�E������I��=�N���b�N����̂ł��D�u�N���b�N����C����Ɖ��\������܂��D���Ă��邾���ł́C��������\������܂���v�D�i�{�j
���m�ʂ̕ł���̎���ɑ���n[���������ɂ��ā^23.06.18
��łƂ���()�Ƒł̂���Ԃ�������̂łق����̂������Ⴆ��[]�Ȃǂł������ɂȂ�悤�ɂ��Ăق����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�� -- ( )��{ }, [ ]�Ȃǂ͐��w�ł��R���s���[�^�ł��C���ꂼ��ʂ̖������^�����Ă���̂ŁC���ڂ������܂��ɂ��邱�Ƃ́C��ōГ�������\������D
���m�ʂ̕ł���̎���ɑ���n[�f���������̉��p�ɂ��ā^23.06.13
�f�������������邱�Ƃłł���悤�ɂȂ邱�ƂƂ͂Ȃ�ł����H
�����m��ҁn�F�A�����肪�Ƃ��D���w�Z�̐��w�̋��ȏ��Ō����C��1�́F�������i���̌v�Z�j�C��Q�́F�������̏��ɏ�����Ă�����e�̂����ŁC�������̏͂őf���������������̕����̖�肪�ł���悤�ɂȂ�܂��D
�@�����ɂ������Ƃł����C����̗L�����Ȃǂ̌ォ��K�����Ƃ��ɋ����邱�Ƃ͖����ł�--��x�ɑS���������ƂɂȂ邩��D������C���ȏ��̖ڎ��ŁC���̍��ڂ�����ɏ�����Ă��邱�Ƃ��w�Ԃ��߂ɕK�v�ɂȂ�܂��Ƃ����ׂ���������܂���D
�@�Љ�l�����ɂ́C�Ⴆ�CExcel�̂��鑀����@��������Ƃ��Ɂu���̋Z�p���w�ׂC�Z�Z���ł���悤�ɂȂ�܂��v�Ƃ����`�ŁC�ڕW�������Ċw�K�ӗ~�Ɍ��т���Ƃ������Ƃ́C�L���s���Ă��܂��D�������C���w�̊w�K�̂悤�ɁC���������K���Ă��Ȃ������������Ӗ�����̂���O�����Đ�������͖̂����ȏꍇ���قƂ�ǂł�����C�O�����Ĉꗗ�\�ɂ��邱�Ƃ͂ł��Ȃ��̂ŁC�C�ɂȂ���͖ڎ������Ă��������Ƃ��������e�ɂȂ�܂��D
�@�f�����������ł���C�C���C���ł���悤�ɂȂ�C�{���C���{���C�ʕ����ł���悤�ɂȂ�܂��C����������̕�������I�m�ɏ����ł���悤�ɂȂ�܂��C�Ƃ������������ł��܂����C����͍����Ă��鑤�ʂ�����C�����Ă��Ȃ����ʂ�����C�ӗ~�t���ɂ͂Ȃ肦�܂����C���w���͑f�����������K��Ȃ��Ă��C�C�ʕ����ł��邱�Ƃ��l����C���̐����͐��m�ł͂Ȃ��Ƃ������܂��D
���m�ʂ̕ł���̎���ɑ���n[�P�����̃O���t(�ؕЂƌX��) �ɂ��ā^23.06.12
https://www.geisya.or.jp/~mwm48961/math/m2line04_2.htm
��f�y�[�W�����́u���j���[�ɖ߂�v�����N�� href �����l�� "math/index_m.htm" �ƂȂ��Ă���A�N���b�N�����
https://www.geisya.or.jp/~mwm48961/math/math/index_m.htm
�֔��ł��܂��i"math" ��1�����j Not Found �ƂȂ�܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂����D
���m�ʂ̕ł���̎���ɑ���n[HTML�̊�{(1)�ɂ��ā^23.06.10
�L�������܂�❣️�y�����v���O���~���O�����ėǂ����ɂȂ�܂����B���̊w�Z�ɂ��A���p���ė~�����̂Ő���F������Q�����Ă݂ĉ������I�I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���ލ����܂Ƃ߂��ɂ��ā^23.06.03
7x�|x=7? �� x�����Ƃ͂����������Ƃł͂Ȃ��A�H�̕��������̈Ӗ��Ȃ̂��킩��ɂ����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�u�~�͋��Ȃ̂��H����Ȃ͂��͂Ȃ��v�Ƃ����ꍇ�Ɓu�~�͋��ł͂Ȃ��v�Ƃ����ꍇ�ł́C�����̕����͓����ł��C�~�͋���������Ȃ��Ǝv���Ă���l�������p���ēǂ߂鎞�Ԃ��Ⴄ�D�^�╄�ň�U�����p���ƁC�����ōl���鎞�Ԃ��ł��饥����ʂ�������C��ɕt���C�ǂݔ���ӏ��ŗ����~�܂邱�Ƃ́C�����Ӗ����Ă���̂��D����́C������������Ȃ��Ƌ^���Ă���l�ɈӖ�������D
���m�ʂ̕ł���̎���ɑ���n[�A���������i���Z�������j�ɂ��ā^23.06.02
���肪�Ƃ��������܂�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�u�������ɂ����������ɂ��ā^23.05.30
����̏o����e�Ɖ���v�̂͑��̗��Ɖ���Ƃ͔�r�ɂȂ�Ȃ��A��ϗǂ�������₷�������ł�
�[���ł�����e�ł����B���̉�����e�͊w�ԑ��̗����ʒu�łȂ��A�����Ă�鑤�̗����ʒu
�ƂȂ��Ă���厖�ȂƂ��낪�����Ă��荡������o�Ȃ��܂܂ƂȂ��Ă��܂����B
��ώQ�l�ɂȂ�܂����A�L��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�H�����̔Z�x�ɂ��ā^23.05.09
�����A��Ƃ̈�ʋ��{����������܂��B21�ɂ��ĎZ�����ł��Ȃ��ł��B��������ď����ł�������悤�ɂ��܂��I
�����m��ҁn�F�A�����肪�Ƃ��D�A���Ƃ������Ƃ���
���m�ʂ̕ł���̎���ɑ���n[�t���Ɗ���Z�ɂ��ā^23.05.06
��葝�₵�Ăق����B
�����m��ҁn�F�A�����肪�Ƃ��D��萔��16�������̂ť���ʏ�u�������I�v�Ƃ����ꍇ�́C�O�����ɂ��C���N�������Ƃ������ƂŁC�悢���Ƃ��Ȃƥ��
���m�ʂ̕ł���̎���ɑ���n[�P�����Ƒ������ɂ��ā^23.05.03
�Ƃ��Ă��킩��₷�������ł��B
�ȒP�Ȗ�肪���Ă���̂ł����Ɨ����ł��Ă���̂����������Ă悩�����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���R�܂Ƃ߂̃`�F�b�N�iNo.6�j�ɂ��ā^23.05.02
�]�g���ɂƗ��p�����Ă��������Ă��܂��B���Ɖ����v���Ă��Ȃ��Ǝv������̂�����܂����̂ł��m�F���������F���R�܂Ƃ߂̃`�F�b�N�iNo.6�j�A2�y�[�W�ځy �ω��̊��� �z��(5)
�����m��ҁn�F�A�����肪�Ƃ��D��������₱�����̂ł����C���̖��͂��̌W�����Œ�I�ɏ�����Ă���̂ł͂Ȃ��C������p���Ė���قȂ���Ɖ��o�����悤�ɂȂ��Ă��܂��D���̏ꍇ�ɁC1000��`�������W���āC�����₷���W���̑g�ݍ��킹�ɂȂ�Ȃ��Ƃ��ɁC���炩���ߗp�ӂ����f�t�H���g�̒l���o���d�g�݂ɂ��Ă������̂ł����C�u�R���}�v�P�̏��������ŁC���܂��쓮���Ă��܂���ł����̂ŁC�������܂����D�J��Ԃ��ɂȂ�܂����C���x���Ă��������Ă��������͏o�܂���̂ŁC�����ł������ǂ����́C���Ɖ�����C�̐������݂̂Ŕ��f���Ă��������D
���m�ʂ̕ł���̎���ɑ���n[ �P�����Ƒ������ɂ��ā^23.05.01
�|�C���g�ȂǏ����ė~����
�����m��ҁn�F�A�����肪�Ƃ��D�����ɏ����Ă���̂��|�C���g�ł��H�H
���m�ʂ̕ł���̎���ɑ���n[�f���������̉��p�ɂ��ā^23.04.30
�������ǂ��ɂ��邩�킩��Ȃ������̂ŕ�����₷���\�����Ăق����ł�
�����m��ҁn�F�A�����肪�Ƃ��D�������Ă��邾���ł͉͏o�܂���D�u�E�������I�ׂv�̓_���ʂƉ�����o�܂��D
���m�ʂ̕ł���̎���ɑ���n[�A���������̕��͑�2�ɂ��ā^23.04.30
���1-4(1)�̒��Ł~180�ƂȂ��Ă܂����~100�ł͂Ȃ��ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��D��蕶��180g�ƂȂ��Ă��邩��C�~180�Ƃ������Ƃł�
���m�ʂ̕ł���̎���ɑ���n[�a�Ɛς̈��������ɂ��ā^23.04.25
�ς�-18�a��-7
�����m��ҁn�F�A�����肪�Ƃ��D�e���̏h��Ȃǂ́C�e���ł��܂��傤�D�Ȃ��C
���̃y�[�W�̉��̕��ɉ����Q�l�ɂȂ肻���Ȃ��Ƃ����
�ƂĂ�������₷���A�Q�l�ɂȂ�܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���s���Ɗp(���K���2)�ɂ��ā^23.04.22
����Ȋ����̖���T���Ă����̂ŏ�����܂����A�I������킩��₷���Ă��肪�����ł��B���̖����Q�l�ɁA�e�X�g���撣��܂��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���Ώ̂Ȑ}�`�ɂ��ā^23.04.21
���肪�Ƃ��������܂����B
���ɗ����܂���
���P�_�͂�蒼���͂���Ȃ��Ǝv���܂�
�����m��ҁn�F�A�����肪�Ƃ��D1��ŕK�������ɂȂ�Ƃ������Ƃ��ȁH
���m�ʂ̕ł���̎���ɑ���n[�������ɒ������K�ɂ��ā^23.04.04
�ƂĂ��킩��₷����肪������悤�ɂȂ�܂����B
����������낵�����肢���܂�❗️���́A�����������ɒ������������Ă��������B���҂��Ă��܂�❣️
�����m��ҁn�F�A�����肪�Ƃ��D��??�u�����������ɒ����v�ł����C�������ɏ����Ă����ˁD
���m�ʂ̕ł���̎���ɑ���n[�������̍��� �ɂ��ā^23.03.20
�������킩��₷���A�ƂĂ��������Ă��܂��B���肪�Ƃ��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�s�����̉������ɂ��ā^23.03.20
�ƂĂ��f���炵��
�����m��ҁn�F�A�����肪�Ƃ��D����ے��̉����ɂ����Ԃ��ł��āC�P���s�������\���K���Ȃ��������オ�������悤�ł�
���m�ʂ̕ł���̎���ɑ���n[���Ώ̂Ȑ}�`�ɂ��ā^23.03.19
���₷�������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�H�����̔Z�x�ɂ��ā^23.03.18
��������������₷���i�r�[�J�[�}�Ȃǁj�����������������Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�����Ă�����̂��C�����������悢�ƌ����Ă��˂��D
���m�ʂ̕ł���̎���ɑ���n[�s�����̉������ɂ��ā^23.03.18
�w�Z�ł��m�ł��K��Ȃ������͈͂ʼn��������킩�炸�����Ă����̂ŏ�����܂����I
�������̉�����������Ƃɖ�肪���x���ʂɂ����Ă킩��₷�������ł�
���肪�Ƃ��������܂���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������̑召��r�ɂ��ā^23.03.15
��قǖ��S�̓����ԈႦ�Ă���̂ł͂Ȃ����Ƒ��M�������̂ł��B
�����������ԈႢ�Ă��܂����B
�y���Ȕ��f�ő��M���Ă����܂��A�\����܂���ł���
�����m��ҁn�F�A�����肪�Ƃ��D�����ł�
���m�ʂ̕ł���̎���ɑ���n[�������̑召��r�ɂ��ā^23.03.15
���S�̉��A�G,�C,�E,�A�ɂȂ��Ă��܂����A�������́A�G,�E,�C,�A�ł͂Ȃ��ł��傤���H
�d��Ōv�Z���Ă݂��̂ł���
�A���Q�D�W�W�U�E�E�E
�C���Q�D�Q�R�U�E�E�E
�E���P�D�R�S�P�E�E�E
�G���O�D�R�S�U�E�E�E
�ƂȂ�܂���
���P��낵�����肢���܂�
�����m��ҁn�F�A�����肪�Ƃ��D
���Ȃ��́C(�C)��

�Ƃ��Ă��܂����C���́C

�Ȃ̂ŁC���Ȃ��̓ǂ݊ԈႢ�ł��D
x = 3 �̂Ƃ��C 2 x + 4 �̎��̒l�����߂Ȃ����B
�����m��ҁn�F�A�����肪�Ƃ��D���T�C�g�ł́C�h���s�Ƃ͂���Ă��܂���D���͂���ChatGTP�ɏ������߂C���͏o�Ă���ł��傤�D
���m�ʂ̕ł���̎���ɑ���n[��������iNo.1�@�a���^���ʕ���j�ɂ��ā^23.03.08
�������������̎��̊��郋�[���ɂ��Ē��ׂĂ��Ă��̃T�C�g���������̂ł����A���̕��K�Ƃ��Ė�肪����̂��ƂĂ����ɗ����܂����I�ł����A�v�Z�̓�����Ƃ��Ƀ{�^�����������ĉ����Â炢�ł����B
�����m��ҁn�F�A�����肪�Ƃ��D�R���s���[�^�̎g�����́C��҂��V�l�ɋ�������̂Ƃ����̂��C���ʂ̗���ł��������ʂ��g�傷��ɂ́CWindows�n�̃p�\�R���ł́uCtrl+(+)�v�C�X�}�z�ł́u�s���`�A�E�g�v�i��{�̎w���L����j�łł���悤�ł��D
���m�ʂ̕ł���̎���ɑ���n[�P�����Ƒ������ɂ��ā^23.03.06
�։�̏��ɕ��ׂ鎞�A�~�ׂ��̏��͖����ł��܂����H�܂��A���������̎��A�`���[�g�̗��ŗ։�̏��̓����ɂȂ邱�Ƃ������ł����A�~�ׂ��̏��ʼn��Ă��ۂ͖Ⴆ�܂����H
�����m��ҁn�F�։��Ƃ����p��́C�C���h�n�̓Ɠ��̐��E�ςŁC���w�Ŏg����̂��֊��̏��Ƃ����܂��D
�@����������W�J�̓��ẮC�Ȃ�ׂ��~�ׂ��̏��ɏ����C���������������́u�֊i�T�C�N���b�N�j�̏��v�܂��́u�������z��i�A���t�@�x�b�g���j�v�ɏ����̂����₷���ł��傤�D
�@���̃y�[�W�ɂ������Ă��܂����C�P�̕����ɒ��ڂ���u�~�ׂ��̏��v�����₷���C�Q�ȏ�̕�����Γ��Ɍ���ꍇ�́C�ǂ̍���2�����ł���悤�Ȏ��̂悤�ȗ�ł́C�~�ׂ��̏��Ƃ����Ă����ׂ悤���Ȃ��ł��傤�D
�֊̏�→a2+b2+c2+ab+bc+ca
�������z��→a2+ab+ac+b2+bc+c2
�@�b����₱�����ł����C�֊̏��Ƃ������Ƃ�������̂́C�R�����̏ꍇ�����ŁC�S�����̏ꍇ�ɁCab+bc+cd+da�Ə�����ac+bd�̏����ꏊ���Ȃ��Ȃ�̂ŁC�������z��ab+ac+ad+bc+bd+cd�̕����l�X�ȏꍇ�ɑΉ��ł���ł��傤�D�����R�����̏ꍇ�Ɂu���₷���v�u�_�����₷���v�u���Ԃ̏펯�ɍ��킹�₷���i���W�̉ƍ��킹�₷���j�v�̂͗֊̏��ł��傤…�Ⴄ���œ��Ă��������Ƃ��ɁC�~�ɂ���悤�ȓ��e�ł͂Ȃ��ł��傤�D…�����C�u�����v���d������^�C�v�̐搶���Z���̒�������ȂǂŌ��_���邱�Ƃ͂��邩������܂��C����ł���_�ɂ͂��Ȃ��ł��傤�D
���m?���^��������^23.03.05
�����ȋ^����A������Ăق�����
�����m��ҁn�F��������k���Ƃ������Ƃ��������Č����Ă����ˁD���̋^��̒��g������Ȃ���Γ����Ȃ�
���m�ʂ̕ł���̎���ɑ���n[�_�Ώ̂Ȑ}�`�ɂ��ā^23.02.26
�Ⴄ�Ƃ���́A�Ȃ��Ⴄ�̂��̐}�����Ă�����A�|�C���g��������Ă����̂ŁA�ƂĂ��킩��₷�������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D����Ȃ�ɋ�S�̍�Ȃ̂ł�
���m�ʂ̕ł���̎���ɑ���n[�O�����̒藝�A���̂̑̐ρE�\�ʐ��ɂ��ā^23.02.23
�������킩��Ȃ��ł��c
�����m��ҁn�F�A�����肪�Ƃ��D�̃{�^����t���܂���
���m�ʂ̕ł���̎���ɑ���n[���ʊp�C���p�C�O�p�`�̓��p�̘a�C�O�p�̗��K����ɂ��ā^23.02.23
�i�R�j �ł́A����m�An�ɑ��鐂�����A45�x���Ȃ��_��ʂ�悤�Ɉ����Ǝl�p�`�ƎO�p�`���ł���̂ŁA�����̓��p�̘a�𗘗p���ĉ����܂������A����̕����v�Z�����Ȃ��ł��ˁB
�}�`���̓Z���X�����Ă���C�����ċ��ӎ��������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝(�������) �ɂ��ā^23.02.19
�ƂĂ��ǂ����Z��ɂȂ�܂����B�O�����̒藝�̉��p��ꎟ���Ɠ��̗Z�����̉��p�ȂǁA�ō����_��_�����߂̃v�����g������Ă��炦��Ƃ��肪�����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
�ڎ������Ă��炤�ƁC�O�����̒藝�̉��p��ꎟ���Ɠ��̗Z�����̉��p�Ȃǂ�����܂��̂ŁC�����������Ă��������D
2�Ԃ̓������Ԉ���Ă��܂��B66�ł͂Ȃ��A72����Ȃ���ł����H
�����m��ҁn�F�A�����肪�Ƃ��D?? �\�ʐςƑ̐ς̈Ⴂ�𗝉����Ă��܂����H
���m�ʂ̕ł���̎���ɑ���n[�s�����̉������ɂ��ā^23.02.16
�Q�l�ɂȂ�܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�S�����i�p�[�Z���g�j�ɂ��ā^23.02.16
���ɗ�����
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�P���������̉������ɂ��ā^23.02.13
�ƂĂ��킩��₷��!���ꂩ����Q�l�ɂ����Ă��������܂��B���肪�Ƃ��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���Ώ̂Ȑ}�`�ɂ��ā^23.02.05
�ǂ��ł�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�P�����̕��͑��ɂ��ā^23.02.04
�����̃e�X�g���͊ȒP�����ǁA�����̉ߋ���ɌX�����ɂĂāA��Փx���������G�����ǁA�߂��������킯�ł��Ȃ����炢�̊����ŁA���傤�ǂ悩�����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�P���������̉������ɂ��ā^23.02.04
�܂����w�U�N���ł�������ł�������₷�����ł������ł��܂���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�O�����̒藝�̉��p�ɂ��ā^23.01.31
�ᕶ���킩��₷���A��b���牞�p�܂ł�������ł��Ă悩�����ł��B
���̃T�[�r�X�����Ɨ~�����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Q��C�������C���[�g�ɂ��ā^23.01.31
�킩��₷���ėǂ��ł��B�B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�O�����̒藝�A���̂̑̐ρE�\�ʐ��ɂ��ā^23.01.31
5�̐}�`�̒f�ʂ̐}��A��ʂȂǂ̕�����F�������Ă����āA�ƂĂ��킩��₷���ł��B
�����A~cm�Ȃǂ̕����̐F��Ⴆ�ΗΐF�ȂǐF����������������ƌ��₷���Ȃ邩�Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~�ɓ��ڂ���l�p�`�ɂ��ā^23.01.29
����������蕶���~�����ł�
�����m��ҁn�F�A�����肪�Ƃ��D���̎��̃y�[�W�����Ă�����������g�т̕��y�ɔ����āC�ڎ������Ȃ��l�������Ȃ��������C�Ƃ����v�����]�������饥�
���m�ʂ̕ł���̎���ɑ���n[�����Z�ɂ��ā^23.01.25
��57�ɂ��Ċ�b���o���Ă��Ȃ�������������y�[�W�ł�
�ڂ��V�l�ɂȂ�Ȃ��l�Ɋ��p���Ă��������ł�
���̒��ŋC���t�����̂����K���Ő�������ƑI�����������Ă��܂����ł�
�N���͉�����ǂݕԂ��Ȃ��ƑʖڂȂ̂ŁA����������ϐF��������x�ɂ����炢�����ł��傤���H
�����̂����ɗ��Ă�K���ł�
�����m��ҁn�F�A�����肪�Ƃ��D�B���������Ă�Ίw�K�ӗ~���ێ��ł���C�Ƃ������ƂŁC�i��������肪�����Ă����Ƃ����̂́C���܂ł悢�]���������ł��D���̃v���O�����́C������20�N���炢�O�CNetscape Navigator 3�i�l�X�P����Ɠǂށj���S�����������ɍ�������̂ŁC���������͊ȒP�ł͂���܂���D�Ȃ��C�u���E�U�̋@�\�Ƃ��čēǂݍ��݂��s���Ă��炦�C���Ɠ����̔z���ς��ĉ��x�ł��o�肳��܂��̂ŁC���̋@�\���g���Ă������������C�w�K���ʂ�����Ǝv���܂��D
�@�Q�l�C��҂����Z�̂���C���Ȃ��͂܂����܂�Ă��Ȃ������悤�ł��D�Y�����Y���|��̉��ɕԎ��������Ă���悤�Ȃ��̂ł�
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝�ɂ��ā^23.01.16
�����������x���̍�����������Ă���������Ɗ������ł�
�����m��ҁn�F�A�����肪�Ƃ��D�P�y�[�ɖڂ͂₳�����Ȃ��Ă��āC���̃y�[�W�ɐi�ނƂ����̂����ʂ̓ǂݕ��ł��D
���m�ʂ̕ł���̎���ɑ���n[�������ɒ������K�ɂ��ā^23.01.15
��2���3��N���b�N�o���邩��1��������I���݂����ɂ���Ηǂ��Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�Ԉ�������k�́C���̌�ǂ��Ȃ�̂��ȁH
���m�ʂ̕ł���̎���ɑ���n[�ڌ��藝 no.2�ɂ��ā^23.01.11
�l�X�ȓ�Փx�������ĂƂĂ��킩��₷���ł��I�ǂ�ł���Ă邩�킩��Ȃ����NJ��ӂ��`���Ƃ�����w
�����m��ҁn�F�A�����肪�Ƃ��D���̃y�[�W��PC�p�̉�ʂł��DiPhone�œǂނƕ������������Ȃ��ēǂ݂ɂ����̂ŁC�g�їp�̃y�[�W�i�擪�Ɏ����Ă���j��ǂޕ����悢�ł��傤�D
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝(�������)�ɂ��ā^23.01.11
����ł�
�����m��ҁn�F�A�����肪�Ƃ��D������肩��ǂݎn�߂������̂ŁC���̃y�[�W�Ɍ����Ă���T�u���j���[�̍ŏ��̕��̊�{��肩�����Ă��������D
���m�ʂ̕ł���̎���ɑ���n[�H�����̔Z�x�ɂ��ā^23.01.10
�ƂĂ��킩��₷�����������K���������č̓_�Ɖ�������Ă���Ď��ʃp�[�Z���g�Z�x�̉��������킩��܂����I�I���肪�Ƃ��������܂��I�I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�P�����̃O���t(�X��) �ɂ��ā^23.01.08
�����{�^���������ɂ��������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�g�т�PC�p�̋��ނ����܂��ƁC�c���䂪����Ȃ��̂Ō��ɂ����Ȃ�܂��D��ʂ̐擪�Ɂu�g�їp�v�Ƃ����K�C�h�����Ă��܂��̂ŁC����������Ă��������D
���m�ʂ̕ł���̎���ɑ���n[�O�p�`�̑��������ɂ��ā^23.01.05
�ؖ��̎d���̂�������킩��₷�������ł��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝(�������) �ɂ��ā^22.12.22
�����ƕ�����₷�����Ăق����B
�����m��ҁn�F�A�����肪�Ƃ��D������Ȃ��Ƃ����l���u������肩�珉�߂Ăǂ�����˂�v�Ƃ��������D�~���p�̒藝�̊�{��肪�ڎ��ɂ���܂�����C�������珇�ɂ��ƕ�����悤�ɂȂ�ł��傤����i����ȁC����ȁj
���m�ʂ̕ł���̎���ɑ���n[�������ɒ������K�ɂ��ā^22.12.21
�����͂ǂ������炢���ł���
�����m��ҁn�F�A�����肪�Ƃ��D�b���ʂ��܂���D(A)�u�����������ɒ����ɂ́C�ǂ�������悢�ł����v�C(B)�u�������ɒ����ɂ́C�ǂ�������悢�ł����v�̂悤�Ɏ��₷�ׂ��ł��D
(A)�̏ꍇ�C�Ⴆ�u������3�������_�ȉ���Q�ʂ܂ŏ������g���ĕ\���Ȃ����v�Ƃ����ꍇ�́C3.00�̂悤�ɂO��t�����������ł��D(B)�̏ꍇ�C�Ⴆ�u������3���ŕ\���Ȃ����v�Ƃ����ꍇ�́C������P�ɂ��ď����܂����

�@

�̂悤�ȁC�����܂݂̕����i�ѕ����j��(C)�u�����ɒ����ɂ́v�C5.66����̂悤�ɕ����̕����������ɒ����悭�C(D)�u�������ɒ����ɂ́v�Ƃ������̏ꍇ�́C

�̂悤�ɐ����̕�����Ɗ|���Ă��番�q�ɑ����܂��D
�}�C�i�X���ĂȂ�
�����m��ҁn�F�A�����肪�Ƃ��D���[���̃A�h���X��web�y�[�W��URL�Ƀn�C�t���i�}�C�i�X�j�̋L���͂�������g���Ă��܂��D���ꂪ���͂ł��Ȃ���C���E���ő呛���ɂȂ�͂��ł��D���Ȃ��́C�܂��㓙��iPhone���g�����Ȃ��Ă��Ȃ��Ƃ������Ƃ̂悤�ł��D�M�҂̂悤�Ȓʂ肪����̂�������ł����͂ł��܂�����L�����A�i�h�R��,AU,�\�t�g�o���N�Ȃǁj�̈Ⴂ�łȂ��āC�@��ɂ���ăX�N���[���L�[�{�[�h�̌��������Ⴄ�悤�ł����C�A���t�@�x�b�g���ɂ���ꍇ��A���t�@�x�b�g������ł�����������ł��������߂�ꍇ������܂��D1�~�Ŕ�����Google Pixel�ł�,���������Łu�}�C�i�X �S�v�͓��͂ł��܂������X�g���邱�Ƃł��̂ŁC�������̃X�N���[���L�[�{�[�h�ŁC�w�𗣂��O�ɏ㉺���E�ɂ��点��Z�p���K�����Ă��������D
���m?���^���[�܂���^22.12.14
�����Ɩ�萔�𑝂₵�ė~�����ł�
�����m��ҁn�F�A�����肪�Ƃ��D�ǂ̃y�[�W�̘b�Ȃ̂�������Ȃ��ƁC�b���ʂ��܂���
���m�ʂ̕ł���̎���ɑ���n[���ʐ}�`�̗p���ɂ��ā^22.12.14
�S�̓I�ɕ������������A�I�т����p��ȊO�̂Ƃ��낪�������Ă��܂��A���Â炩�����B
�����m��ҁn�F�A�����肪�Ƃ��DPC�p�̋��ނ�iPhone�œǂނ͖̂����ł�
���m�ʂ̕ł���̎���ɑ���n[�P���������̕��͑�i���ĕt:���j�ɂ��ā^22.12.14
��������̖��A�킩��₷�����肪�Ƃ��������܂�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����i�S����,����,�����j�ɂ��ā^22.12.13
52L�́A65L�̉����ɂ�����܂����H
�����m��ҁn�F�A�����肪�Ƃ��D�ŋ߂́C�h��̓�����������ƁC�ςȖ��Ɋ������܂�邱�Ƃ�����悤�ł��̂ŁC�q�˂��Ă�����̂Ƃ͕ʂ̖��ɓ����܂��D
�s��1�t28(m)��35(m)�̉����ł���→28��35=0.8������80% �s��2�t63(kg)��90(kg)�̉����ł���→63��90=0.7������70% �s��3�t39(L)��65(L)�̉����ł���→39��65=0.6������60%
���m�ʂ̕ł���̎���ɑ���n[�������ɒ������K�ɂ��ā^22.12.13
���傱���ƍl�������킩��₷������Ɨǂ��Ǝv���܂�
�ł������͗����ł��܂���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�m��(���Z�������)�ɂ��ā^22.12.12
��w�����ł��i���w�ł͂Ȃ��C�R���s���[�^�̐v�����ł��j�D�����̎q�����Љ�l�ɂȂ�����C�����ł������̂Ŗ��ɗ���������5�N�O���玙���{��{�݂Ŋw�K�{�����e�B�A�����Ă��܂��DDV��s�҂Ȃǂʼnƒ�ŕ��̊����قƂ�ǂȂ������q�������̂����C���w���E���Z���̐��w�𒆐S�ɁC���w�Z�̍H��Ȃǂ��w�����Ă��܂��i���݁C�T3��j�D���l���ł͂ł��Ȃ��q���������̂ŁC�ƒ닳�t�X�^�C���ł��D����̂��̃T�C�g�́C���w���Ŋw�K�ӗ~�������������C���łɋ��ȏ��͏I������̂ł����Ɠ����Ɏg����������������Ƃ����̂Ō������ĂƂĂ����ł��܂��D
�f�������ǁC��{�I�Ȍv�Z���ア�q���͏��w���ɖ߂��ĕ�����������Ă��܂��D���ɂ́C�悭�ł��鐶�k�����܂����C��ȂȎ��������܂��D�Ⴆ�C�L�q���ł͎����c���C���Z�������肷��Ƃ��Ɏg���邵�C�v�Z���M�Z�ł���̂Ȃ�����Ă͂����Ȃ��Ǝw�����C�̓_�҂͋L�q���͓r�����œr���_������邱�Ƃ������̂ŁC�c�����ق����ǂ��Ƃ����Ă��Ȃ��Ȃ��������Ƃ������Ă���܂���D�L�q���œ_������邽�߂̔錍�Ȃǂ����̂悤��Web�T�C�g�ōڂ��Ă����ƁC�q���Ɏ���Ă�Web�T�C�g�Ō��J���ꂽ���͐M������X���ɂ���̂ł��ꂵ���ł��D
�����m��ҁn�F�A�����肪�Ƃ��D���̃��x���ł��C���ʃe�X�g�ō��ݓ������L�q����������ɂ͎����Ă��Ȃ��悤�ł��D�e�w�Z�̒�������̃��x���ŁC���ׂȖ��܂ō��ӂł���W�c�̒��Ȃ�\��������܂��C�s���{���P�ʂ̓��w�����ȂǂŁu���Ă̏����J�v���v������鎞��ɁC���̈Ӗ��������ł��Ȃ��ی�҂��P���l�ɂP�l�ł�����\��������Ȃ�C�L�q�����Ăɓ��ݐ邱�Ƃ͑����ȃ��X�N������܂�����ڋ߂ȗ�Łu�~���p�͒��S�p�̔����ɂȂ邱�Ƃ��ؖ����Ȃ����v�Ƃ��������o�����Ƃ��Ɂu����́C�������D�Ȃ��Ȃ�C���ȏ��ɂ��������Ă��邩��v�Ƃ������Ă��_�ɂ����睆�߂�ł��傤�D�܂��u�~���p�͒��S�p�̔���������v�Ƃ������Ă��_�ɂ��Ă����߂�ł��傤�D���������u���Ăɂ͉��������Ȃ���Ȃ�Ȃ����C���������Ă͂����Ȃ��̂��v�Ƃ������Ƃ́C���x�ɎЉ�I�Ȑl�ԊW�̒��Ō�����\���ŁC�u���ނ肪���Ȃ邩�v���x���̑f�p�Ɏ��݂��镨�̘b�ł͂Ȃ��̂ŁC���k�ɂ��ی�҂ɂ��C�����L�q���ׂ��Ȃ̂��������ł��Ă��Ȃ����Ƃ����肦�܂��D���݂̓��ʎx������Ɉڍ�����O�́C�����̏��߂̍��ɁC���ʍZ�Ɨ{��w�Z�̌𗬂��s���ۂɁC�{��w�Z�̒S���̐搶���玖�O���N�`���A�Ƃ��āC���Ȃ�Z�������炷��ł��Ă��C�Љ�W�͍��x�߂��ė����ł��Ȃ����Ƃ�����Ƃ���ꂽ���Ƃ�����D���������Ӗ��ł́C���w�́i�ȒP�ȓT�^�I�ȁj�L�q���C�ؖ����ɑΉ��ł���\�͂́C�P�����I�ɕ�����Ȃ�u���Ύ����x���v�C�Q�����Ȃ�uA���Z�N���X�v�uB�����N���X�v�̂悤�Ȍ���������C�������ɂ��ċ����̒����̐i�������邩������܂���D
�@�Z���E���w�ɂ��ẮC�搶������s���̏ꍇ�����蓾�܂��D�ڋ߂ȗ�Ƃ��āC���w�Z�̗�Łu5�Ŋ����Ă��C7�Ŋ����Ă��C3�]���ԏ����Ȑ����͉��ł����v�i���F���w�Z�ɂ͕��̐��͂Ȃ��j�Ƃ������ɑ��āC�q�����u3�v�Ɠ����āC�~����������ꍇ�C�e=�������w�Z�̐搶�ɁC�����y�i�����X�^�[�y�A�����g�j�Ƃ��ċ��������Ă����ʂ�z�����Ă��炢�����D���w�Z�̐搶�́u3��5�Ŋ���Ȃ��v�ƌ����o���̂ł��D�����y�̎����u0�ȊO�Ŋ���Ȃ����͂Ȃ��v�Ƃ����̂ł����C�q���̗��ꂪ�܂����Ȃ��Ă͂����Ȃ�����C�K���Ɉ����������āC���w�Z�̎Z���͐�勳�Ȃɂ��ׂ����ƍl���Ă��܂��̂ł��D
���m�ʂ̕ł���̎���ɑ���n[���E���̐��̘a��(�������)�ɂ��ā^22.12.11
�y���������ł��B���肪�Ƃ��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝�ɂ��ā^22.12.11
�~���p��180���Ă��肦���ł���
�����m��ҁn�F�A�����肪�Ƃ��D�~���p�͒��S�p�̔����Ȃ̂ŁC�~���p��180���ɂȂ�Ƃ��́C���S�p��360���ƂȂ��āC�O�p�`���`���܂���̂ŁC���w�Z�ł͉~���p��180���Ƃ������Ƃ͂Ȃ��ł��傤�D��w�ł́C�w���w�Ȃɂ���ẮC���邩������܂���w�́C�P�X���I�܂ł͋�Ԃ̉Ȋw�ł������C�����I�ɂ͒�`�Ȃǂɂ���Č��܂���̐��E�Ȃ̂ť��
���m�ʂ̕ł���̎���ɑ���n[�������̍����ɂ��ā^22.12.10
���肪�Ƃ��������܂��B������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������ɒ������K�ɂ��ā^22.12.08
�������ɒ������K�i�����ł͂Ȃ��j�́C�ŏ��ɏ����Ă���܂��H
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������g�������ɂ��ā^22.12.08
�o�������ĂƂĂ�������₷������
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�s�����̉������ɂ��ā^22.12.08
�ƂĂ��悩�����ł�❗
�w�Z�ŏK���Ă��Ȃ��āA���[�N�̖��ɂ������̂ŗ��K�ł��܂����B
���������A��萔���ق��������ł�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���Ώ̂Ȑ}�`�ɂ��ā^22.12.08
�������ǂ�����
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[��`�̖ʐ��ɂ��ā^22.12.06
������ɂ����ł��B
��̓I�Ɍ����ƁA������Ƃ����̂��������킩��Ȃ�
�����m��ҁn�F�A�����肪�Ƃ��D�|������́C�킩��Ǝv���D����̕��́C���Ə����ꍇ�ƁC�����̕���ɏ����ꍇ�Ƃ������āC�����Ӗ��ł�
���m�ʂ̕ł���̎���ɑ���n[���E�����i�������j�ɂ��ā^22.12.06
������߂����ᕪ����₷���B
�ł������Ɠ����肪�~���������ł��c�c�c
�����m��ҁn�F�A�����肪�Ƃ��D������肾����C���ۂɏo�肳�ꂽ���̂����Ȃ��Ƃ������Ƃł�
���m�ʂ̕ł���̎���ɑ���n[�������̕��͑�i���m���̑I�ѕ��j�ɂ��ā^22.12.05
���1-4(1)�`�n�_����a�n�_�܂ł̋�����x���Ƃ��āCx�̕����������ƁC���̂����ǂ̎��ɂȂ�܂���
�̉́A
X�{�i�P�O�O�~�P�O�j/�P�O�O��X-�i�W�O�~�T�j/�W�O
�ł͂Ȃ��ł����H
�����m��ҁn�F�A�����肪�Ƃ��D�������̕��͑�������Ƃ��ɁC�����܂��ȕ��͋C��������Řb��i�߂�Ǝ��s���܂��D���ɁC�u�����v�u���Ɂv�������̂��Ƃ������Ƃ��u�P�ʁv�ɒ����čl���邱�Ƃ��d�v�ł��D�Ƃ���ŁC���Ȃ��̓��Ăɂ�X�������Z�E�܂��͈����Z�Ƃ��ēo�ꂷ��̂ŁC���ӂ͒����̒P��(m)�ŏ�����Ă��邩�H�Ɛq�˂Ȃ���Ȃ�Ȃ��D����100(m)��(100+10)/100�́C���������������璷���̒P�ʂɍ���Ȃ��̂ŁC���̑����Z�͂ł��Ȃ����ƂɂȂ�܂��D
���m�ʂ̕ł���̎���ɑ���n[���s���Ɗp�ɂ��ā^22.11.30
�ƂĂ��ǂ����ł����A���肪�Ƃ��������܂����I�ł����A��������͂���Ƃ�������̃L�[�{�[�h�ɕς��Ȃ��Ƃ����Ȃ��̂��������������������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�X�}�z��^�u���b�g������͂���ƁC�L�[�{�[�h���o�Ă��܂��D���͂��Ȃ����@�Ƃ��Ă͑I����������܂��D����܂���ł�������Ƃ����������������āC�꒷��Z�ł��D�����I�ɂ́C�I�����̕����ǂ������ł���
���m�ʂ̕ł���̎���ɑ���n[���s���Ɗp�ɂ��ā^22.11.30
�ƂĂ��A������₷�������ł��B���ɁA������������Ԉ���Ă������ɏo�Ă���̂ł͂Ȃ��u����v�̃{�^���������Ȃ��Əo�Ă��Ȃ��Ƃ��낪�ǂ������ł��B�i�悭�A�ԈႦ��Ƃ����ɓ����Ɖ�����o���T�C�g������̂ł��������ł������`�������W���������ɓ����łĂ��ĉ����C���Ȃ��Ȃ��Ă��܂���ł��B�j�e�X�g���߂������萔�w�̐}�`��肪�S�z�������̂łƂĂ��A������܂����B�{���ɂ��肪�Ƃ��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�H�^���C����^22.11.23
���w�ō��W���S�z�ŐF�X�ȃT�C�g�����ĕ������Ă�����ł���
�����̃T�C�g�̂悤�Ɏ��ۂɖ����������Ƃ��o�����A
����������Ǝv���������m�[�g�Ȃǂɏ����ʂ��Ƃ������Ƃ����o���Ȃ�
���I�ɓ��ɓ���ɂ����ʂ�����܂����B
�ł��������̃T�C�g�͎��ۂɂ��̏�Ŗ��������A���̌�ɓ������킹�A
�ԈႦ�₷���ꏊ��������Ă��ē��ɓ���₷�������ł��B
���I�ɂ͗ǂ��o�����X�̖��̓�����Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���W���_1�ɂ��ā^22.11.23
��̂̂������������n�͎��B�����ۂɂ����Ă��Ƃ��o�����A
�������͂�ǂ�Ńm�[�g�ȂǂɃ����̂悤�Ȋ����ŏ����Ƃ������Ƃ����o���Ȃ���
���I�ɂ͓��ɓ���ɂ����ʂ�����ς肠�����̂�
���������T�C�g�Ŏ��ۂɖ��������ē������킹���o����̂͗ǂ��ȂƎv���܂����B
���肪�Ƃ��������܂�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���Ώ̂Ȑ}�`�ɂ��ā^22.11.23
�ƂĂ��y�������ނł��A���ɂ��Њ��߂܂��B���ꂩ������e���[�������Ă���������Ɗ������ł��B
�X�������肢�v���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m?�^�x�W�[�^����^���w���n�^22.11.22
�s�����̎���ł��B
�����̓������ς��̂͂Ȃ��ł��傤���H
(��)7+2x<5x -6
��x>3/13
�����m��ҁn�F�A�����肪�Ƃ��D���Z�̐搶�ɁC���Z�̋��ȏ��͓���ł��܂����C���w�Z�̋��ȏ��͓���ł��܂���D����͂Q�̗v�f������ł��܂��D�P�ɂ́C�`������i�K�i���w�j�̋��ȏ��͖����Ȃ̂ŁC���w�Z�̐搶�ƒ��w���ɂ͕����Ȋw�Ȃ̔�p�Ŕz�z����܂����C���Z�̐搶�ɂ͌��{�ł���z�z���邱�Ƃ͂ł��܂���D�i���w�Z�̐搶�Ɍ��{���������Ƃ��肢�������Ƃ�����܂����u��ɓn���Ȃ��v�ƒf��ꂽ�j2�ڂ́C���ȏ��͕��ʂ̏��X�ł͓���ł����C���ȏ���舵�����X�ł̂ݔ̔�����Ă���Ƃ������Ƃł��D������C4������5�����炢�̓K���Ȏ����ɑO�����ė\�Ă����K�v������܂��D�Ƃ��낪�C1�̍��Z�ɂ́C�l�X�Ȓ��w�Z���琶�k������̂ŁC�ǂ�ȋ��ȏ����g���Ă����̂��́C�킩��܂���D���̂悤�Ȃ킯�ŁC���w����
3>x��
x<3�Ɠ������Ƃ������Ƃ��K���Ă���̂́CA�Ƃ������ȏ����g���Ă���ꍇ�����ŁC����B,C,D,E�̋��ȏ����g���Ă���ꍇ�ɂ́C�K���Ă��Ȃ��Ƃ������Ƃ́C���Z�̐搶�ɂ͒m�炳��Ă��炸�u�閧�v�ɂȂ��Ă��܂��D�������C���Z�̐搶�́C����ȓ��R�̂��Ƃ��炢�����邾�낤�Ƃ������ƂŁC���Ƃ�i�߂܂��D������C���̊Ԃɂ����Ƃ�������Ȃ��Ȃ邱�Ƃ�����܂��D
�@���Ȃ��̎�����āC���������
7+2x<5x−6������ꂪ�ŏ��̖��@
13<3x����ڍ��͏K���A
3x>13����K��Ȃ��B
x>13/3���������Ȃ��C
������́C���̂悤�ɕό`�ł��܂����C���߂ɇA�ɐi�ނƁC�D�E�ɂ͍s���Ȃ����k������
7+2x<5x−6������ꂪ�ŏ��̖��@
−3x<−13����ڍ��͏K���D
3x>13������̐��Ŋ���ƕs�����̌������ς��E
�A�}�]���ł��w���ł��܂����C�]�����[�̏o�i���H�C1��3000�~�ȏ�Ƃ����ꍇ�॥��D����3�w�N�̌v15��������ے��̉����̂��тɓ��肷��̂́C�����Ȕ������ɂȂ�D
�����A�����̖��́A�p�b�ƌ��̈�ۂƈႤ�����ɂȂ�Ƃ��낪�A���������ɂȂ�܂����B���肪�Ƃ��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���̃O���t�i���萔�������̏ꍇ�j�ɂ��ā^22.11.16
������������Ăق����B
�����m��ҁn�F�A�����肪�Ƃ��D�X����ؕЂ̒l�������̏ꍇ�̖��������Ăق����Ƃ����Ӗ��ł����H
���m�ʂ̕ł���̎���ɑ���n[�������̉������ɂ��ā^22.11.16
�ƂĂ��w�͂����܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����̐����ɂ��ā^22.11.15
���₵�Ă�����e�ƁA�S�R�Ⴄ🖕💢😡㈇
�����m��ҁn�F�ǂ̖��̘b�Ȃ̂��D�N���������₵�Ă���̂��D�������ƈႤ�̂��D�S���ʂ��Ȃ��D�킩��悤�ɏ����܂��傤
���m�ʂ̕ł���̎���ɑ���n[���s���Ɗp�ɂ��ā^22.11.15
���ɗ����܂��� �L��������܂���
�����m��ҁn�F�A�����肪�Ƃ��D
���m��錧/?/?����n22.11.14
���Ȏ��ł��������Ƃ��ł��܂����B���ӂł��A������i�K���͂������Č��Ă͂ǂ��ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��D����y�[�W���鋳�ނ̂����̂ǂ̃y�[�W�̘b�Ȃ̂��������Ȃ��ƁC���̘b�Ȃ̂��ʂ��܂���D�s���{���ȊO�͍Z��,���O�i�y���l�[���j�������Ȃ��D
���m�ʂ̕ł���̎���ɑ���n[���s���Ɗp1�ɂ��ā^22.11.14
�ƂĂ��킩��₷���A�l�ɋ�������ł����I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����`�̕������ɂ��ā^22.11.14
�킩��₷�������ł�
���肪�Ƃ��������܂���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�s�����̉������ɂ��ā^22.11.09
���̖��͉���������Ȃ��Ɖ�������邱�Ƃ��ł��Ȃ����߉��P���Ăق���
�����m��ҁn�F�A�����肪�Ƃ��D���߂������������C�������͉������I�Ɍ�������C���ɂȂ�Ȃ��ƍl����l�̕��������̂ŁC�����͒f��܂�
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝(�������)�ɂ��ā^22.11.09
�ƂĂ��������낢���ł����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�O�p�`�̖ʐ��ɂ��ā^22.11.07
�ǂ����́A�Z���̖ʐςׂ�ƁA�����ƕ�����B
�����m��ҁn�F�A�����肪�Ƃ��D�茘���Z���Ō��Z���悤
���m�ʂ̕ł���̎���ɑ���n[�}�`�P�ɂ��ā^22.11.07
������������₷��
�ł��Ȃ����������ēǂދC������😓😓
�����m��ҁn�F�A�����肪�Ƃ��D�܂��������Ȃ��ق����C�ǂނ̂͊y���ȁD�������C�p��̉���̃y�[�W���C�p����g�킸�ɏ�������C�E�\�ɂȂ�
���m�ʂ̕ł���̎���ɑ���n[�A���������̍���������͑��ɂ��ā^22.11.07
�ƂĂ�������₷�������ł��I���J�ȉ���̌�ɂ܂����̂����������Ă���Ċ��ӂł��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����v�Z�̓�������ɂ��ā^22.11.05
���K�ɂ͂ƂĂ��悩�����ł�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����}�`�C���s���Ɣ��ɂ��ā^22.11.04
���������܂�킩��ł�
�����m��ҁn�F�A�����肪�Ƃ��D�������ɂ���ẮC�ォ��ڐ��̎����b�̓������@�ɂ��̂ŁC�ł��Ȃ��l���ǂނƁC�ǂ����������Ȃ��\������D1�������ǂ�ŁC1��������ɁC�����ϊ��̎��Ԃ��ɂ���ŁC�Ђ炪�ȂŊ��z��������?���̂��߂�?
���m�ʂ̕ł���̎���ɑ���n[�i���Δ�j�A���������ɂ��ā^22.10.30
��ԏo�₷�����Z�������������ƍ���Ă���܂��H
�����m��ҁn�F�A�����肪�Ƃ��D���j���[�����ǂ��āC
���̃y�[�W�Ȃ�
��̂悭�킩������ł����ǂ����ƃo���G�[�V�����𑝂₵�Ă���܂�������Ώ�����܂����肢���܂�🥺🤲�I
�����m��ҁn�F�A�����肪�Ƃ��D??���j���[�������Ă���̂�����C���̎��̃y�[�W�ɐi�߂悢�̂ł͂Ȃ���
���m�ʂ̕ł���̎���ɑ���n[�ω��̊����ɂ��ā^22.10.25
�ƂĂ�������₷�����A�g���₷���ł��B�@���肪�Ƃ��������܂�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������ɒ������K�i���w�����j�ɂ��ā^22.10.24
0.00015
�����m��ҁn�F���₪����̂Ȃ�C���₪������悤�ɏ����܂��傤�D�ԈႢ�̎w�E�Ȃ�C�����ǂ��ԈႢ�Ȃ̂������܂��傤�D�Ȃ��C�h��̓����������邱�Ƃ͂��Ă��܂���D
���m�ʂ̕ł���̎���ɑ���n[�������ɒ������K�ɂ��ā^22.10.17
0.5859375���ɂ��Ă��������B
�����m��ҁn�F�A�����肪�Ƃ��D�h��̓����������邱�Ƃ͂��Ă��܂���D����ɁC�q�˂��Ă��Ȃ����ɓ����Ă݂܂��F0.02304���ɒ����ɂ́C���߂ɕ����100000�ɂ��āC�����������̌`�̕����ɂ���D�ł�����艽�x������D

����ƕ��q��f������������i���w3�N�ŏK���Ă���j

�S�R���Ȃ��ƂĂ��ǂ��ł��I
�O���t�Ȃǐ}���g���Ă��Ă킩��₷�������ł��B
�ł��������������M���E�M���E�ɂȂ��Ă��܂��Ă��Č��鑤���킩��ɂ����Ȃ��Ă��܂������m��܂���B�Ȃ̂ł������������K���ł��I
�����m��ҁn�F�A�����肪�Ƃ��DChromebook�ȂLjقȂ���ł́C�쐬�����s�ԂƈقȂ�s�Ԃŕ\������Ă��邱�Ƃ�����܂��DCtrl+(+)�Ŋg�傷��ƌ��₷���Ȃ�ꍇ������܂��D
���m�ʂ̕ł���̎���ɑ���n[�A���������i���Z�������j�ɂ��ā^22.10.11
���̃T�C�g�̖������Ȃǂ̂��A�ŁA�A�����킩��悤�ɂȂ�܂����I���肪�Ƃ��������܂���‼︎
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Ă�1�ɂ��ā^22.10.07
����������萔�𑽂����Ă����Ƃ�肪���������Əo��Ǝv���܂����B
���̂܂܂ł��ƂĂ������̂ł��������������P���Ă��炦��ƂƂĂ�������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D���̃y�[�W��12��C���̎��̃y�[�W�ɂ����ƈՂ�����肪10��C����ɂ��̎��̃y�[�W�ɂ����Ɠ����肪�����ɂ���܂��D�����Ɓu��萔�𑽂��v�Ƃ́C�������������H
���m�ʂ̕ł���̎���ɑ���n[�����W���̕������ɂ��ā^22.10.03
���߂܂��āB���w�ō��܂������w�̕��������ɗ��p�����Ă�����Ă܂��B���2�̉́u����4��3�̍ŏ����{����6������C���ӂ�12���|���ĕ�����v�̈Ӗ�������A�l���Ă��킩��Ȃ���...�B���̍l�������Ԉ���Ă���̂ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝(�������) �ɂ��ā^22.10.03
�y����������킩��₷����������ł��܂���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�O�����̒藝�̉��p�ɂ��ā^22.09.13
�݊p�̊܂܂��O�p�`�̐������܂߂Ăق����B
�����m��ҁn�F�A�����肪�Ƃ��D���̃y�[�W�̖��2�ɏ����Ă���܂��D
���̃y�[�W��3/4�Ԃ̖��C
���̃y�[�W��5,6,7,8/8�Ԃ̖���
�o��̎d�����w���v�����ɂ킩��₷���ł�
���ɂ͓��ɊW����܂������������Ă�������S�Ă̖��������I������ۂ̃A�j���[�V���������`�x�[�V�����ɂȂ�܂�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�ő���ƍŏ����{���ɂ��ā^22.09.04
�Q�̐��̍ŏ����{���A�ő���̂ǂ��炩�ƁA�����̘a��ς݂̂��킩���Ԃł�2�̐��̋��ߕ��ɂ��ĉ�����Ăق����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D���݁C���w�Z�̋��ȏ��ōŏ����{���A�ő���͎�舵���Ă��Ȃ��悤�ł��D����҂͒��w���łȂ��C�w�K�m�u�t�Ȃǂ��Ƒz�����܂����C���̖��������ɂ́C���Z���wA�ň����Ă��鎟�̌������K�v�ł��D
2�̎��R��A, B�̍ő����G�C�ŏ����{����L�Ƃ����
(1)�@A=A'G, B=B'G�iA', B'�݂͌��ɑf�j
(2)�@AB=GL
���ۂɖ��������ɂ́C�u�̌��v�Ɋւ������A=pαqβrγ����̖̌��́C(α+1)(β+1)(γ+1)����ł���D����ɂ��C�����̉��̂����ŏ����i�Ⴆ��A, B�Ƃ�2���̎��R���j�ɍ�������I��œ����邱�ƂɂȂ�܂��D
���m�ʂ̕ł���̎���ɑ���n[�����}�`�Ɗp�i�������j�ɂ��ā^22.09.03
���ɂƂĂ��𗧂��Ă��܂��I���肪�Ƃ��������܂��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������̉�����===(���������ɂ����@)�ɂ��ā^22.08.31
���������Đ������킩��₷���ĂƂĂ������Ǝv���܂�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�ő���ƍŏ����{���ɂ��ā^22.08.30
�������킩��₷�������ł��B���K�w�K�ɖ𗧂��܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝�ɂ��ā^22.08.30
������₷���}���g���ĉ�����L��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�u�������ɂ����������ɂ��ā^22.08.23
���̉����������J�ɂ܂Ƃ܂��Ă���̂ŁA������₷���ǂ��Ǝv���܂��B�����A�����������ł�����������悤�ɕ\�����Ăق����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�v���O������͒����Ă���͂��ł������C1�ӏ��G���[�������āC�����������̉�����o�Ă��܂���ł������������܂���
���m�ʂ̕ł���̎���ɑ���n[�H�����̔Z�x�ɂ��ā^22.08.22
�������������āA�w�K���Ȃ���ł��`�F�b�N�ł��܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~�ɓ��ڂ���l�p�`�ɂ��ā^22.08.21
�~�ɓ��ڂ���l�p�`�A�ڌ��藝�A���w���w����O��ċv�����ł����ǁE�E�E
�����m��ҁn�F�A�����肪�Ƃ��D�u�~�ɓ��ڂ���l�p�`�A�ڌ��藝�v���u���w���w����O��ċv�����v�Ƃ������Ƃł�����C�����ł͂���܂���---���s�̋��ȏ��Ɍf�ڂ���Ă��܂��D�u�ǎҎ��g���v�u���w���w����O��ċv�����v�Ƃ������Ƃł�����C�O�ɕ��ׂĂ�����u�~�ɓ��ڂ���l�p�`�A�ڌ��藝�v�́C���̖��ɗ����Ă���̂��H
���m�ʂ̕ł���̎���ɑ���n[�s�����̎g�����ɂ��ā^22.08.20
������₷�������}�ł���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������̗��p�ɂ��ā^22.08.19
�������������������͊�ɂȂ�@���̖��������Ă���܂��H
�����m��ҁn�F�A�����肪�Ƃ��DK�Ђ�D�Ђ̋��ȏ��ɂ́C�u�����Ɗ�́w�a�x�͊�ɂȂ�v���Ƃ̏ؖ���肪�o�Ă��܂��D���ɁCD�Ђ̋��ȏ��ɂ́C���̏ؖ��ŁC������
2m,���
2m+1�Ƃ��Đ�������ƁC�悭�Ȃ����Ƃ������Ă���܂��D�����^�����āC�����̓��Ă����悢�D
k, m, n�͐����Ƃ���D
���2k+1�C������2m�Ƃ����ƁC���̍���(2k+1)−(2m)=2(k−m)+1�ƂȂ�D�����ŁCk−m�͐���������k−m=n�Ƃ����ƁC���߂鍷��2n+1�ɂȂ邩��C����Ƃ�����D
�i���l1�jD�Ђ̋��ȏ��ɏK���ē��Ă������C2(k−m)+1�̂܂܂ʼnɂ��Ă��悢�D�Ȃ��Ck−m=n�Ƃ����Ă悢�̂��Ƃ����悤�ȁC�i�����̎q���ɂǂ�Ȗ��O��t����̂��́C�e�̎��R���I�Ƃ����悤�ȁj�b�ɐ[���肵�Ȃ��Ă��\��Ȃ��D
�i���l2�jD�Ђ̋��ȏ��ɏK���ē��Ă������C���2m+1�C������2m�Ƃ����ƁC�����Q�̐��̏ꍇ�����ؖ��ł����C11��2�̍��̂悤�ȏꍇ����ɂȂ邱�Ƃ��ؖ��ł��Ă��Ȃ�����C�_�����ĂɂȂ邱�Ƃ��킩��D
�ƂĂ�������₷���������Ă������肠�肪�Ƃ��������܂��B
�N�C�Y�`���Ŋy�����w�����Ă��������܂����B
���āA���P�_�ł����A�������Â炢�������������Ǝv���܂����B�܂��A�����Z�ƈ����Z�̂����������ė~�����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�����Z�ƈ����Z�̂����Ȃǂ�
���̃y�[�W�ȂǁD�Ȃ��u�������Â炢�������������v�Ƃ����������ł́C�ǂ̉ӏ����ǂ��킩��ɂ����̂�������܂���̂ŁC���P�̖��ɂ͗����܂�����܂łɂ������C�ł����ɗ����Ȃ����P�ӌ��́C�u����̃y�[�W�ŊԈႢ���������悤�ł��v�Ƃ������̂ł����������́C��̓I��Ƃɒu��������C����y�[�W�����鋳�ނ��u�S���������Ă��炨�����I�v�Ƃ����Ӗ��ɂȂ�܂��D�i�����ł͂Ȃ��āCMac���Safari�œǂ݂ɂ���font������Ƃ����b�Ȃ�C�ǂ�font���ǂ݂ɂ����̂��w�E�����ΑΉ��ł��܂����j
�킩��₷�������t�����Ă��Ă��܂��ɍ̓_�܂ł��Ă��炦��̂��ƂĂ�����
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������ƎO�p�`�̖ʐ�2�i�������j�ɂ��ā^22.08.16
�Ȃ��A�����}�`�Ȃ̂��m�肽��
�����m��ҁn�F�A�����肪�Ƃ��D���̎���̎d���̓_���ł��D�ǂ̖��̂ǂ̉�������Ȃ̂��������Ȃ��Ɠ����炦�܂���D�Ȃ��C�p�\�R���p�̍L����ʂ̋��ނ�iPod�Ō��Ă���悤�ł����C�g�їp�̏c���̃y�[�W���ʂɂ���܂�
���m�ʂ̕ł���̎���ɑ���n[�_�Ώ̂Ȑ}�`�ɂ��ā^22.08.11
���̂��������͂Ă����傤�ł����킩��Ȃ��̂ŋ����Ă�������
�����m��ҁn�F�A�����肪�Ƃ��D�M�L�̂̂悤�ȏꍇ�͕ʂƂ��āC�u���b�N�̂ŏ����ꂽ���̂悤�ȃA���t�@�x�b�g�͓_�Ώ̂ƌ�����ł��傤�D�i�m�𖾒��́i�Ђ��t���j�ŏ��������̔����ȑł����݁C�n�l�͖��ɂ��Ȃ����̂Ƃ���jH I N O S X Z����Q�lN N
���m�ʂ̕ł���̎���ɑ���n[�������̕\�����ɂ��ā^22.08.06
�Ȃ����@�ɂ��ď����ł̕\�L�����Ȃ��̂ł����H
1/10��0.1�ǂ���ł��ǂ��Ǝv���̂ł����A
�����ɂ��邱�Ƃ���{�ƂȂ��Ă��鎖�̐������o���Ȃ������̂�
���������������B
�����m��ҁn�F�A�����肪�Ƃ��D���̃y�[�W�̒���18�蒆1�肪�����W���ɂȂ��Ă��܂����CT�ЁCK�ЁCS�ЁCD�ЁCG�Ђ̋��ȏ������Ă��C�e�X30�y�[�W�i���S��j��2�C3�舵���Ă�����x�ł��D
�����Ə����̊W�͏��w�Z�ōς�ł���ƍl���邱�Ƃ������ł��傤�D
�@���悻�̌X���Ƃ��Č����C���w�E���Z�̐��w�́C�����ƕ����ŕ\�����Ƃ������C���Z�Ȍ�Ŏ�������������ł͏����i�ߎ����j���������Ƃ������Ǝv���܂��D
�S��������Ȃ�
�������������Ă��Ȃ���肪�̂��Ă��Ȃ�
�����m��ҁn�F�A�����肪�Ƃ��D�ے肵�߂���ƈӖ����t�ɂȂ�̂Œ��ӂł��D�u�������������Ă��Ȃ���肪�̂��Ă��Ȃ��v�́u����������肾�v
���m�ʂ̕ł���̎���ɑ���n[�����̕ό`�ɂ��ā^22.08.03
���Ȃǂ������āA�����̕�������O�Ƀs�b�^���łƂĂ��悩�����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�s�����̉������ɂ��ā^22.08.03
�f���炵��
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝(�������)�ɂ��ā^22.08.02
��2�̎q���Ɗy���������Ă��܂��B�T���v��������������A���ɍs���܂����ǂ����Ă������Ȃ���������A�ɊȒP�ȕ⏕����������������Ȃ��Ɗ�]���Ă��܂��B��낵�����肢���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D������Ȃ��ꍇ�́C�������Ăł��C�u�̓_�v����ΐ���Ɖ�����o�܂��D�̓_����Ƃ����{�^���������Ȃ���C����Ƃ����{�^���͏o�܂���D
���m�ʂ̕ł���̎���ɑ���n[�A���������i���Z�������j�ɂ��ā^22.08.02
�悭������܂���👏
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����Ǝ��i�}�`�j�ɂ��ā^22.08.01
�O�Ԗڂ̖��̓���������܂���ł����B
���Ȃ炿���Ɠ������Ă�������
�����m��ҁn�F����������Ă���̂ɓǂ�ł��Ȃ��Ƃ������ƂƁC�����ĂȂ��Ƃ������Ƃ́C�����ł͂Ȃ��DMac��Safari�ł��C�R�Ԃ����������o�Ȃ��āC���̖��̓������o��Ƃ������Ƃ͂���܂���D
���m�ʂ̕ł���̎���ɑ���n[�ɂ��ā^22.07.28
�ʉ��ł��������肪�������̂ŕʉ��̉�����ł���ڂ��Ăق���
�����m��ҁn�F�A�����肪�Ƃ��D
���m?��/�v���O���}�[��������n�^22.07.27
�ԐM���肪�Ƃ��������܂��B
txt�ȊO�̌`���̃f�[�^��open�����g�����Ƃ��ł���̂ł��ˁI
�ƂĂ��Q�l�ɂȂ�܂����B
���肪�Ƃ��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m?��/�v���O���}�[��������n�^22.07.26
~mwm48961/programming/python_file1.htm
�������炵�܂��B
�Z�p�̎��Ƃ̔��W�œƎ��̊g���q������Ă��낢��ȃf�[�^�����̊g���q�ɕϊ����邱�ƂŃf�[�^��舵�����y�ɂȂ�̂ł͂Ȃ����Ǝv���A���ӂ�python��txt�ȊO�̃f�[�^����舵�����@�ׂĂ����炱�̃y�[�W�ɂ��ǂ蒅���܂����B
�iword �ꑾ�Y �������Ȃǂ���x�Ǝ��̕����ɕϊ����ĕۑ�����舵�������j
open���̈����ɂ��Ă��܂�n�m���Ă��Ȃ������̂ŁA�ƂĂ��Q�l�ɂȂ�܂����B
�����\�ł�����Atest.txt��ǂݍ��݁Atest.kazu�Ƃ����g���q�ɂ��ď����o���Atest.kazu��ǂݍ��݁Aprint��������������Ă���������Ƃ��肪�����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
�Ⴆ�C���̃v���O�����������悢�ł��傤�D
�@�����t�@�C���́C�Ⴆ��c:\data�̃t�H���_�̒��ɁC�e�L�X�g�G�f�B�^�[terapad�Ȃǂō쐬�ۑ������Ctext.txt�t�@�C���Ƃ��āCYes we can.�Ƃ�������������Ă�����̂Ƃ��܂��D���̃t�@�C�����Ȃ��Ƃ��́C2�s�ڂ���4�s�ڂ܂ł̐擪��#��t���ăR�����g�A�E�g���āC6�s�ڂ�1#���O���āC����������t�@�C���֒��ڏ������߂܂��D
�Ȃ��Cpython����v�����^�[�ŏo�͂���͓̂���̂ŁC8�s�ڂŏ������܂��t�@�C�����Cterapad�ȂǂŊJ���āC��������������ΊȒP�ł��傤�D
�t�@�C�����̊g���q�i.yourname�ƂȂ��Ă���Ƃ���j�́C.exe, .jpg, .pdf, .htm�̂悤�ɃV�X�e�����g������\�肵�Ă�����̈ȊO�Ȃ�@.kazu�ł� .sos�ł� .abc�ł����ł�����ł��D�̂̂悤��8.3���[���i�t�@�C���̎傽�閼�O�p8�����ȓ��ɂ��C�g���q��3�����ȓ��ɂ���j�Ƃ������͂Ȃ��̂ŁC���Ȃ蒷���g���q�ł��\�ł��D
# -----�����t�@�C���̓ǂݏo��------
file1 = open('c:/data/test.txt','r') #2�s��
str1 = file1.read()
file1.close() #4�s��
# -----�����t�@�C���Ȃ��Œ��ڏ������ނƂ�----
# str1 = "Yes we can." #6�s��
# -----�V�K�t�@�C���ւ̏�������----
file2 = open('c:/data/test.yourname','w') #8�s��
file2.write(str1)
file2.close()
���m�ʂ̕ł���̎���ɑ���n[���̒l�ɂ��ā^22.07.19
�ƂĂ�������₷�������������ĕ�����₷�������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������̕\�����ɂ��ā^22.07.19
�搶�̏Љ�Ŏg���Ă��܂����A�������g���₷���Ă����Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�ǂ��搶���I
���m�ʂ̕ł���̎���ɑ���n[���Ώ̂Ȑ}�`�ɂ��ā^22.07.18
�ԈႦ�����́A�o�c��������Ȃ��A���̖��̉������ƁA�����������������ǂ��Ǝv���܂�❗️
�����m��ҁn�F�A�����肪�Ƃ��D�u�q���g�v�Ƃ����{�^���������u���̖��̉������ƁA�����v���\������܂����C���̂��ƂɋC���t���Ȃ��Ƃ������Ƃł����H
���m�ʂ̕ł���̎���ɑ���n[�������̉������ɂ��ā^22.07.18
�y�[�W�̕��ɍ��킹�Ă���������Ɠǂ݂₷���đ�Ϗ�����܂�😰
�����m��ҁn�F�A�����肪�Ƃ��D�u�� �g�єł͕ʕŁv�Ƒ傫�ȕ����Ő擪�ɏ����Ă���܂��̂ŁC�g�єł����Ă��������DiPhone�͌g�тł�→PC�ł�ǂނ̂ɂ͓K���Ă��܂���D
���m�ʂ̕ł���̎���ɑ���n[�A���������̍���������͑��ɂ��ā^22.07.17
�w���v�t���������Ă킩��Ȃ������炻�������Ăǂ�����ĉ������炢�����Ƃ��K�����肷�邱�Ƃ��ł��Ăւ�Ղ��ƂĂ��킩��₷�������Ă��邩��ƂĂ������₷���Ƃ��������l�I�ɗ������₷�������̂ł����Ƃ�����
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�A���������i���Z�������j�ɂ��ā^22.07.16
�����̖��
�����m��ҁn�F�A�����肪�Ƃ��D�����̖��́C���̃y�[�W��E.2�Ƃ������ڂ�C�A��������(����,�����W��)�Ƃ����y�[�W�ɂ���܂���������Ă��邱�Ƃ����₷��̂͂悢���Ƃł͂���܂���D
���m�ʂ̕ł���̎���ɑ���n[�ω��̊����ɂ��ā^22.07.16
y�̑�����=�ω��̊���✕x�̑����ʁH
�����m��ҁn�F�A�����肪�Ƃ��D���̒ʂ�ł�
���m�ʂ̕ł���̎���ɑ���n[���̒l�ɂ��ā^22.07.15
�ƂĂ�������₷���N�C�Y���o�ł�ꂽ�̂ŁC�ƂĂ��y���������ł��B�����āC������ƂĂ�������₷�������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m?��/?����n�^22.07.10
�Ō�t�ł��B�Z�x�v�Z���d���ōs�����Ƃ�����܂����A��l�Ɏ������Ă�ꂸ�w�ђ����ړI�ŗ��p���Ă��܂��B����ł͂Ȃ��ł����A�T�u�X�N�ȂǂōL���������ł���Ə�����܂��B�������������������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�e�ł̌g�єŁi�X�}�z�p�j�͍L�����O���Ă��܂�����������C����y�[�W������̂ŁC�ݒ�ύX����̂��̗͎d���ŁC���ɒ��w���������ނ̕��͎c���Ă���\����ł��D�Ȃ��C�����K���͓��菤����Z�Z�@�̊W�ŁC�Z���C����,�d�b�ԍ���\������`�����ۂ����Ă����悤�ȥ���댯�߂��Đ����ł��Ȃ��Ȃ邨���ꂠ��C�����ł��傤�D
���m�ʂ̕ł���̎���ɑ���n[�A���������̕��͑�2�ɂ��ā^22.07.03
�����e�X�g�̑�ł�点�Ă��������܂����B
�����̖����ڂ��Ă���������ƍK���ł��B
�����m��ҁn�F�A�����肪�Ƃ��D���w�Z�Ō������l�Z�I�Ȃ��̂�
���̃y�[�W�ɂ���܂�
�����Ɩ����o���ė~����
�����m��ҁn�F�A�����肪�Ƃ��D�ڎ���������͂��ł��̂ŁC���̃y�[�W�C����Ɏ��̃y�[�W�Ɛi�߂悢�Ǝv���܂���
���m�ʂ̕ł���̎���ɑ���n[�Q���������̓�������ɂ��ā^22.06.28
���̖��͑S�Čv�Z���ʼn����܂����̂ŁA���͖������Ă����Ɗ������ł�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������̕\�����ɂ��ā^22.06.27
�ƂĂ��ǂ����ɂȂ�܂����B���肪�Ƃ��������܂����B
�y���������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����v�Z�̓�������ɂ��ā^22.06.27
���\�ȒP�Ȗ����肾�����̂ŁA������������lj����Ă���������Ƃ��肪�����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�����v�Z�̓�������10�y�[�W��������ނ̏��߂̃y�[�W���ȒP�Ȃ͓̂��R�̂��Ƃł��D���̃y�[�W�̐擪�ɏ����Ă���T�u���j���[�����āC��̃y�[�W������Ă��������D
���m?��/yaasan����n�^22.06.16
�ؖ��̐i�ߕ�4.3��[ 3/ 5 ]�ɂ��āA���₵�܂��B
https://www.geisya.or.jp/~mwm48961/math3/proof102_3.htm
��ABE=��ADC���ؖ����ꂽ�̂́A�O�p�`�̂R�̍��������̂����A�ǂ̏��������������̂ł��傤���B
���Ă���ǂݎ�邱�Ƃ��ł��܂���ł����B
�܂��A����AD > ����AB �Ȃ̂ŁA�����ɂȂ�Ƃ͎v���Ȃ��̂ł��B
���̃z�[���y�[�W�ŁA���w���w�̕��K������Ă��܂��B
��ς����b�ɂȂ��Ă��܂��B
�����m��ҁn�F�A�����肪�Ƃ��D���̖��͍����Ƃ͊W����܂���D�ؖ��ƌ��������ɈႢ�Ȃ��Ƃ����̂́C���߂����ł��D
�����̊ԈႢ�Ȃǂ��������̂ł�����C��������
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�u�������ɂ����������ɂ��ā^22.06.14
�ǂ�����
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�a�Ɛς̈�������6�ɂ��ā^22.06.14
�P��ԈႦ�Ă��܂����B�Ƃł����Ɨ��K����B
�����m��ҁn�F�A�����肪�Ƃ��D����͎��Ƃ̊��z���H
���m�ʂ̕ł���̎���ɑ���n[�Ϙa�̈�������2�����ɂ��ā^22.06.09
�I�����čs�����͂��₷���ĂƂĂ������Ǝv���܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������ɒ������K�i���w�����j�ɂ��ā^22.06.05
0�C�H�ł͂Ȃ��A�H�C�H�̂������ɒ������@��m�肽���ł��B
�i��j2�C4���H�Ȃ�
�����m��ҁn�F�A�����肪�Ƃ��D���{�̏��w�Z�𑲋Ƃ��܂������C����Ƃ�����āC�t�B���s���C���[�b���b�p�嗤�̏��w�Z�ł����H���{�Ŏg�������̏������ɂȂ��Ă��Ȃ��̂ŁC����̈Ӗ����ʂ��܂��(A) 1,234.56_ (B) 1.234,56_ �̂����̂ǂ�����g���Ă��܂���
���m�ʂ̕ł���̎���ɑ���n[A=B=C�^�̘A���������i�������j �ɂ��ā^22.06.05
A=B=C=D�^�̘A���������͂ǂ̂悤�ɉ����̂ł����H
�����m��ҁn�F�A�����肪�Ƃ��D���w�Z�⍂�Z�����ł́C�����������͏o�܂���D���Ȃ킿�C���w�Z�ł͖��m�����Q�܂ł̘A�����������o����C�������R����悤�Ȗ��́C���ʂȏꍇ�������āu���Ȃ��v�ƂȂ�܂�.���Ȃ��ƂȂ���͒��w�Z�ł͏o���Ȃ��D�܂��C���ʂȏꍇ�Ƃ́C������₷�������C������������2���Ă���悤�Ȗ��ł��D������C���w�Z�ł͏o�肵�܂���D
���m�ʂ̕ł���̎���ɑ���n[���s���Ɛ����̔��ɂ��ā^22.06.01
���������K�^�K�^�������̂Œ����Ăق���
�����m��ҁn�F�A�����肪�Ƃ��DMac���windows�Ƃł́C�t�H���g�̎ߐ��̎�舵�����قȂ�悤�ł��D�������̃R���s���[�^�Łu�A���`�G�C���A�X�v�u�A�s�A�����X�v�u�t�H���g�̊��炩���v�ȂǂɊւ���ݒ��T���āC�uCRT�ɕW���v�Ȃǂ�I������Β��邱�Ƃ�����܂��D
���m�ʂ̕ł���̎���ɑ���n[�������������ɂ��ā^22.05.31
������������Ȃ�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���Ώ̂Ȑ}�`�ɂ��ā^22.05.30
�ƂĂ�������₷���I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�O�p�`�̑��������ɂ��ā^22.05.29
[3]�̖��i��茧2017�N�������j�ɂ��Ď��₪����܂��B
�u�a�d�F�`�b���d�c�F�b�c�ƂȂ邱�Ƃ��ؖ�����v���Ƃ���ސ����āA����͂��Ԃ�A�ӂa�d�ƕӂ`�b�A�ӂd�c�ƕӂb�c���Ή����鑊���ȎO�p�`�Ȃ̂ł͂Ȃ����ƍl���A���a�c�d�Ɓ��`�c�b�������ɂȂ邾�낤�Ɨ\�z���܂����B
���a�c�d�Ɓ��`�c�b�ɂ�����
�ʂb�c�ɑ���~���p������A
�ڂc�a�b���ڂc�`�b
���������ā@�ڂc�a�d���ڂc�`�b�E�E�E�@
�ʂ`�a���ʂ`�b���@�������ʂɑ���~���p�͓���������
�ڂa�b�`���ڂa�c�`���ڂ`�a�b���ڂ`�c�b
������@�ڂa�c�`���ڂ`�c�b�E�E�E�A
�@�A�A���@�Q�g�̊p�����ꂼ�ꓙ��������
���a�c�d�䁢�`�c�b
�����Ȑ}�`�̑Ή�����ӂ̔�́A�S�ē���������
�a�d�F�`�b���d�c�F�b�c
�Ǘ��җl��������������U�@�̉��������Ǝv���܂��B
���̓��ẮA�ؖ����镔������t�߂肵�čl���n�߂����̂Ȃ̂ŁA�ڋ��ȍl������������܂���B
���̂悤�ɉ������琳���Ƃ��ꂸ�A���_����܂����B�i���e�I�ɐ��������Ƃ��O��ł����j
�����m��ҁn�F�A�����肪�Ƃ��D���̓��ẮCO�Ђ̖͔͉Ɠ����ł��̂ŁC�������͂���܂���D
���m�ʂ̕ł���̎���ɑ���n[�O�p�`�̖ʐς̓����ɂ��ā^22.05.26
���X�̉���Łu��PQA�̖ʐς́�ABC�̔����ɂȂ�v�̂Ƃ���́u��PQB�̖ʐς́�ABC�̔����ɂȂ�v�ɂȂ�̂��ȂƎv���܂����B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�P���������̉������ɂ��ā^22.05.26
���w�����ł����A�킩��₷���������Ă��ĂƂĂ�������܂��B
1�A���肢�Ȃ̂ł��������̕\�L����〈���Â炢�ӏ�(���Ƀ}�C�i�X�����̕t��������)������܂��B
������PC���猩�Ă���̂ŁA�X�}�z����݂�ƕ��ʂɕ\������Ă���̂�������܂���B
���̍ۂ͂��߂�Ȃ����B
�����m��ҁn�F�A�����肪�Ƃ��D���݁CFirefox,Edge,IE�̓T�|�[�g���Ă��܂���.Chrome�̂ݓ_�����Ă��܂��D
���m�ʂ̕ł���̎���ɑ���n[�O�����̒藝�̉��p�ɂ��ā^22.05.25
�ȒP������Ǝv��
���p���Ǝv���Ă����̂�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�A���������i���Z�������j�ɂ��ā^22.05.22
�v�Z�@�Ȃǂ����Ă���������ȁ[�Ǝv���܂���.
�����m��ҁn�F�A�����肪�Ƃ��DWindows�Ȃ�u���ׂĕ\���v�u�d��v�ł��傤�D���Z�����ł͎g���Ȃ��ł��傤�D
���m�ʂ̕ł���̎���ɑ���n[�������̕\�����ɂ��ā^22.05.19
�킩��₷�������ł��I���肪�Ƃ��������܂�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�W�J����(x+a)(x+b)�ɂ��ā^22.05.19
�y�����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���Ώ̂Ɠ_�Ώ��ɂ��ā^22.05.17
�ƂĂ�������₷������
�����m��ҁn�F�A�����肪�Ƃ��D
���m���Ɍ��^������]����^22.05.15�n
�v���O���~���O�̖��𑝂₵�Ăق���
�����m��ҁn�F�A�����肪�Ƃ��D������]?--���w�������́C�ǂ��܂ŋ����Ă悢�̂��C�ǂ��܂Ō����Ό����߂��Ȃ̂��ȂǁC���ȏȂȂǂ̃K�C�h���C�����܂��悭�킩��Ȃ�
���m�ʂ̕ł���̎���ɑ���n[�_�Ώ̂Ȑ}�`�ɂ��ā^22.05.10
�����킩��₷���Ă����ł��ˁB���A�y���������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���Ώ̂Ȑ}�`�ɂ��ā^22.05.10
�ƂĂ��ǂ������ł��B����w�K�Ŏg�������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���E�����i�������j�ɂ��ā^22.05.07
�y���R�z(3)�̖�蕶��y�̕ψ悪�|4��x��c�ƂȂ��Ă��܂��Ă���悤�ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�P�����Ƒ������ɂ��ā^22.05.01
�ǂ��Ƃ���E�E�E������₷��
�����Ƃ���E�E�E�Ȃ�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���̒l�ɂ��ā^22.05.01
�����̖�������Ă��炤�ƍK���Ȃ�ł����ǁA�ǂ��ł����H
�����m��ҁn�F�A�����肪�Ƃ��D���̂����l���Ă����܂�
���m�ʂ̕ł���̎���ɑ���n[�����v�Z�i���̒l�j�̓�������ɂ��ā^22.04.30
�����s����̓������ł͍��܂ł̈�����������肭�������`���łƂĖʔ��������ł��B���肪�Ƃ��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�s�����̉������ɂ��ā^22.04.29
�s�����̉�����
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[��@�̌����P�ɂ��ā^22.04.25
���p�ƋC�t���̂��x���Ď����̂��߂�ǂ����������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�S�p�ł����p�ł��ł��܂�
���m�ʂ̕ł���̎���ɑ���n[��@�̌����P�ɂ��ā^22.04.25
���ׂĐ������Ă����̂ł��Ƃ̓}�C�i�X��G�b�N�X�Ȃǂ̂��Y����C���������ł� / �S����ł������A�v�Z���ƂĂ��x���̂ł����Ɨ��K�������ł��B/ �킩��₷������ / �S���ȒP
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������̉��̌����ɂ��ā^22.04.25
�̂��������ǂ��킩��܂���B
�����Ă���������ƍK���ł��B
�����m��ҁn�F�A�����肪�Ƃ��D���܂łɏo��������Ƃ��Ȃ����l�ɁC�����Ȃ�傫�Ȗ��̓�����v������̂́C����Ȃ����łȂ��C�����C������̂��ǂ�������肠��ł��D���Ƃ��C�ʂ肪����̂�������Ɂu���w��������܂���D�ǂ������炢���ł����v�Ɛq�˂Ă��C������`���͂Ȃ��ł��傤�D�u�����߂���v�ƌ���ꂽ�炻�̒����ɏ]���Ƃ����̂����ł��D�u��������܂���v�Ƃ����̂́C��肪�傫�����邩�ǂ����X���X���̊�Ȃ�����ł�.�L���u��������܂���v�ƌ����Ă���̂Ȃ�C���w�Z�����蒼�������Ȃ��͖̂��炩�ł����C���̌����ŏo�Ă��閳�������܂ޕ����̖�������Ȃ��ƌ����Ă���̂Ȃ�C���̕ł��悭�ǂ�ŗ��K���Ă��������D
���m�ʂ̕ł���̎���ɑ���n[�f���������̉��p�ɂ��ā^22.04.25
N����5880�����R���̕����i���j�ƂȂ�悤�ȁA�����Ƃ����������R��N�̒l�����̃A〜�G�̒�����1�I�тȂ����B�Ƃ������̎��͂ǂ�����Ηǂ��̂ł��傤���H
�I�����́@�AN��6 �CN��10 �EN��30 �GN��210�œ������E��N��30�ɂȂ�̂ł������ߕ����킩��܂���
�����m��ҁn�F�A�����肪�Ƃ��D���̕łɏ����Ă�����ɂ��ẮC����ɓ����܂����C�e���̏h��̂悤�Ȗ��̓�����������悤�Ȃ��Ƃ͂��Ă��܂���D����Ă��Ȃ����ɓ�����悤�ɂ��Ă��܂��D15750/N�����R���̕����i���j�ƂȂ�悤�ȁA�����Ƃ����������R��N�̒l�́C2�~32�~53�~7/N���CN=2�~5�~7=70
���m�ʂ̕ł���̎���ɑ���n[�P�����Ƒ������ɂ��ā^22.04.24
�ƂĂ��킩��₷���ł��B0�͒P�����Ȃ̂ł��傤���A�������Ȃ̂ł��傤���B������ڂ��Ă���������ƍK���ł��B
�����m��ҁn�F�A�����肪�Ƃ��D0�͒P�����Ŏ����͌��߂܂���D���Z�ł͈ꌾ�����G��܂����C���w2�N�̒i�K�ŁC�d���̋������悤�ȋc�_�����Ă��g�ɒ����Ȃ��ƍl�����Ă���̂��ǂ����C���w�Z�̋��ȏ��ɂ͏����ĂȂ��悤�ł��D
�y��z 0x=0, 0x2=0, 0x3=0, ...�̂悤�ɁC�P��0�Ə����C�����̌W����0�ł���̂����܂�Ȃ��D
�܂��C�y��z 3=0x+3, 3=0x2+3, 3=0x3+3, ...�ȂǂƏ����邩��C�ǂ�Ȏ��ł��������ł���C�P�����ł����邱�ƂɂȂ�C�p��̈Ӗ������߂��Ȃ��Ȃ�
���m�ʂ̕ł���̎���ɑ���n[�O�p�`�̑��������ɂ��ā^22.04.21
��ώQ�l�ɂ����Ă��������Ă���܂��B
�~���܂ށE�ؖ�����[2]�̉���ł����A�����炭�ȉ��ł͂Ȃ����Ǝv���܂����B
������ɂ���ADE=��ADC=90���c(*1)
����ɂ���ADB=��AEC=90���c(*1)
����ADE�䁢AEC
��ADB�䁢AEC
�܂��A�u(*3')(*4)���Q�g�̊p�����ꂼ�ꓙ��������v
���A�u�Q�g�̕ӂ̔�Ƃ��̊Ԃ̊p�����ꂼ�ꓙ�����v�̊ԈႢ�Ŗ�����A���̗��R�������Ă�����������K���ł�
�����m��ҁn�F�A�����肪�Ƃ��D�������܂����D
���m�ʂ̕ł���̎���ɑ���n[���Ώ̂Ȑ}�ɂ��ā^22.04.21
180�x��]�́B�D�D
�����m��ҁn�F�A�����肪�Ƃ��D�_�Ώ̂Ȑ}�`�����Ă�������
���m�ʂ̕ł���̎���ɑ���n[�������ɒ������K�i���w�����j�ɂ��ā^22.04.18
�ƂĂ�������₷���āA�e�X�g�O�̕��ɖ𗧂��܂����I
���肪�Ƃ��������܂��I
���̍̓_�����Ă����̂ŁA����������܂��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���Ώ�,�_�Ώ́i�܂Ƃ߁j�ɂ��ā^22.04.15
�y�����ł���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�ő���ƍŏ����{���ɂ��ā^22.04.14
�킩��₷��
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�_�Ώ̂Ȑ}�`�ɂ��ā^22.04.12
��肪�������̂ŗǂ������ł��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�_�Ώ̂Ȑ}�`�ɂ��ā^22.04.12
�Ō�̖�茋�\�Y��
�����m��ҁn�F�A�����肪�Ƃ��D�ԈႢ�₷�������W�߂�����ł�
���m�ʂ̕ł���̎���ɑ���n[���̒l�ɂ��ā^22.04.09
�悭����ԈႢ�̂Ƃ���Ɍf�ڂ���Ă���u���̐��̗ݏ�����߂�Ƃ��v�̂Ƃ��뎩�����O����悭�������Ȃ��Ȃ��ĊԈႦ�邱�Ƃ����������̂ł��̕�����₷�������ŗ������邱�Ƃ��ł��܂����I���肪�Ƃ��������܂��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�O�p�`�̓��p�̘a�ɂ��ā^22.04.07
�w���v�{�^���������āA�������₷�������B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����W���C�W���̕�܊W�ɂ��ā^22.04.05
��܊W���Ȃ��ꍇ���L����p���ĕ\���Ă͂��܂��A�ǂ̂悤�ɂ��ĕ\�����Ƃ��ł��܂����H
�����m��ҁn�F�A�����肪�Ƃ��D���Z���w�ŁC��܊W���Ȃ��Ƃ����u�L���v�͎g���܂��C���̉E�ɏ����Ă���I�̐}���u�W���v�ŕ\����A��B=∅
���m�ʂ̕ł���̎���ɑ���n[�������ƎO�p�`�̖ʐ�2�i�������j�ɂ��ā^22.04.03
���X��O, A, P��O, A, B�ɂȂ��Ă���悤�ł�
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[���̂̑̐ρi�������j�ɂ��ā^22.04.02
���6.1�Ɩ��6.2���d���ł�
�����m��ҁn�F�A�����肪�Ƃ��D�����ƂƂ��ƁC�������܂���
���m�ʂ̕ł���̎���ɑ���n[�f���ɂ��ā^22.04.01
�Ō�̕\�͗ǂ��C�Â��ɂȂ�܂����B���肪�Ƃ��������܂��B�ËL�͋��Ȃ̂ł����A�\�����āu6�̔{����+1�Ȃ�����-1�������̂���5,7�Ŋ����Ȃ����̂͑f���v�Ɣ��f����Ηǂ����Ƃ��킩��܂����B
�����m��ҁn�F�A�����肪�Ƃ��D���Ȃ肢�����ɗ��Ă��܂����C���̕\��100�܂ł̐������Ȃ̂ŁC�u�Ⴆ��11�~11=121=6n+1����5�ł�7�ł������Ȃ���11�Ŋ�����D�v�u�Ⴆ�C11�~13=143=6n−1����5�ł�7�ł������Ȃ���11�ł�13�ł�������D�v�Ƃ�����ɁC10�����傫�ȑf���Ŋ����Ȃ����Ƃׂ�K�v������܂��D
���m�ʂ̕ł���̎���ɑ���n[�������^���ɂ��ā^22.03.28
�����ł��܂����B���肪�Ƃ��������܂��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�ω��̊����ɂ��ā^22.03.25
�ω��̊��������߂邽�߂̗��Z �y�[�W��
�Ꭾ���g���������
y=2x+1�ɂ�����x��c����d�܂ő�������Ƃ�
���@�ω��̊�����
(2d+1)-(2c-1)/d-c=2(d-c)/d-c=2
��(2d+1)-(2c+1)/d-c�̌�L�ł���
�����m��ҁn�F�A�����肪�Ƃ��D�_�����Ă��������Ƃ���͂Ȃ��ȁ`�ƕs�v�c�Ɏv���Ă����Ƃ���C�I�I�[�uURL�G�X�P�[�v������%2b�̑����%2d�v�Ə����Ă����̂ŁC−�ɉ����Ă����悤�ł��D�������܂����D
���m�ʂ̕ł���̎���ɑ���n[�O�p�ɂ��ā^22.03.18
�̓_�����ۂɁA�Ԃ����̃C���X�g�Ƌ��ɐ����Ƃ������t�̕\��������Ε�����₷���Ȃ�Ǝv���܂��B���̂Ȃ�A���̓C���X�g�����Ő����Ȃ̂��m�����Ă��A0����͂������̕\���������Ċm�F��������ł��B
���ۂɖ�艉�K�ł���̂́A�ǂ������Ǝv���܂��B�A�j���[�V�����ɂ�������ǂ��Ǝv���܂����B
���͒��w���w�K���Ă�����̂ł��B�T�C�g���^�c���Ă��������A���ӂ��܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�Z�~��lj����܂���
���m�ʂ̕ł���̎���ɑ���n[�A���������i���Z�������j�ɂ��ā^22.03.08
SPI������ɗ��K���܂����B�قƂ�ǖY��Ă����̂ł����A���̃T�C�g����Ԏv���o���₷���A������킩��₷�������ł��B��Ϗ�����܂����I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Q���������̉������i�܂Ƃ߁j�ɂ��ā^22.03.08
x�ix�|8�j��0
�����m��ҁn�F�A�����肪�Ƃ��D���₪����̂Ȃ�C����Ƃ��Đq�˂Ă��������D
���m�ʂ̕ł���̎���ɑ���n[�S�����i�p�[�Z���g�j�ɂ��ā^22.03.04
������👎👎👎👎
���ׂĂ��S�R�o�Ă��Ȃ�����������
�ǂ���
������₷���������Ă��ꂽ��A������₷�������Ă��ꂽ�肵�Ă���鏊���ǂ���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�s�����̉������ɂ��ā^22.03.04
��l�ł����A��������Y��Ă��܂������߁A�ēx�����Ă��܂��B
�s�������Ȃ��ς��̂������ς�̂܂܁A�����������炱����ɂ��ǂ蒅���܂����B
�}�C�i�X�Ŋ���ƕς��̂ł��ˁI�I
���K�����m�[�g�ɂ���Ă��邤���ɗ����ł��Ă��܂����B
�o�b�`�O�[�ł��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�S�����i�p�[�Z���g�j�ɂ��ā^22.03.04
0.00005
�����m��ҁn�F�A�����肪�Ƃ��D���₪����̂Ȃ�C����Ƃ��Đq�˂Ă��������D���̌`�ł́C�ʍs�l�̂�������ɐ���𓊂��Ă���̂Ɠ����ł��D
���m�ʂ̕ł���̎���ɑ���n[���߂��P���s��(1.1)�ɂ��ā^22.03.04
������[�Ƃ������͂������Ă��������Ȃ��Ă��܂��܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�A���������i���Z�������j�ɂ��ā^22.03.02
������₷���I���肪�Ƃ��������܂�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�A���������i���Z�������j�ɂ��ā^22.03.02
������₷���I���肪�Ƃ��������܂�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������C���[�g�ɂ��ā^22.03.01
�̈��ɕ��̕��������܂܂Ȃ��͉̂��̂ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��D����͒��w�Z�̋��ނł��D���w�Z�ɂ͓̈��Ƃ������̂͂���܂���D���Z���Ȃ獂�Z�̋��ނ����Ă��������D
^{\frac{1}{2}}=i)
����������Փx���グ�Ă������Ǝv���܂�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~�ɓ��ڂ���l�p�`�ɂ��ā^22.02.28
�킩��₷���ł�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�m���̋��ߕ��ɂ��ā^22.02.28
�ƂĂ��킩��₷������Œ����Ƃ���͖����Ƃ������܂��B🙅��️
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[��Ԑ}�`�̗p���ɂ��ā^22.02.27
��肪�킩��Ȃ��Ƃ��A�}�Ȃǂŋ����Ă����̂��ƂĂ��ǂ������B
�g���₷���������ƂĂ��ǂ������B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���̂̕\�ʐ��ɂ��ā^22.02.27
�ƂĂ��ǂ������ł�‼️�ȒP�Ȑ����ł��������̂��߂ɂȂ�‼️
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�m��(���Z�������)�ɂ��ā^22.02.25
�y���������ł�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�H�����̔Z�x�ɂ��ā^22.02.21
������ɂ�������
�����m��ҁn�F�A�����肪�Ƃ��D�ǂ����ǂ̂悤�ɂƂ������Ƃ������Ȃ��ƒ����܂���
���m�ʂ̕ł���̎���ɑ���n[�ɂ��ā^22.02.21
���̂������킩��₷���ł��I�I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������ɒ������K�i���w�����j�ɂ��ā^22.02.20
�ƂĂ��킩��₷�����ꂩ����Q�l�ɂ������Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���s���Ɗp�ɂ��ā^22.02.17
�����Ǝv���܂��I
�߂��Ⴍ������ɗ����܂���!
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������ɒ������K�ɂ��ā^22.02.16
���Ɉ����Ƃ���͂���܂���B
�t�ɂ킩��₷�����ł��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�H�����̔Z�x�ɂ��ā^22.02.16
������܂����B���肪�Ƃ��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�m���̋��ߕ��ɂ��ā^22.02.15
�悭�킩��Ȃ���肪�������������̂ŕ��K���Ă��������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�m���̋��ߕ��ɂ��ā^22.02.15
�悭�킩����
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�m���̋��ߕ��ɂ��ā^22.02.15
�I����ł��₷������
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�A���������i���Z�������j�ɂ��ā^22.02.15
�ƂĂ�������₷�������ł�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�ω��̊����ɂ��ā^22.02.14
������܂����I���肪�Ƃ�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝(�������)�ɂ��ā^22.02.13
�ƂĂ����̖��ɗ������B
�����p�Ȃǂ̕\���͓��ꂵ�Ăق����Ǝv�����B
�����m��ҁn�F�A�����肪�Ƃ��D�Ȃ��Ȃ��Y�܂������Ȃ̂ŁC���̃y�[�W�̉��[�ɎQ�l�Ƃ��ď����܂����D
���m�ʂ̕ł���̎���ɑ���n[��Ԑ}�`�̗p���ɂ��ā^22.02.13
�����������������ɓ��Ă͂߂Ȃ�������Ȃ��̂ł������A���������������悤�ɂ��Ăق����ł��B
�}�́A�ƂĂ��������₷�������ł�
�����m��ҁn�F�A�����肪�Ƃ��D�Z�C�Ȑl�����Ɂu�Ƃɂ�����������v�Ƃ����{�^����t���܂����D
���m�ʂ̕ł���̎���ɑ���n[�������ɒ������K�i���w�����j�ɂ��ā^22.02.13
����������ɂ����̂ł��������킩��₷�������炢���Ǝv���܂�
�����m��ҁn�F�A�����肪�Ƃ��D�ǂ����ǂ�������Ȃ��̂�����̓I�ɏ����Ȃ��ƁC�����ǂ��ς�����悢�̂������܂�Ȃ��D
���m�ʂ̕ł���̎���ɑ���n[�ςƘa���l������������ɂ��ā^22.02.12
���w�Z���ł��g������ł��B�Ȃ̂łȂ�ׂ��ȒP��(���w���ł��킩��P��ȂǁA�A�A)���Ă������������ł��B🥺
�����m��ҁn�F�A�����肪�Ƃ��D���ʂ̏��w���Ɉ���������������̂́C�����ł��D
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝(�������) �ɂ��ā^22.02.10
�ȂS�̓I�ɂ킩��Â炢�ł�
�����m��ҁn�F�A�����肪�Ƃ��D������肩��n�߂��番����ɂ����̂ŁC�m���ݒn�n�Ə����Ă��郁�j���[�̊�{��肩�珉�߂�Ƃ悢
���m�ʂ̕ł���̎���ɑ���n[�������ɒ������K�i���w�����j�ɂ��ā^22.02.10
�ƂĂ������Ǝv���܂��i���K���ł��邩��j
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������ɒ������K�i���w�����j�ɂ��ā^22.02.08
0.56
�����m��ҁn�F�A�����肪�Ƃ��D����Ȃ玿��̌`�Őq�˂Ȃ��Ƃ����Ȃ��D�������C�ǂ����̎��̂悤�ɁC�����ł��ׂ����̓���q�˂Ă���Ƃ܂����̂ŁC�Ⴄ��������ē�����D



�ŏ����瓚�������Ă��܂��Ă����̂ŏC�����˂������܂�
�����m��ҁn�F�A�����肪�Ƃ��D�w�͂��߂́C���Ă�������悤�ɂȂ��Ă��܂����C�u����ς���v�{�^���ň���������u���B���v�u�r���o�߂��B���v�{�^�����N���b�N���C�����Ŗ��������Ă��������D���͂Q�肸�U��ނ���C����Ȃ��o�܂��D�x�Ə����Ă����ˁD�{�^�����N���b�N����̂ł��D
���m�ʂ̕ł���̎���ɑ���n[�P�����̕������i���ĕt:���j�ɂ��ā^22.02.08
�悭�킩��Ȃ������̂ŕ��K���Ă��������ł�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�P�����̕������i���ĕt:���j�ɂ��ā^22.02.08
�����ł���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�A���������i���Z�������)�ɂ��ā^22.02.08
�������ǂ��ł��ˁI
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�O�p�`�̖ʐ��ɂ��ā^22.02.07
�ǂ�����
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������ƎO�p�`�̖ʐ��ɂ��ā^22.02.07
�N�C�Y�`���Ȃ̂Ŏ����ōl���ĒP���ɑ��闝����[�߂��A�ƂĂ��֗��ł��肪�����T�C�g���Ɗ����܂����B�ڂ�����������Ă���̂��ƂĂ��悢�ł��B�ǂ��ŊԈႦ���̂��������₷���̂ŕ��������悭�i�݁A��Ϗ�����܂��B�悢���ނ������ĉ�����A���肪�Ƃ��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~�ɓ��ڂ���l�p�`�ɂ��ā^22.02.07
�킩��₷������
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������ɒ������K�ɂ��ā^22.02.04
�������ɒ������������낢�뒲�ׂĂ��āA�ƂĂ��킩��₷�������ƃ��C�A�E�g�������̂ŁA�����Ăق������Ƃ�����A���₳���Ă��������B
���w�Q�N�̋��ȏ��̊m���ŁA�P�̂�������𓊂��ĂP�̖ڂ��o���ׂ�������ʂ̕\������A�\����u�P�̖ڂ��o��m���͂O�D�P�U�V���x�ł���v�Ɠǂݎ��܂��B���̂��Ƃ̕��͂ɁA�u���������ċ��߂��l�����悻�P�^�U�ł��v�Ə����Ă���܂��B�������ɒ������@�͂킩���Ă��͂������ł������A�O�D�P�U�V���P�^�U�ɒ������@���킩��܂���ł����B�ǂ̂悤�ɒ����̂������Ă��������B
�����m��ҁn�F�A�����肪�Ƃ��D

�́u�ł����ł��Ȃ��v�u

�ɓ�������ł��Ȃ��v�̂ŁC����ȏ�ό`����͖̂����ł��D
�@�d����g���āC�P��6�̌v�Z������ƁC0.16666666����ƂȂ��āC�����_�ȉ���R�ʂ܂ł�0.167�ɂȂ�܂��D
�ƂĂ��킩��₷�������ł��B��肪�Ȃ������̂ŁA�������̒蒅�����₷���āA�悩�����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�H�����̔Z�x�ɂ��ā^22.01.31
�ƂĂ�������₷���A�����O�Ɋm�F���邱�Ƃɗ��p�����Ă��������܂����B���P�_�Ƃ��ĂЂƂ�����̂Ȃ�A�����Ƃ����`�ȂǂŁA�܂Ƃ߂Ă��������Ƃ����Ɨǂ��Ȃ�Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D��ԏ��߂ɏ����Ă���܂�
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝(�������)�ɂ��ā^22.01.30
�Q�[�����o�ʼn�����̂ŁA�ǂ�ǂ�͂����܂����B���̖���������ɉߋ���������Ȃ�����������܂����B���肪�Ƃ��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�A���������i���Z�������j�ɂ��ā^22.01.30
�������ł�����悤�ɂ����炢���Ǝv���܂���
�����m��ҁn�F�A�����肪�Ƃ��D�ł�����悢���Ƃ͑�R����܂����C�ł��Ȃ����Ƃ������ł�������ʂP���������Z���^�[���������ʃe�X�g���C�܂��}�[�N�V�[�g�ł���Ă��āC�u���������Ă��̓_�v���邱�Ƃ͂ł��Ă��Ȃ��悤�ł��D
���m�ʂ̕ł���̎���ɑ���n[�s�����̉������ɂ��ā^22.01.30
�ǂ����ĕs�����̌������ς��̂�������Ȃ��ł�
�����m��ҁn�F�A�����肪�Ƃ��D�P���s�����̉������́C����ے��̉����ɔ����āC���݂͍��Z���w�T�ŏK���悤�ɂȂ��Ă��܂��D����20�N�قǂ̊ԂɁC���w�Z���獂�Z�ɂȂ����l�̏ꍇ�́C����ے��̈ڍs���Łu���w�Z�ł����Z�ł��C�K�����o�����Ȃ��v�Ƃ������Ƃ����蓾�܂��̂ŁC���w�Z�̋��ނɂ��⑫�I�ɒlj��������̂ł��D
�@�Ȃ��C���ۂɕ�����悤�ɂ���ɂ́C�����Ɗ�{�I�Ȗ�����̓I�ɉ����Ă݂�����悢�D
���̕��Q��
�P�U�O�l��S�����ɂ���ƁH
�����m��ҁn�F�A�����肪�Ƃ��D��r���鑊�肪���܂�Ȃ���C�䗦�Ƃ��S�����̘b�͂ł��Ȃ��̂ŁC�����������͂��蓾�Ȃ��D���Ȃ��͕��s���ł��D
���m�ʂ̕ł���̎���ɑ���n[�~�ɓ��ڂ���l�p�`�ɂ��ā^22.01.26
���K���̍Ō�̊pd�̑傫�������߂���ŁA���S��ʂ��Ă�����������ɐ܂�Ȃ�������̐����̑g�ݍ��킹�ł���\�����ے�ł��Ȃ��̂ŁA���a�ł���Ƃ��������ݒ肪����Ƃ�蒚�J�Ȃ̂ł͂Ȃ��ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��D�قƂ�ǂ̓������ł���������Ă���C���ۂ��̒ʂ�ł����C�u�����ɐ܂�Ȃ�������̐����̑g�ݍ��킹�ł���\�����ے�ł��Ȃ��v�Ȃǂƌ����o���C���ׂĂ̒����ɂ��āu�����ɐ܂�Ȃ�������̐����̑g�ݍ��킹�ł͂Ȃ��v�Ə������ƂɂȂ�C���ǂ��Ȃ�D
���m�ʂ̕ł���̎���ɑ���n[�O�����̒藝�ɂ��ā^22.01.25
�ƂĂ�������₷�������ł��B�e�X�g�O�Ȃ̂ŏ�����܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝�ɂ��ā^22.01.21
�ׂ��������Ă�������肪����A���̂�������t���łƂĂ��킩��₷�������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[ �ω��̊���(�������) �ɂ��ā^22.01.20
���������ŐV�̂���������������ł�
�����m��ҁn�F�A�����肪�Ƃ��D�V������������������������܂����C�w�K�w���v�̂̂��肪�����āC���w�Z�ŏo������͌����Ă���̂ŁC�Â��Ă��V�����Ă����̌`�͓����ł��D
���m�ʂ̕ł���̎���ɑ���n[�Ă��ɂ��ā^22.01.20
�O���t�B�b�N���悭���Ă�������������₷�����Ăق���
�����m��ҁn�F�A�����肪�Ƃ��D�����v�]�Ȃ̂����H�H
���m�ʂ̕ł���̎���ɑ���n[�������̍����ɂ��ā^22.01.19
����̕������ƂĂ�������₷�������ł������K���鎞�ɊȒP�ɕ��K���o���ėǂ������ł��I
�����m��ҁn�F�A�����肪�Ƃ��D
�m�a�̎R���^�y���M��HOUSE����n�^22.01.18
���͋C�͂ƂĂ��ǂ��ł��B
�e�X�g���Ԓ��ɂ��̃T�C�g���������̂ł����A�ƂĂ��ǂ�
�q���g����b���������Ă���u���`�����������Ƃ��v�ƕ�����̂ʼn���ɐ��w�̃e�X�g��̖{����肱������������ق����ǂ��Ǝv���܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�ڌ��藝�ɂ��ā^22.01.18
�v�_���킩��₷�������Ă����̂͗ǂ����������܂�ɂ��U���ŊȒP�ɋ��߂邱�Ƃ��ł����̂ŗU�������Ȃ����Ă������Ǝv���B
�����m��ҁn�F�A�����肪�Ƃ��DiPad�ł̓e�[�u���i�\�j�̍��ɏ����Ă���T�u���j���[���\������Ȃ��̂ŁC���Ȃ��́C���̃y�[�W�����S�Ҍ����̍ŏ��̃y�[�W���Ƃ������Ƃ��������Ă��Ȃ��悤�ł��D���ڌ��藝1→�ڌ��藝2→�ڌ��藝3→�ڌ��藝4�Ƒ����܂��̂ŁC���ňȍ~�̖�������Ă��������D
���T�u���j���[���\������Ȃ��@��E�u���E�U������悤�ł��̂ŁC�T�u���j���[�̕\���ʒu�������������ł��i����ł���̂łR�����قǂ�����܂��j
���m�ʂ̕ł���̎���ɑ���n[���s���Ɗp�ɂ��ā^22.01.16
��{�I�Ȗ�肩�班��������Ȃ��Ă����`�����ƂĂ��ǂ������ł�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�A���������̕��͑�2�ɂ��ā^22.01.11
�}�t���[��32�p�[�����Ŕ�����2720�~�x�����܂������̒l�i�͂�����ł���
�����m��ҁn�F�A�����肪�Ƃ��D�u��̒l�i�v�u���̒l�i�v�Ƃ͉��̂��Ƃ��ƕ�����Ȃ��܂܂ɁC�P0�����炢�ǂݒ����܂������C�u���̒l�i�v�̂��Ƃ̂悤�ł��D
x�~0.68=2720→x=2720��0.68=4000
���̒l�i��,4000(�~)
�m?���^����n�^22.01.10
�������T���Ă���Ƃ��ɁA���̃z�[���y�[�W�ɂ��ǂ蒅���܂����B�e�X�g�O�ȂǂɂƂĂ��𗧂��܂��B���肪�Ƃ��������܂��B�����������₷���ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����̕ό`�i�������j�ɂ��ā^22.01.10
�ƂĂ����ɂȂ�܂����B�e�X�g�O�ɖ��ɗ����܂��B���肪�Ƃ��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
�m?���^�]�ア����n�^22.01.10
�~�̐����Q�̘A���������̂Ƃ��낪�킩��Ȃ������̂ŁA�������Ă��̃T�C�g�������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D���ԓ������Œʂ���p��͉B��Ƃ��Ă�C���̐l�ɂ͒ʂ��Ȃ��D�~�̐����Q�Ƃ����̂́C���[�N�u�b�N�������̖��O�ŁC�����ɘA���������Ƃ������ڂ�����Ƃ������Ƃł�����C�Ӗ����ʂ��܂��D
���m�ʂ̕ł���̎���ɑ���n[�������ɒ������K�i���w�����j�ɂ��ā^22.01.06
������������₷���A���Ŋm�F�ł���̂�
�ƂĂ��ǂ������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[��`�̖ʐ��ɂ��ā^22.01.06
����Ń|�C���g�ƂȂ镔�������F�ɂ��Č����Ă���邱�ƂłƂĂ��킩��₷�������ł��B�܂����܂œ����ŏo�������ڂ��Ă��������Ă���̂ŌX�����悭�킩��܂����B���肪�Ƃ��������܂�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������.�܂Ƃ��ɂ��ā^22.01.02
����ł͂Ȃ��A���{���狳���Ă�������Ə�����܂�
�����m��ҁn�F�A�����肪�Ƃ��D�ڎ��̍Ō�̃y�[�W����ǂݎn�߂āC�u���{���狳���Ă���v�Ƃ����咣�́C���蓾�Ȃ��D�ڎ��������Ă���̂�����C�O����ǂ�ł�����������ނ����C�~�Ɏ��Ƃɗ��Ȃ��Ȃ������k�����āC�R���̊w�N�������̑O���Ɏ��Ƃɏo�Ă��āC�u�S���킩��Ȃ�����C�ꂩ�狳���Ă���v�Ƃ����đ�\�ꂵ���D����Ȃ��Ƃ��ł���̂Ȃ�C�������Ƃɏo�Ă��鐶�k�́C���ʂȂ��Ƃ����ɗ��Ă���̂��ƌ��킴��Ȃ��H
���m�ʂ̕ł���̎���ɑ���n[�Z�p���Z�q�ɂ��ā^22.01.01
xx1 = 1 * 2 + 3 / 4
document.write(pp1);
�ł͂Ȃ��A
pp1 = 1 * 2 + 3 / 4
document.write(pp1);
�ł͂Ȃ��ł����H
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�}�` �P�ɂ��ā^21.12.30
�����y�����g�킹�Ē����Ă��܂��A���肪�Ƃ��������܂��B
���(�T)�̖���������ł����A
60���̑Β��p�����ʊp
�ł͂Ȃ��ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝�ɂ��ā^21.12.29
��������œ������肪�ʔ����ėǂ������ł��B
����ǁA〜�x�Ɠ�����ƕs�����ɂȂ�̂ł������C�����Ăق����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�p�x�̒P�ʂ́��͊��ɏ����Ă���̂ŁC60�x���ȂǂƏ�������ԈႢ�ł��傤�D
���m�ʂ̕ł���̎���ɑ���n[�����ŕ\���ꂽ���̑召��r�ɂ��ā^21.12.29
�����������Ȃ�ł����A�����K���ĉ�������蒅�ł���Ƃ��낪�ƂĂ��ǂ��ł��I���肪�Ƃ��������܂��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���̕ψ�(�������)�ɂ��ā^21.12.28
���p���Ă��鑤�Ȃ̂ɐ\����Ȃ��̂ł����T�C�g�̈��S��ۏ��Ăق����ł��B
����2�����̕ψ�̖��ł́A��y=�|x2�ɂ��āCx�̕ψ悪�|3��x��a�̂Ƃ��Cy�̕ψ悪�|16��y��b�ł���B���̂Ƃ��Ca, b�̒l�����߂Ȃ����B
�̂悤�Ȗ�肪�����Ƃ���Ɗ������ł��B
�������炵�܂���
�����m��ҁn�F�A�����肪�Ƃ��D�Í����ʐM�̗L���́C�M�ҁi���j�̂悤�ȂP�l�̃G���h���[�U�ʼn����ł�����ƃT�[�o��ݒu���Ă���v���o�C�_�ɂ��������ł��Ȃ����Ƃ��܂܂�Ă���悤�Ɏv���܂��D���̋��ނ̏ꍇ�́CGoogle��Yahoo!�̂悤�Ȍ����G���W�����璼�ڂ���y�[�W�ɗ���ꍇ�͈Í����Ȃ��i�ی삳��Ă��Ȃ��ʐM�j�ɂȂ�悤�ł����C���j���[�t�@�C�������ǂ��Ă��������ƈÍ����ʐM�ɂȂ�܂��D���ہC���Ȃ��̓��j���[�����ǂ��ĈÍ������ꂽ�ʐM���g���Ă��܂��D→�Í����ʐM�𗘗p����ɂ́C���j���[�����ǂ��Ă��������D
�@�Q�����̕ψ�̖��́C���Z�������̈��p�ƂȂ��Ă��邽�߁C���ۂɏo���ꂽ��肵���o���܂���D�Ȃ��C���쌠�I�ɃO���[�Ȉ����ɂȂ�Ȃ��悤�ɁC�L����ʂ̐V���Ō��J����Ă���������Z�̖��Ɍ��肵�Ă��܂��D
���m�ʂ̕ł���̎���ɑ���n[�A���������̉������i����@�j�ɂ��ā^21.12.27
�킩�肸�炢
�����m��ҁn�F�A�����肪�Ƃ��D��Ď��ƕ����̋���ł́C��܂������ށi���ȏ��̂���y�[�W�Ȃǁj���P�N���X�S�����������i���Ƃ��P���ԁj�Ŋw�т܂����C�R���s���[�^��p�������ނł́C�e���ɍ������e���e���̗������₷�������Ŋw�ׂ�i���ɉ����������j�ƌ����Ă��܂��D���e�������ɍ���Ȃ��Ƃ��́C�������ނ�T���悢���ƂɂȂ�܂��D
���m�ʂ̕ł���̎���ɑ���n[�������ɂ��ā^21.12.25
��������������₷���āA�Ԉ�����Ƃ��ɂ́A��������Ă���邩��A�ǂ����ĊԈႦ���̂���������B���ۂɉ������Ƃ��ł��邩���荎���ɂ��q�����āA�������̕��@�̂P�B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������̍����ɂ��ā^21.12.22
������������������A�lj����Ă���������Ɗ������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D���̃T�u���j���[�ɂ��̎��C����ɂ��̎�����̍��ڂ�����܂��DMac��Safari���ƃT�u���j���[���\������܂��H���Windows��Safari�ł͕\������Ă��܂�
���m�ʂ̕ł���̎���ɑ���n[�~�ɓ��ڂ���l�p�`�ɂ��ā^21.12.21
���ʂ����傤�Ǘǂ�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Q���������̓�������ɂ��ā^21.12.21
������������̏o���Ă����Ƃ��ꂵ���ł�
�����m��ҁn�F�A�����肪�Ƃ��D���w�������̖��́C���w�����x���ɂȂ��Ă��܂��D
���m�ʂ̕ł���̎���ɑ���n[1�����ɂ��ā^21.12.21
�ŏ��͂ł��Ȃ��������ǂ��Ƃ���ł���悤�ɂȂ��Ă悩����
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~�ɓ��ڂ���l�p�`�ɂ��ā^21.12.20
�ȒP�Ȗ����ڂ����Ă��Ĕ��ɂ킩��₷�������ł��I�Ŏv���o���Ă��鎞�ɕs���ɂȂ��Ċm�F�����������̂łƂĂ�������܂����I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�s�����̉������ɂ��ā^21.12.16
�A���s�����̕��@���ꏏ�ɏ����Ă���������Ɗ������ł�
�����m��ҁn�F�A�����肪�Ƃ��D���̃T�u���j���[�ŘA���s������I��ł��������D
���m�ʂ̕ł���̎���ɑ���n[�A���������i���Z�������j�ɂ��ā^21.12.15
�ƂĂ��ǂ�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�ڌ��藝�ɂ��ā^21.12.15
�������o��悤�ɂ��Ă�������
�����m��ҁn�F�A�����肪�Ƃ��DHELP�L�[�������C����E���o�܂��D
���m�ʂ̕ł���̎���ɑ���n[�����`�̕������ɂ��ā^21.12.14
�@���ɕ��ɂȂ�܂����B
�A�}���ɗ���͂����܂�܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Q�_�Ԃ̋����̌����ɂ��ā^21.12.13
�����Ǝv���܂�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�m��(���Z�������)�ɂ��ā^21.12.09
���w���ł����A���w�ɂ��m���͏ꍇ�̂����Ƃ��ďo�Ă���ƕ����ċ����������܂����I��������������ėǂ������ł��I���̉�����킩��₷�������ł��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~�ɓ��ڂ���l�p�`�ɂ��ā^21.12.08
�킩��₷�������B���ƁA�ÎZ�ł��Ƃ���ŏ��̊�b�̖����肾�����̂ŁA�S������邱�Ƃ��ł����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~�ɓ��ڂ���l�p�`�ɂ��ā^21.12.08
�����̗p�����̕��ŁA�~�ɓ��ڂ���l�p�`�������炸�T���Ă��܂����B
���ɕ�����₷�����ɂȂ�܂����I���肪�Ƃ��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������ƎO�p�`�̖ʐ��ɂ��ā^21.12.07
�ƂĂ��킩��₷���I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������̕\�����ɂ��ā^21.12.07
�͂��߂܂��Ė��W�̖��̓����Ł�6=⁻R²+5�Ɖ����̂ł��A�r�����͓����ł�����
��6=5-R²�ƂȂ��Ă�܂����B�ǂ���ł��ǂ��̂��A�̂悤�ɒ����������ǂ��̂����킩��܂���B�܂����̗��R����������Ē��������Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D���ɏ������w�肳��Ă��Ȃ�����−x+1��1−x�ɓ������̂ŁC�ǂ���ł��悢
���m�ʂ̕ł���̎���ɑ���n[�ꎟ���ɂ��ā^21.12.07
������lj��x�����킵����ł����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�ꎟ���ɂ��ā^21.12.07
�s�������|�C���g�t�ŁA���������āA���̉��̕��Əd�Ȃ�Ə����ǂ݂Â炢�ł��B�ł�����������Ă킩��₷���ȂƎv���܂����B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�ꎟ���ɂ��ā^21.12.07
����̈ꕔ�����̕����Əd�Ȃ��Ă���Ƃ��낪����̂ŁA���P���Ăق����ł�
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�ꎟ���ɂ��ā^21.12.07
����������������Â炩�����ł�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Q�_��ʂ钼���̕������ɂ��ā^21.12.06
��������ɂ��̂�����܂������@�ʔ��������ł�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[1���ϊ��ɂ��ā^21.12.06
�����̊Ԋu���L���Ă��������B
�����m��ҁn�F�A�����肪�Ƃ��D���Ԃ�s�Ԃɂ��ẮC���ʂȐݒ�͂��Ă��܂���D�����C�g�債�ēǂ݂����Ƃ������Ƃł�����CFirefox�ł��uCtrl+�v�łł���͂��ł��D���x�����Ή��x���g�傳���.���ɖ߂��ɂ́uCtrl-�v
���m�ʂ̕ł���̎���ɑ���n[���̂̕\�ʐ��ɂ��ā^21.12.05
�����K���ĂȂ�
�����m��ҁn�F�A�����肪�Ƃ��D�u�����K���ĂȂ��v�Ƃ������Ƃł����C���w�P�N���̐��w�̋��ȏ��ɂ́C���ׂĉ~�̖ʐς̌����������Ă���C���̓����y�[�W�����̋ߎ��l��������Ă��܂��D
���m�ʂ̕ł���̎���ɑ���n[�������ɒ������K�ɂ��ā^21.12.04
�����u�Ԃɂ������悭���������̂ŗǂ������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�ω��̊����ɂ��ā^21.11.30
�Ō�̖�肪���Ԃ��Ȃ��ĉ������Ƃ��ł��Ȃ������B������X���X��������悤�ɂ��܂�
�����m��ҁn�F�A�����肪�Ƃ��D�u���Ԃ��Ȃ��āv�Ƃ́C���ƒ��ɂ�����Ƃ������Ƃ���
���m�ʂ̕ł���̎���ɑ���n[�ω��̊����ɂ��ā^21.11.30
�ω��̊��������߂�̂��Ax�̊����o�������������̂ŊȒP�ł����B
�����m��ҁn�F�A�����肪�Ƃ��D�ux�̌W���v�̂��Ƃł����H
���m�ʂ̕ł���̎���ɑ���n[�����}�`��������ɂ��ā^21.11.29
�i�����}�`�������j�̖��P�ɂ��Ď��₪����܂��B
���́A���̂悤�ɉ����܂����B
�_�l�C�m��ʂ�A�ӂ`�a�ɕ��s�Ȑ����Ђ��B
���m�l�b�Ɓ��`�a�b��
���ʂȊp�Ȃ̂Ł@�ڂm�b�l���ڂ`�b�a
�`�a//�m�l���@���s���̓��ʊp�͓������̂Ł@�ڂm�l�b���ڂ`�a�b
�Q�g�̊p�����ꂼ�ꓙ�����̂Ł@���m�l�b�䁢�`�a�b
�����Ȑ}�`�́A�Ή�����ӂ̒����̔�͂��ׂē���������
�m�b�F�`�b���m�l�F�`�a���P�F�Q
���m�l�o�䁢�a�`�o���
�o�l�F�`�o���m�l�F�`�a���P�F�Q
����āA�`�o�F�o�l���Q�F�P
���͐����������̂ł����A�Ǘ��l�l�̉�@�Ƃ͈Ⴂ�܂��B
�܂��A�a�l�F�l�b���P�F�P�̏������g�킸�ɓ����o���܂����B
���Œ��������͖����������߂ɕK�v�ȏ����ł���A�s�K�v�ȏ��������͂����Ȃ��A
�܂��A�f�ڂ���Ă����@�����Ȍ��ȕ��@������Ȃ�A���̉�@���f�ڂ���͂��Ȃ̂ŁA���̉������́A�ǂ����Ԉ���Ă���̂ł͂Ȃ����A�ƍl���āA��������肢���܂����B
��낵�����肢�������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D��ԏ��߂̉��肪�Ԉ���Ă��܂��D�u�_�l�C�m��ʂ�A�ӂ`�a�ɕ��s�Ȑ����Ђ��B�v�ȂǂƂ������Ƃ͂���܂���D�u�a�l�F�l�b���P�F�P�̏����v����������Ă���ꍇ�Ɍ���uMN//AB�v�ɂȂ�܂��D
•�u�s�K�v�ȏ��������͂����Ȃ��v�Ƃ������Ƃ͂���܂���D��w�������Ȃǂł��C�i���̃��x���̉����āH�j���d�ɁE�璷�ɏ������������ꍇ�́C������ł�����܂��D
• �u�f�ڂ���Ă����@�����Ȍ��ȕ��@������Ȃ�A���̉�@���f�ڂ���͂��v�Ƃ������Ƃ͌���܂���D���̉�@����u�҂ɕ�����Ղ����ǂ������d�v�ł��D
���m�ʂ̕ł���̎���ɑ���n[�w���@���ɂ��ā^21.11.29
���肪�Ƃ��������܂��B
�����悭�Z�܂��Ă��ĕ�����Ȃ��Ƃ����������܂����I
�����Č����ΐF�̍\�������₷�����ė~�����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D���₷���F�Ƃ͉����H�Ȃ��Ȃ�������ł�--�ΏƐ������������ʂ��₷������ɃM���M�����Ĕ��₷���Ȃ�C�Ώ̐����������ʂ��ɂ����Ȃ�D���̑��C�F�n���̐F�͗����I�ɂȂ�邪�C�ǎ҂���̉������Ɍ��Ă���̂��ɂ���āC�F�n���͔������悤���悢�i����ɂ����Ȃ邩��j�Ƃ����c�_������܂��D
���m�ʂ̕ł���̎���ɑ���n[�A���������̍����ɂ��ā^21.11.29
�����1��
��P�̉��i���݂���Q�̉��i����50�~�����C�݂���R�̉��i����30�~�������̂Ƃ���D
�݂���P�̉��i�� x �i�~�j�C��P�̉��i�� y �i�~�j�Ƃ���ƁC x , y ���������A����������
��P�̉��i�����Ă������� ���肢���܂�
�����m��ҁn�F�A�����肪�Ƃ��D���̃y�[�W�́u�������̍����v�̃y�[�W�ł��D�������̉�������
�u�������̉������v�̃y�[�W�ɏ����Ă���܂��D
���߂Ɋ�b�I�Ȃ��Ƃ�������Ă����̂ŁA���p�Ŏg���₷���A�킩��₷���ĂƂĂ������Ǝv���܂����I�܂��A�����ǂ�������ŗǂ������Ǝv���܂��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����_�E�O���_�̐}���ɂ��ā^21.11.24
�ƂĂ�������₷���ėǂ������ł��I�ƂĂ�������܂���❗
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����i�S����,����,�����j�ɂ��ā^21.11.20
�����Ղ������珙�X�ɓ�Փx�t����W�J���ė���x�����߂鏇���ɕ����쐬����Ă���̂Ŗ�肪�����Ȃ������Ƃ��A������x���_�ɖ߂��荀�ڂQ��S�����Ă��܂��B��ϑf���炵�����ނ��A���ӂ̔O�Ɋ����܂���L�������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�P�����̃O���t�̏������ɂ��ā^21.11.19
�������킩��₷�������ł��B���肪�Ƃ��������܂�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝(�������) �ɂ��ā^21.11.18
�⏕�������������̂ł�����悤�ɂ��Ă��������B���肢���܂�!
�����m��ҁn�F�A�����肪�Ƃ��D���ʂ̃p�\�R���Ȃ�y�C���g�͕t���Ă��܂��D�܂��C������@��ǂ܂Ȃ��Ă��C�P���Ɍv�Z�p�����g���Ώ��w���ł����͕`���܂�
���m�ʂ̕ł���̎���ɑ���n[�s�����̉������ɂ��ā^21.11.17
(3)�ɂ��ĉ����-5�Ə����Ă���܂���-4�Ƃ̊ԈႢ�ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝�ɂ��ā^21.11.16
�킩��₷���ĂƂĂ��ǂ������Ǝv���܂�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Ă��ɂ��ā^21.11.16
�摜���r���̂��Y��ɂ��ė~�����ł�
�ǂ�����ĉ���̂���������ɂ��������̂ŁA�̎d�����L�ڂ��ė~�����ł�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�O�p�`�̓��p�̘a�ɂ��ā^21.11.15
���ɗǖ�Ŗ����Ƃ͎v���Ȃ�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���W�ɂ��ā^21.11.15
�����Ɩ�萔�𑝂₵�Ăق����B
�����m��ҁn�F�A�����肪�Ƃ��D��萔�́C���̃y�[�W�C���̎��̃y�[�W�i�߂Α����܂��D
���m�ʂ̕ł���̎���ɑ���n[���W���_1�ɂ��ā^21.11.15
��萔�����Ȃ��Ɗ������B
�F�����������킩��₷���F�ɂ���ƂȂ��悢�Ǝv���܂����B
�����m��ҁn�F�A�����肪�Ƃ�.��萔�́C���̃y�[�W�C���̎��̃y�[�W�i�߂Α����܂��D
���m�ʂ̕ł���̎���ɑ���n[���s���Ɗp�ɂ��ā^21.11.14
�����𗧂��܂������肪�Ƃ��������܂�😭😭😭
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~�ɓ��ڂ���l�p�`�ɂ��ā^21.11.13
����Ɛ}�`���������₷�����Ȃ��Ă��ď�����܂����I�I���肪�Ƃ��������܂��I�I�I�I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�H�����̔Z�x�ɂ��ā^21.11.13
�{���ɂ悭������܂����I�I���肪�Ƃ��������܂�😭
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�ꎟ�������i�������ƌ��Z�̎d���j�ɂ��ā^21.11.12
���̖���m��ׂ����R�́A�ꎟ���������킩��Ȃ���������ł��B�ł��A���������ׂāA�����Ȃ��Ƃ��Ƃ���悤�ɂȂ�܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Q�_��ʂ钼���̕������ɂ��ā^21.11.12
�F���g���Ă��āA�ƂĂ��킩��₷�������ł��B
�̓_���Ă����̂̓h�L�h�L���Ċy�����ł��B
�Q�T�Ԍ�Ɋ����e�X�g���T���Ă��܂��B
�O��̃e�X�g�ł́A���w�����ψȉ��ł����B����Ȍ����ς���ׂ��������ƂŏK�������̕��K�����Ă��܂��B
�����Ă��܂��܂��̃T�C�g�ɏo��܂����B
�������l�ō��܂łɏK�������Ƃ̗v�_��}���鎖���ł��Ă��܂��B
���w���o����y���������߂Ċ����Ă��܂��B
���̒��q�Ő��w�ɗ����������čs���܂�‼️
�ڎw���P�O�O�_‼️
�����m��ҁn�F�A�����肪�Ƃ��D
��?���m�H����^21.11.08�n
�Ǘ��l�l�B�����ł���ˁB���炢�����܂����B���w���w�@2�N�@�m���@���Z�������@�K������������1 �ł��B��낵�����肢�������܂�
�����m��ҁn�F�A�����肪�Ƃ��D�u�����������₷���̂ŏ�����܂��B�v������u������L�q���Ē�����v�Ƃ������Ƃ͂Ȃ��ł��D�Q,�R���Ă݂�ΐ����ɓ�����܂��D
��?���m�H����^21.11.07�n
�����������₷���̂ŏ�����܂��B�K�����̖��ł��A�����Ɖ�����L�q���Ē�������肪�����ł��B��낵�����肢�������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D���牽�S�y�[�W�̋��ނ�20�N�قǂ����č�����Ƃ��Ɂu�K�����̖��v�ƌ����Ă��C�ǂ̃y�[�W�̉��̘b�����Ă���̂��ʂ��܂���D
���m�ʂ̕ł���̎���ɑ���n[�H�����̔Z�x�ɂ��ā^21.11.06
�H�����̖�肪��R�����Ċ������ł��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���s���Ɗp�ɂ��ā^21.11.04
������쓮���܂���ł����A���̐F�������Z�������猩���₷���Ǝv���܂�
�����m��ҁn�F�A�����肪�Ƃ��D���̔Z���ƍ쓮�͊W����܂���DiPad�Ō����ɂ����ƌ����Ă�����悤�ł����CiPhone, Android, Windows�ł͖��Ȃ��쓮���܂��D�֎�̂悤�ȋ���Ȏw��Ń^�b�v����Ƃ��̓Y�[���C�����Ă����Ƃ���������悢�ł��傤�D
���m�ʂ̕ł���̎���ɑ���n[�ω��̊����ɂ��ā^21.11.02
�ƂĂ�������₷���ł��B���肪�Ƃ��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����̐����ɂ��ā^21.10.31
�����̐�����d����0�ł͂Ȃ�������Ȃ��ł����H
�����m��ҁn�F�A�����肪�Ƃ��D���̘b�����Ă���̂����ʂ���܂łɂR��������܂����D�������̎��Ƃ̂������̋��ȏ��ɏ����Ă���b���C�������̃y�[�W�Ɏ��₵�āC�ς�����l���ȂƎv���Ă��܂���������C����ƕ�����܂����D����(D)��C�͂O�ł͂Ȃ����ł���������ł�
���m�ʂ̕ł���̎���ɑ���n[�P�����̕��͑��ɂ��ā^21.10.22
�ψ�Ȃǂ��A�����Ăق����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�ψ��ω��̊����́C��ɒ��w�R�N���ŏK���܂��D���w�R�N�̖ڎ�����T���Ă��������D
���m�ʂ̕ł���̎���ɑ���n[�l���v�Z�̗D�揇���ɂ��ā^21.10.19
�ݏ�Ə��@�͂ǂ�����ŏ��Ɍv�Z����Ηǂ��ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D�u(I)��(II)��(III)��(IV)�̏��ɍs���܂��v�Ə����Ă���̂ŁC(II)�̗ݏ��(III)�̐ρE�������D��ł��D
�@�������C���̋^�₪�����ɖ��ɂȂ��ʂ͍l���ɂ����ł��D
•

�������Ƃł����C

•

�������Ƃł����C

• ����ɑ��āC���̕ό`��(I)�̋K���ł��D
^2=\frac{16}{9})
�Ō�̗�肪�ƂĂ����ɗ������B
�����O�ɗ��p�����Ă��炢�܂����I�I
�i�w�Z�ł����S�R���ɗ����܂���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���s���Ɗp�ɂ��ā^21.10.18
�ȒP�������B���p��肪�ق���
�����m��ҁn�F�A�����肪�Ƃ��D�ڎ��łQ���ɓ�����肪����܂��D
���m�ʂ̕ł���̎���ɑ���n[2�����̃O���t�ƌW���̕����ɂ��ā^21.10.17
���x�����e�X�g�Ŗ{���ɏ�����܂����B������₷���ėǂ������ł��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�s�����̉������ɂ��ā^21.10.16
�ƂĂ��������ł������K�ɂȂ�܂����B
������������������Ă��������ȂƎv���܂����B
�����m��ҁn�F�A�����肪�Ƃ��D�P���s�����̉������́C�����ԁi�P�O�N�ȏ�j���w�Z�ŏK��Ȃ����ƂɂȂ��Ă��܂������C���Z�ł�������苳���Ă��鎞�Ԃ��Ȃ����Ƃ�����܂����D���̋߂邽�߂ɋ��ނɂ������̂ŁC���ՂȖ��ɂ��Ă��܂�������݁i�ߘa�j�ł́C���w�Z�̋��ȏ��ɂ������Ă���܂��D
���m�ʂ̕ł���̎���ɑ���n[�������̍����ɂ��ā^21.10.14
������������₷���Ă悩����
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝�ɂ��ā^21.10.13
�ƂĂ������Ǝv���܂�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�A���������i���Z�������j�ɂ��ā^21.10.13
�������킩��₷�������ł�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����̕ό`�ɂ��ā^21.10.11
6x�[2y�[4��0�ɂ��Ẳ����������ĉ�����
�����m��ҁn�F�A�����肪�Ƃ��D
�A�j

��
x�ɂ��ĉ���
x�̍������ӂɁC���̍����E�ӂɈڍ�����

���ӂ�
x�̌W���Ŋ���

�C�j

��
y�ɂ��ĉ���
y�̍������ӂɁC���̍����E�ӂɈڍ�����

���ӂ�
y�̌W���Ŋ���

���d�v�F�u6x�[2y�[4��0�ɂ��Ẳ������v�Ƃ������̂͂���܂���D��Ŏ������悤�ɁC�A�j

��
x�ɂ��ĉ����C�C�j

��
y�ɂ��ĉ������Ƃ͂ł��܂��D
���̒l�̗�肪�悩����
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~�ɓ��ڂ���l�p�`�ɂ��ā^21.10.10
��ԍŌ�̖��̉���ŁA���S�̏�ɗ��~���p�Ə��������A���a(180�x)�ɑ���~���p��90�x�̕����킩��₷�����Ǝv���܂�
�����m��ҁn�F�A�����肪�Ƃ��D�m���ɂ��������̂Œ������܂����D�����������܂��Ă���u���a�̏�ɗ��~���p�v�ł��D
���m�ʂ̕ł���̎���ɑ���n[�����Z�̎d�g���ɂ��ā^21.10.08
�����̓_���܂������e�����̉��ɁuNS�v�Ƃ����\������A�܂�Ƃ��됳���Ȃ̂��s�����Ȃ̂�������Ȃ������B
�����m��ҁn�F�A�����肪�Ƃ��DWindows���Chrome��Android���Chrome�ł͐���ɍ쓮���܂����CMac OS X 10���Chrome�ł͐���ɍ쓮���Ȃ��Ƃ������Ƃł��傤���H�����CNA�iNOT A NUMBER�j�Ƃ����G���[���b�Z�[�W�͕��������Ƃ�����܂����C�uNS�v�͕��������Ƃ��Ȃ�
���m�ʂ̕ł���̎���ɑ���n[�O�ӂ̒������^����ꂽ�O�p�`�ɂ��ā^21.10.06
�m������̌������������悤�ȁc?
�����m��ҁn�F�A�����肪�Ƃ��D�y�[�W�̐擪�ɁC�����͂��邪�u���w���łł��Ȃ��Ă����v�ł��v�Ə����Ă���̂ŁC�o����K�v�͂Ȃ��D�o������̂ł͂Ȃ��Ƃ������Ƃł��D
���m�ʂ̕ł���̎���ɑ���n[�P���������̉������ɂ��ā^21.10.05
�e�X�g���̎Q�l�ɂ����đՂ��܂�����
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Q���������̓�������ɂ��ā^21.10.04
��Փx�͒Ⴂ���ł����A���K�Ƃ��Ďg����Ǝv���܂����B
���肪�Ƃ��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D�������̃y�[�W�Ȃ̂ŁC���ۂɏo����肪�����Ă���܂�
���m�ʂ̕ł���̎���ɑ���n[�����̐����ɂ��ā^21.10.04
�����̂��������킩��Ȃ������̂ŁA�킩��₷���āA�����Ǝv���܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m?? / �g�̖������^21.09.28
�ψ��a b�����߂�̂��o���Ă�������
�����m��ҁn�F�A�����肪�Ƃ��D
���̃y�[�W
�}���J�N�J�N���Ă��ĕ�����ɂ����̂ʼn��P���Ă���������Ƃ��ꂵ���ł��B
���̑� ������₷������ŁA�X�ɗ�肪����̂ł��̏�ŗ���x���m�F�ł��ėǂ������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�J�N�J�N�̈Ӗ���������܂��C�S���C�~�ɓ��ڂ���l�p�`�̖�肾����C�l�p�`���p�����Ă���͓̂��R�ł��D
���m�ʂ̕ł���̎���ɑ���n[�ŏ����{���̉��p����ɂ��ā^21.09.22
���肪����
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�A���������̍���������͑��ɂ��ā^21.09.18
�����t���Ă���������Ɗ������ł�
�����m��ҁn�F������Ή�����o�܂��D���Ȃ���Ή���͏o�܂���D������Ȃ��ƌ����Ă���l�́C�P������ɓ����Ă��Ȃ��Ƃ������Ƃ�\���Ă��܂��D
���m�ʂ̕ł���̎���ɑ���n[�Q���������̓�������ɂ��ā^21.09.12
�ł���A���Z����̖����ڂ��Ă���������Ƃ��肪�����ł�
�����m��ҁn�F�A�����肪�Ƃ��D�n����H�u���Z����v�̈Ӗ����s���ł��D
���m�ʂ̕ł���̎���ɑ���n[�P�����Ƒ������ɂ��ā^21.09.11
���w���D���Ȏ��͂��������ɂȂ邵�������ł����A���Ȑl�͐��������������肷��Ƌ��ӎ��������Ȃ��Ă��܂��Ǝv���܂��B�Ȃ̂ŁA�L�����N�^�[����肻�̎q�ɒ��点��A�Ƃ����̂͂������ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������̕\�����ɂ��ā^21.09.11
�������킩��₷���ĂƂĂ��ǂ������ł��I�͂��߂͑S�R�����ł��܂���ł������A���̃T�C�g�����Č���ƁA�������킩��₷���ĂƂĂ��Q�l�ɂȂ�܂��I���肪�Ƃ��������܂����I�B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Q��C�������C���[�g�ɂ��ā^21.09.08
2���[�g10�̓��Ȃǂ̌v�Z�͂ǂ�����Ă���̂ł����H�@�y�킩��ɂ������͂ł��݂܂���B���ԐM����������K���ł��B�z
�����m��ҁn�F�A�����肪�Ƃ��D���j���[�����ɂ��ǂ�C�Q,3���ڌ�ɏo�Ă��܂��D
���m�ʂ̕ł���̎���ɑ���n[�����̕ό`�i�������j�ɂ��ā^21.09.07
������ƂĂ�������₷��������܂���🙇��️
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���l���E�X�̒藝,�`�F�o�̒藝�ɂ��ā^21.09.06
�`�F�o�̒藝�̎O�p�`ABC�̊O���ɓ_O�����鎞�̏Ɩ����ǂ݂����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�Ɩ����ؖ��D�e��������Ă�������
���m�ʂ̕ł���̎���ɑ���n[���ލ��ɂ��ā^21.09.05
���ލ���I�ԂƂ��ɒ萔���͏����H
�����m��ҁn�F�A�����肪�Ƃ��D�萔���̓��ލ��͒萔���ł�
���m�ʂ̕ł���̎���ɑ���n[�ω��̊����ɂ��ā^21.09.01
�Q�l�ɂȂ鏊�����肠�肪���������ł��B���肪�Ƃ��������܂����B�������C�ꕔ���������ł��Ȃ���������������i���ɕ����j�r�������ڂ��������Ă������������ł��B���肢���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�����ɂȂ�ꍇ�ɂ��ڂ���������Ă���܂�
���m�ʂ̕ł���̎���ɑ���n[�������g�������ɂ��ā^21.09.01
���^�b�v�ʼn{���ł���@�\�͂ƂĂ��ǂ��̂ł����A���x���ԈႦ���I�������Ă��܂����ꍇ�͉�����\�������A�Ȃǂ̉���@�\���ق����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�u������Ȃ��Ƃ��͖���I��ł���m����n���N���b�N�v�Ə����Ă����ˁI������\������Ă��Ă��C�܂�������Ȃ��Ƃ������Ƃł����H
���m�ʂ̕ł���̎���ɑ���n[2���������̉��ɂ��ā^21.08.31
�ƂĂ�������₷���ăe�X�g�ɍs���������ł��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[��������(��{) �ɂ��ā^21.08.30
�������킩��₷�����A�o���Ȃ��������������𗝉��ł��Ċ������ł��I���肪�Ƃ��������܂��A�A�I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������̕��͑��ɂ��ā^21.08.30
���1�́i1�j�̒ߋT�Z�̉����250�{��650�~�{�ƌ�A�ɂȂ��Ă���B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂����D
���m�ʂ̕ł���̎���ɑ���n[�ω��̊����ɂ��ā^21.08.29
�ƂĂ�������₷���āA������܂���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�O�p�`�̖ʐς̓����ɂ��ā^21.08.28
���p�̖��Ƃ��Ċ��p�����Ă��������܂����B
�������킩��₷���ƂĂ�������܂���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����̐��ɂ��ā^21.08.27
�}�E�X�𐔒�����̂����ŃN���b�N���邱�Ƃ̖��L���K�v�Ȑ������������邱�Ƃ������m���Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�����Ƃ��邱�Ƃ̈Ӗ��͕�����܂����C�C���̎d�������������ł��D�Ȃ��C�u�_�𐔒�����Ŏ����Ȃ���.�i�}�E�X�ŃN���b�N�j�v�͏����Ă���܂��D
���m�ʂ̕ł���̎���ɑ���n[���̐��E���̐��ɂ��ā^21.08.27
���ɓK�Ȑݖ�ł��B�w�E���鎖���͌�����ӏ��͂���܂���B
5�₷�ׂē�������܂����B
�L�������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�A���������i���Z�������j�ɂ��ā^21.08.25
�������肪�����ĕ��ɂȂ�܂����B�@���肪�Ƃ��������܂����I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�A���������̍���������͑��ɂ��ā^21.08.23
���퐶���Ɋ֘A�����A���������͂���܂����H
�����m��ҁn�F�Ƃ������́C���w�Z�̐��w�̋��ȏ��ň����Ă���u�A���������̕��͑�v�Łu���퐶���Ɋ֘A���Ă��Ȃ������P��ł��������Ƃ�����̂ł����H�v
���m�ʂ̕ł���̎���ɑ���n[�O�����̒藝�̉��p�ɂ��ā^21.08.18
�ƂĂ�������₷���ėǂ������ł�!!
��1�̊w�Z�̐V���̏h�肪�����ĎQ�l�ɂ����Ē����܂����B(��︎�L��︎`��︎)
���肪�Ƃ��������܂�(*�L�ցM*)
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���W���_1�ɂ��ā^21.08.18
�������͑S�ē����悤�Ȗ��Ȃ̂ʼn�����ԈႦ�Ă������悤�ɕ��K�ł���̂ŗǂ������ł�😌
�����Ƃ���͓��ɂ���܂���🙇��️🙏
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���̂̕\�ʐ�(�~���C�p���C�~���C�p���̕\�ʐ�) �ɂ��ā^21.08.18
�l�����̐����̌���ۂɖ₪�����Ă���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�W�J�����ɂ��ā^21.08.17
�ƂĂ�������₷���ėǂ������ł��I
�����Č����Ȃ�A�J���t���ȃC���X�g����������ƌ��₷���Ȃ�Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������̕ό`�m���P�n�ɂ��ā^21.08.12
�����Ă�̂������ł�̂ɁA�H�ɂ͂���Ȃ��ł�
�����m��ҁn�F�u���߂� [�@�H�@] ���P�I�сC�����ĉE�̗�������P�I�тȂ����D�v�Ə����Ă����ˁD[�@�H�@] ���P�I�Ȃ���C��肪���܂�Ȃ��̂ŁC�̓_���ł��܂���D
���m�ʂ̕ł���̎���ɑ���n[�m��(���Z�������) �ɂ��ā^21.08.12
���������ĂȂ��āA���Ȃ��č̓_�ł��Ȃ�
�����m��ҁn�F�u���ȉ��̖��ł́C�}�E�X�ŃN���b�N���ĉ���Ή�����o�܂����C���Ȃ���Ή���͏o�܂���D�v�Ə����Ă����ˁI���Ȃ��̂悤�ȋ��𑗂��ė���̂́C�P��������������ɁC��ʂ����Ă��邾���̏ꍇ�ł��D���ō����������̈�����Ƃ͈Ⴂ�C����Ή�ʂ��������܂��D�����������Ȃ��悤�ɉ��������Ȃ���C���̓_���o�܂���D
���m�ʂ̕ł���̎���ɑ���n[���������ɂ��ā^21.08.10
���q�����������ł��Ȃ�������A���Ȃ��Ă������Ƃ������Ƃł����H
�����m��ҁn�F�A�����肪�Ƃ��D�قڂ��̂悤�ɍl���Ă�����Ă��悢�D�������C�����ł����邾���̏ꍇ�����������Ɋ܂߂čl���܂��D
�m�ł����n

�m�ł��Ȃ���n

�킩��₷��
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���l���E�X�̒藝�ɂ��ā^21.08.08
�i�ꕔ���j��Ђ̒��Ԃ����q����̒��w�Z�̏h����������Ƃ��č����Ă����ɑ������܂����B
���l���E�X�̒藝�Ɋւ�����Ȃ̂ł����A���͖��W�ɉ����Ȃ��������ݒ肳��A��������̂��Ă��܂����B �@
�O�O���Ă��u����͉����Ȃ���ł���B�v�Ƃ��܂��o�����A��Ђ̃G���W�j�A�u���O�������^�C�~���O���������̂ŁA������ƍӂ����`�Œ��q�ł��������Ă݂܂����B
���[�������o�����Ă���Ȗ����o����������������ƒm���Ă��炨���Ǝv���āA�s�^�����m�Ń��[�����������Ē����܂����B���W�̉ɂ� x, y�Ƃ��l�������Ԃł����B
��낵��������A�����������B
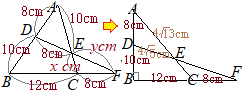 �����m��ҁn�F
�����m��ҁn�F�A�����肪�Ƃ��D���l���E�X�̒藝����́C�����̒����́u��v�����܂�C�K�����������̒��������܂�킯�ł͂Ȃ��̂ŁC������Ƃ��肾�Ǝv���܂��D
�Ȃ��C�x�N�g���╡�f����p���āC���W���v�Z����ɂ́C
���̃y�[�W���Q�l�ɂȂ邩������܂���D
�����ɑ��݂�����P�����������̂����Ɓi���p�O�p�`�ɂ��č��W�v�Z���y����j�C�Q�l�}�̂悤�ȗႪ���蓾�܂��D
(8)�̖��
����Z�̖�������ė~����
�����m��ҁn�F�A�����肪�Ƃ��D����Z�Ƃ������Ƃ����̊���Z��\���Ă���̂��H
���m�ʂ̕ł���̎���ɑ���n[�S�����i�p�[�Z���g�j�ɂ��ā^21.08.06
������₷���A���J�ɐ������Ă��āA�����ɓ��e���ۂݍ��߂܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[A=B=C�^�̘A���������i�������j�ɂ��ā^21.08.04
�ƂĂ����J�ɐ������Ă���ď��������B
�܂����Ȃ萔�w�I�Ȑ��������������̂ł������������Ăق���
����ǂƂł��킩��₷������
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�s�����̉������ɂ��ā^21.08.04
���ɕ�����₷���ł��B���N�̕s���_���������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D����ے��̉����ɔ����C���w�Z�łP���s�����̉������������āC���Z�ł��P���s�����������Ȃ��Ȃ��āu����Ȃ��Ƃ����Ă�����C������Ȃ��Ȃ鐶�k���o�ė���ȁv�Ǝv���Ă��܂������C�Ă̒�ł��D���Ȃ���������ł͂Ȃ��Ǝv��
���m??���^������^21.08.03
http://www.geisya.or.jp/~mwm48961/math/equat03.htm
���݂܂����B
����ł��B
1/(a-b)-1/(c)=d ������܂���B�i�j�͂킩��₷���悤�ɂ��������B�Ӗ��Ȃ��ł��B������bcd+b+c/cd+1 �������̂ł����A���P��������Ȃ������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�ǂ̋��ȏ��ɂ��u�����Ǝ��v�u�������v�Ƃ������ڂ�����܂�--���w�P�N�ŏK���D�u�����Ǝ��v�Ɓu�������v�̈Ⴂ��������Ȃ��Ɩ�肪�����܂���D���ɁC�u�������߂�̂��v�Ƃ������Ƃ�����҂��͂�����ӎ����邱�Ƃ��d�v
���m�ʂ̕ł���̎���ɑ���n[�A���������i�����W���C�����W���̖��j�ɂ��ā^21.08.02
�����W���̂Ƃ���̐������ƂĂ�������₷�������ł�
���肪�Ƃ��������܂���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�m��(���Z�������)�ɂ��ā^21.07.29
�O�X����m�������ł����B�m���͐搶�ɕ����Ă����܂���������Ȃ������̂ł����A���̃T�C�g�Ŋw�Ԃ��ƂŖ{���ɓ��ӂɂȂ�܂����B�������Z�̓������ł��̂ʼn�����ƒB����������܂����A�C���v�b�g�ƃA�E�g�v�b�g�̔䗦�����傤�ǂ����̂łǂ�ǂx���A�b�v����悤�ȃC���[�W�Ői�߂邱�Ƃ��ł��܂����B���肪�Ƃ��������܂����I
�Ō�ɁA�ꕔ�\�L�~�X�H�Ǝv���镔��������܂����̂ŏ����Ă����܂��B
�܂Ƌʂ̖��@���R�@⑵�@
�܂`����Q����o���Ƃ��C�N���蓾�邷�ׂĂ̏ꍇ�̐���N=3�~3=20�ʂ�D
�Ƃ����ӂ��ɂȂ��Ă��܂����B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m��茧/���̂�������n�^21.07.28
����ł��Ba��1/2(�a�{c)d�ŁC�a�ɂ��ĉ����ɂ͂ǂ��ɂ����炢���̂ł��傤��?
�����m��ҁn�F�A�����肪�Ƃ��D
d)
d)


�@�Ȃ��CB�����啶���Ȃ̂��ƁC�˂����݂����邩����
���̂��̉Ȃ����̂�������ė~����
�����m��ҁn�F�A�����肪�Ƃ��D�u�ǎ҂�����Ή�����o��v�u�ǎ҂����Ȃ���Ή���͏o�Ȃ��v�Ƃ����ݒ�ɂȂ��Ă��܂��D������C�P��������ɁC�������Ă��邾�����Ɖ���͏o�܂���
���m�ʂ̕ł���̎���ɑ���n[�������̍����ɂ��ā^21.07.26
���10�̉���̍Ōオ100�i���|7�j�ɂȂ��Ă���B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�ő���ƍŏ����{���ɂ��ā^21.07.19
�f�����������ł���悤�ɂȂ�܂����A�ő���A�ŏ����{�������Ƃ߂���悤�ɂȂ�܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�S�����i�p�[�Z���g�j�ɂ��ā^21.07.11
���肪�Ƃ��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝(�������)�ɂ��ā^21.07.11
���͂��������̓�Փx�ŁA����̐}�╶�͂��킩��₷���ėǂ������B
�܂��A�����F���ʂŕ����Ăق����B
�����m��ҁn�F�A�����肪�Ƃ��D���ׂ����ʂ����̋��ނł�
���m�ʂ̕ł���̎���ɑ���n[�P���������̉������ɂ��ā^21.07.09
������Ȃ��Ƃ����������₷���������Ă���ƂĂ��ǂ������ł�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�A���������i���Z�������j�ɂ��ā^21.07.06
������������o���Ăق����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[��@�̌���(a�}b)2�ɂ��ā^21.07.05
�킩��₷���Ă��肪�����ł��B
���K�������������āA�o����̂ɍœK�ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�O�p,���p�`�ɂ��ā^21.07.05
�ǂ�����
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Q�_�Ԃ̋����̌����ɂ��ā^21.07.04
���Ђ傤�̏�����������v�Z���Ă������H
�����m��ҁn�F�A�����肪�Ƃ��D�Ⴆ��
A(4, 5), B(1, 9)�̏ꍇ�C�r���̌v�Z��
^2%2B(9-5)^2})
�ƂȂ�܂����C
^2%2B(4)^2}=\sqrt{9%2B 16})
�̂悤�ɕ��̐��ł��Q�悷��Ɛ��̐��ɕς��̂ŁC�u������������傫�����������Ă����܂��܂���v
�uab��cd�@�́A���Ƃ��̊ԂɁ~���B��Ă��邩��@���~b��c�~���@����ˁH�v�Ƒ��q�Ɍ�����
�u����A�Ⴄ��v�Ǝv���A�ǂ����Ă����Ȃ̂������ł����ɍ����Ă��܂����B
�ucd�͂��łɈ�̐��ɂȂ��Ă���v�ƍl����̂ł��ˁI�@�������������肵�܂������A
�����Ƒ��q�����͊ԈႦ�Ȃ��Ǝv���܂��B���肪�Ƃ��������܂����I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�A���������̉������i����@�j�ɂ��ā^21.06.29
�����̏h��̎��ɉ��ɑ���@�̗Ⴊ�������̂Ō��Ă݂����ǂ悭������Ȃ��������璲�ׂČ��Ă݂���A(*�K0�K*)�X�b�S�b�C�I������₷�������ł��I���肪�Ƃ��������܂�😆
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������������ƂȂ邎�̒l�ɂ��ā^21.06.29
�������킩��₷���I�I�����Ƒ��₵�Ăق����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D���Z�����ɏo�����Ȃ��̂́C�قڐs�����Ă������ł��D���ꂾ�����Α��v
���m�ʂ̕ł���̎���ɑ���n[�����Ɛ����i�������j�ɂ��ā^21.06.25
�y���Q�z�i�P�j�ɂ��Ď��₪����܂��B
��3a���P���̎��R���ɂȂ邽�߂ɂ́A〖3a〗^�����鐔�̂Q��ɂȂ�K�v�����邩��A
�P���̎��R���Ƃ������ƂȂ̂ŁA1 �͂P���̎��R���ł��邩��
a^ =1/3 �̂Ƃ��A��3a=��(3�~ 1/3)=��1=1
a^���ǂ̂悤�Ȕ͈͂̐��Ȃ̂����蕶�Ŏ����Ă��Ȃ��̂�����A�����ł��悢�̂ł͂Ȃ�����
�l���܂����B
�����̒����������ɂȂ�������O���̂ŁA������a^ =1/3 ���v�����܂����B
�����u3, 12, 27�v�ł���Ȃ�A�ua^�͎��R���ł���v���Ƃ������K�v������Ǝv���܂��B
�܂��A����ɂ���
1/3≤a≤27 �E�E�E(1)
1≤a≤27 �E�E�E(2)
(1)����(2)�Ɉڂ�Ƃ��낪�킩��܂���B
(1)�̊e�ӂ��R�{����̂ł�����27���R�{���Ȃ���Ȃ�Ȃ��̂ł͂Ǝv���܂��B
���̕��s���ł�����\����܂���B���l�т��܂��B
�����m��ҁn�F�A�����肪�Ƃ��D���R���Ƃ������t�̓��̓~�X������܂����̂ŁC�������܂����D
���ɁC����������

�������܂��i3���|����Ƃ������ό`�ł͂Ȃ��u�����番����b�v�ł��j
�킩��₷���ł�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������ɒ������K�i���w�����j�ɂ��ā^21.06.24
0�E375
�����m��ҁn�F���ꂪ�ǂ������܂������H����Ȃ玿��ł��Ə����Ȃ��ƁD�����P�C�����_�͉p�ĕ����Ȃ�s���I�h�C�X�y�C���Ȃǂ̕����Ȃ�J���}�ł��D�����̓l�b�g�j���[�X�Ŏg���Ă��܂����C�w�Z�̐��w�ł͕s�ł�����|���Z�̏ȗ��L���ɂȂ�܂��D
���m�ʂ̕ł���̎���ɑ���n[�����v�Z�i���̒l�j�̓�������ɂ��ā^21.06.24
����������ł̏d�v�ȓ_��������ĂĂ킩��₷���B�����������̓��e����������Ȃ��̂ő��̎�ނ̓��e�̖����̗p���ė~�����ł�
�����m��ҁn�F�A�����肪�Ƃ��D���w�Z�̎��̒l�Ƃ������ڂ́C�����������܂���D���̓��e�͑��̍��ڂɂ���܂��DMac�Ō��Ă��邩��C���ɂ���T�u���j���[�������Ă��Ȃ��̂��ȁH
���m�ʂ̕ł���̎���ɑ���n[�A���������̕��͑�2�ɂ��ā^21.06.23
X�Ɓ~���������ɂ����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D���w�̊w�K�p�ɃQ�[���@��Nintendo WiiU���g���Ă���Ƃ������Ƃ̂悤�ł����C���ڂ���Ă���t�H���g�̎�ނ��Ⴄ��������Ȃ�������������CNintendo WiiU�Ő��w�̋��ނ��ǂ݂ɂ����Ƃ́C�N���N�ɉ��̋����q�ׂĂ���̂��H���Ƃ��Ɩ����Ȃ��Ƃ�����Ă��܂��D
���m�ʂ̕ł���̎���ɑ���n[�f���������̉��p1�ɂ��ā^21.06.23
�����������̐����~�����ł�
�����m��ҁn�F�A�����肪�Ƃ��D�u�f���������̉��p1�v���ς̂Ȃ�u�f���������̉��p2�v���������悢�̂ł́H
���m�ʂ̕ł���̎���ɑ���n[�������̕\�����ɂ��ā^21.06.20
�ʔ����Ȃ��ł��B�����Ɗy���������ɂ��Ăق����ł��B
�����m��ҁn�F���y�̎��ԂȂ炻��������邩��
���m�ʂ̕ł���̎���ɑ���n[�S�����i�p�[�Z���g�j�ɂ��ā^21.06.20
0.5(�S����)
�����m��ҁn�F50%
���m�ʂ̕ł���̎���ɑ���n[�������̕\�����ɂ��ā^21.06.20
�A���t�@�x�b�g����ɗ���v�Z����������
�����m��ҁn�F�A�����肪�Ƃ��D���ꂪ�ǂ������܂������H�ŏI�`���p��N�ia1�j�������ib3�j�ɂȂ�̂͂悭�Ȃ��ł����C�r���̌v�Z���ł͂���ł��傤�D
���m�ʂ̕ł���̎���ɑ���n[�A���������̍���������͑��ɂ��ā^21.06.18
�킩��₷������
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���s���Ɗp�ɂ��ā^21.06.18
�ԈႦ���Ƃ��Ƀq���g�������Ă킩��₷�������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~�ɓ��ڂ���l�p�`�ɂ��ā^21.06.17
���Ɩ��ɗ�����
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���s���Ɗp�ɂ��ā^21.06.17
����Ȃǂ�������₷���ėǂ������ł�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������������ƂȂ邎�̒l�ɂ��ā^21.06.14
���w3�N�ł��B�ƂĂ��킩��Ղ��A�悭�������邱�Ƃ��ł��܂����B����Ȉӌ��ł����A��萔������2��������₵�Ă���������ƍX�ɓ��ɓ���Ǝv���܂����B
���̃y�[�W�̂������ŒZ�����Ԃŕ����邱�Ƃ��ł��܂����B���肪�Ƃ��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�P�����̌v�Z�ɂ��ā^21.06.14
�l��iPad�ł���Ă��ł����ǁAEnter�����ƃy�[�W�����Z�b�g����Ă��܂��܂��B����͂ǂ��ɂ����Ă��炦�܂����H�ł����璼���ė~�����ł��B�Ȃ���������Ă���݂����ł��߂�Ȃ����B
�����m��ҁn�F�A�����肪�Ƃ��DiPad�łȂ��Ă�Windows�ł�Enter�L�[���������瓖�R���Z�b�g�����ł��傤�D�̓_����Ƃ����{�^�����N���b�N����悤�ɂȂ��Ă��܂��D
���m�ʂ̕ł���̎���ɑ���n[�Q��C�R��̕����ɂ��ā^21.06.13
���ł����@����́I�I�I�@�߂����ᕪ����Ղ������ł��@
�w�Z�ŏK�����͂��Ȃ�ł�����������Y��Ă��܂�����
�Ȍ��ŕ�����₷�������ł��@�@�{���ɂ��肪�Ƃ��������܂���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[ �����̐����ɂ��ā^21.06.13
��ϐ\����Ȃ��̂ł����A�ߎ��l�̈Ӗ��A���ߕ������܂���������܂���c
�����m��ҁn�F�A�����肪�Ƃ��D���̃y�[�W�ɂ́u�ߎ��l�v�Ƃ����p��͂���܂���D���w���ɂƂ��Ă̋ߎ��l�C���w���ɂƂ��Ă̋ߎ��l�C�����@�̉��p�Ƃ��Ă̑�P�ߎ��C��Q�ߎ��Ƃ��������Ӗ��ł̋ߎ��l�̂��ꂼ��́u�P�̓��v�Ƃ��Ď������Ƃ͂ł��܂���D�Z��E�w�N�E�Ȗڂ��i���Ď��₵�Ă��������D
���m�ʂ̕ł���̎���ɑ���n[�����t���̐��̍��ɂ��ā^21.06.12
�f���炵���ł��ˁI�I�@�@������ӂ����������܂��������̂ŁA10��قǂ���ė��K�����Ă��������܂���(��)(��)
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����̕ό`�ɂ��ā^21.06.09
��ɖ�肪�����Ă悩�����I���ƁA���̃y�[�W�̓ǂݍ��݂������ď������
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�P���������̉������ɂ��ā^21.06.08
������₷���܂Ƃ߂Ă��Ă������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����̕ό`�ɂ��ā^21.06.04
[���̕ό`�͂Ȃ��K�v�Ȃ̂�]��[�ǂ̂悤�ȏ�ʂŕK�v�Ȃ̂�]���ڂ��������Ē��������ł�🙇🏻��️
���萔���|�����Đ\�������܂���B�B�B
�����m��ҁn�F�A�����肪�Ƃ��D�P�̗�Ƃ��āC�u���̎��ɑ�����ĕ����̌������炷�Ȃlj��p���J���Ă���v�Ə����Ă��܂��D���̗�́C����������ʂɑ������Ă���l���Ă��������D
���m�ʂ̕ł���̎���ɑ���n[�������ɒ������K�ɂ��ā^21.06.03
�ƂĂ��킩��₷���C�悩�����ł�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������ł������ɂ��ā^21.06.02
���������O���̂͂ł��Ă����̂ł����A�������ł�����ꍇ�A�����ԈႢ�����Ă����̂ł����A���������ă}�C�i�X1�ł�����@�Ƃ����l�����łł���悤�ɂȂ���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�A���������i���Z�������j�ɂ��ā^21.06.01
�Ӗ���������Ȃ������Ƃ킩��₷��
�����m��ҁn�F�A�����肪�Ƃ��D������Ȃ��l�͊�{��肩��n�߂�̂����ʂł��C���Ȃ��͓������̍Ōォ��n�߂Ă���C�������t�ł��D���ɂ���T�u���j���[�̈�ԏォ�珇�ɍU�߂čs���ƁC�ł���悤�ɂȂ�܂��D
���m�ʂ̕ł���̎���ɑ���n[�W�J�����@(x+a)(x+b)�ɂ��ā^21.05.31
���̐����킩��₷������
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���̓W�J�ɂ��ā^21.05.31
���߂Ă��̖��������܂����B
����s�����̔��f����������ł��B(�ԂƉJ)
�����������������A�܂邩�o�c���ɂ��ė~�����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[��Βl�ɂ��ā^21.05.28
��Βl���ł����������́A0.01��0����0�Ȃ̂ł����H
�����m��ҁn�F�A�����肪�Ƃ��D�����ł�
���m�ʂ̕ł���̎���ɑ���n[�����̎g�p�ɂ��ā^21.05.28
���4�̐ݖ╶�Łu����1�i���j������v�ł͕������̂Łu����1�i���j������v�̕����A�s��̕��Ƃ��ĕ�����Ղ��Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�Ӗ����ς��̂ŁC���̂悤�ɂ͂ł��܂���
���m�ʂ̕ł���̎���ɑ���n[�A���������̉������i����@�j�ɂ��ā^21.05.26
�ǂ�����Ďg���������킩��Ȃ������ł��B�ł����������̂͂ƂĂ��킩��₷�������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�u���߂ɋ�I�сA�����đI������I�тȂ����B�v�Ƃ́u���߂ɋ�I�сA�����đI������I�тȂ����B�v�Ƃ������Ƃł��D���ɓǂݕ��͂���܂���D
���m�ʂ̕ł���̎���ɑ���n[�������ɒ������K�ɂ��ā^21.05.26
3���̓�́A���ɂȂ�܂���
�����m��ҁn�F�A�����肪�Ƃ��D����Ε�����͂�������C���̎��₪����Ƃ͑z�肵�Ă��܂���ł����D�����œ�����Ƃ��C2��3=0.6666���
���w�Z5�N�̎��Ƃ��x��ł����H�����Ƃ��C���w�Z�̐搶�Łu2��3�Ŋ���Ȃ��v�Ƌ�����搶������悤�Ȃ̂Łi�����ŏ��Ɨ]����o���Ƃ��C�{���͏���0�ŗ]�肪2�j�C�ǂ������ǂ����ł����D
���m�ʂ̕ł���̎���ɑ���n[�������ɒ������K�ɂ��ā^21.05.25
�������ǂ������ł����K�ɂȂ�܂������肪�Ƃ��������܂���
�����m��ҁn�F�A�����肪�Ƃ��D
�����쌧�m�����J����^21.05.25
�������͓��ɋ��ȏ͂Ȃ̂ʼn��߂Ă����炢�����Ă��������ł����A�}�����p���Ă����ĕ���������舵���Ă���T�C�g�̒��ł���ԕ�����₷�������Ǝv���܂��B
����1��=���ƕ\�L���Ă������Ƃ������Ƃ̐������B��̂������Ƃ킴�킴���킸�ɁA�w��x�Ƃ��������Ε�����Ƃ��������ŋ^�₪�������܂����B���肪�Ƃ��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�P�����̕������ɂ��ā^21.05.23
�킩��₷���ĂƂĂ��悢�ł��B���肪�Ƃ��������܂�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���̒l�ɂ��ā^21.05.22
���������Ƒ���̌`�ł���X��x��t����̂��t���Ȃ��̂����肽��
�����m��ҁn�F�A�����肪�Ƃ��D����̈Ӗ����ʂ��܂���D
�Ⴆ�C(1)�̖��ŁCx=2�̂Ƃ�3x+1=
�ƂȂ��Ă���Ƃ��Cx=2����������C3x+1=7������7�����ł��D���̌�ɂ͉�������܂���D
���m�ʂ̕ł���̎���ɑ���n[�����̕ό`�i�������j�ɂ��ā^21.05.21
�S�Ă̖��ɂ��ꂼ��Ƃ�蒼��������A���������ׂ�����������Ă��ĕ�����Ȃ�����������悤�ɂȂ�܂����I�I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[A=B=C�^�̘A���������i�������j�ɂ��ā^21.05.21
�ƂĂ��ǂ��ł��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������̕\�����ɂ��ā^21.05.21
�ƂĂ����₷���B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�ω��̊����ɂ��ā^21.05.21
��y=a��x(a�͒萔)�ɂ��āAx�̒l�ƕω��̊������������Ă��āAa�̒l�����߂��肪�����̖��W�ɂ������̂ł���������肢�ł��܂����H
�����m��ҁn�F�A�����肪�Ƃ��D�{���C���̖��W��ǂނׂ��ł��傤�D����ŕ�����Ȃ���C���̖��W�͂��Ȃ��ɂ͍���Ȃ��Ƃ������Ƃł��傤�D
�i�Ƃ���ŁC��肪�����ĂȂ��Ɖ������Ƃ͂ł��Ȃ�����C����ɖ�������ĉ������Ƃɂ���j
�ω��̊�����m�Ƃ����D
}{x_2x_1}}{x_2-x_1}&chf=bg,s,fff9f9)


��Βl��3�ȏ�7�����̐����͂Ȃ�ł����H
�����m��ҁn�F�A�����肪�Ƃ��D���̃y�[�W�̋��ނ��ς܂��āC����ł��܂�������Ȃ�����C���₵�Ă���Ƃ������́C�\���ǂ܂��Ɂi�P���Q�b�Ŏ���܂ŏ����I����Ă��邩��j�����̏h��̓����Ă���Ƃ������Ƃ̂悤�ł��D�܂��C���̃y�[�W�̖����ς܂��Ă��玿�₵�Ă��������D
���m�ʂ̕ł���̎���ɑ���n[�������������ƂȂ邎�̒l�ɂ��ā^21.05.09
���1������g��Ŗ��12�܂ŏI��������Ɂu�H�v�Ƌ^��Ɏv�������Ƃ�����܂��B�������̐��l���������ɂȂ邽�߂ɁA���̐��l�����ʈ����ł���������A�����̌`�𐮐��ɂ��邽�߂ɕ��q�ɕ���̔{�����l������A���ĕ����1�ɂ����肷��Ȃǂ��Ď��R��n�����߂܂������A�����o����n�̒l�����ɍ������R�����Ǝ����K�v�͂���܂��B�Ⴆ�Ζ��(12)�ŁA
360=6^2�~10�ł��邩��An=10�̂Ƃ�360/n=(36�~10)/10=6^2�ƕ������ɂȂ�B
n�͎��R���ł��邩��An=1�`9�܂ł̎��R�������X�� 360/n �ɑ�����Ă��������ɂȂ�Ȃ�����A
n=1�`9�͓K���Ȃ��B
���������āA���߂�ł����������R��n��n=10�ł���B
�̂悤�ɁA�un�͎��R���ł��邩��A�E�E�E�v�̂P���������Ȃ��Ă��悢�̂ł��傤���H
�킩����Ă��邱�Ƃ͏����Ȃ��Ă��A���w�̂��Ƃ��킩���Ă��������鐔�w�̐搶�����̓_������̂ł�����K�v�Ȃ��̂��ȂƂ��v���܂����An=1�`9�̏ꍇ�ɂ͕������ɂȂ�܂���Ƃ������Ƃ�t��������̂��K�v�Ȃ̂��ȂƋ^��Ɏv���܂����B
��낵�����肢���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D10�̔{���łȂ���Ȃ�Ȃ��Əq�ׂĂ���̂�����C1�`9�̌����͕s�v�ł��傤�D�܂��C���w�Z�ł͕K�v������\�������Ƃ������t���T�O�������Ȃ��̂ŁC�\�����̌������ł��Ă��Ȃ��̂͌��_���Ƃ����͍̂��ł��傤�D�����܂ŗv������ΐ����҂����Ȃ��Ȃ�\��������܂��D�_�q���Ƃ��āC�u������v�u�䂦�Ɂv�u���������āv�Ȃǂ��g�����C���S�ȕ��͂ɂȂ��Ă��邱�Ƃ�v������̂łȂ��C����炵���v�Z���������Ă����āC�����������Ă���ΐ����ɂ���ł��傤�D
���m�ʂ̕ł���̎���ɑ���n[�����v�Z�i���̒l�j�̓�������ɂ��ā^21.05.05
���Q�̉���ɂ���悤�ɂ���ƁA�l�����߂��邱�Ƃ͂킩��܂��B�܂��A�u����������������ꂽ��A�Ȃ����ꂵ���̂��v��ǂ�ł݂�ƁA�S�����̒l���ȒP�ɋ��߂邱�Ƃ��ł��邱�Ƃ��킩��܂��B����������ƂP�������������藧���Ƃ͒��P�Ŋw�K���܂������A�܂��Q���������܂ł����Ă��܂���B���ȏ�������ƂQ���������́A�u�Q�������O�v�ƂȂ��Ă���̂Œl�����߂���̂Ƃ͈���Ă���悤�Ȋ��������܂��B
���́i�R�j�����̂悤�ɍl���܂������A���������Ă��܂����B
x^2-6x=x(x-6)�ƕό`���邱�Ƃ��ł���̂ŁA
x=3+��2�̗��ӂ���U��������
x-6=3+��2-6
x-6=��2-3
�����苁�߂�l��
x^2-6x=x(x-6)
=(��2+3)(��2-3)
=(��2)^2-3^2
=-7
���̂悤�ȓ��ł��ǂ��̂ł����H
�����m��ҁn�F�A�����肪�Ƃ��D����ł����ł�
���m�ʂ̕ł���̎���ɑ���n[���Ώ̂Ȑ}�`�ɂ��ā^21.05.05
�����ǂ������ł��B
���w���̂�����Ȃ��ł��B(�K���ĂȂ������������炷�݂܂���B)
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�P�����Ƒ������ɂ��ā^21.05.05
��x�͒P�����ł͂Ȃ��̂ł����H
�����m��ҁn�F�A�����肪�Ƃ��D�u�����Ŋ����Ă�����́F1/2 x=0.5x���P�����v�ƐԘg�̒��ɏ����Ă���܂��D�u����ł͂Ȃ��̂ł����H�v�͔���I�Ȍ������ŁC�{���ɏ����Ă��邱�Ƃ�I�Ɏ��グ��̂́C���������ł��D�����Ƃ��C���{��E�����E���ȁE�J�i������Łu��x�v�Ə��������̂͂Ɛq�˂Ă���̂ł�����C�ʂ̘b�ł�����ǂ����̖����̕����K���Łu2%�v�Ə����Ă͂����Ȃ��D�K���u�Q�p�[�Z���g�v�Ə����Ȃ���Ȃ�Ȃ��D�ux/2�v�Ə����Ă͂����Ȃ��D�K���u��x�v�Ə����Ȃ���Ȃ�Ȃ��D�Ƃ����悤�ȕ����Ȃ��
���m�ʂ̕ł���̎���ɑ���n[���l���E�X�̒藝,�`�F�o�̒藝�ɂ��ā^21.05.03
������₷��
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�P�����̃O���t�̏������ɂ��ā^21.05.02
������₷��������肪�Ƃ��������܂��I�m�̃e�X�g�ŕ�����Ȃ������������̂ł����A���̃T�C�g�ŕ�����悤�ɂȂ�܂���😭😭���ꂩ�����낵�����肢���܂�🥺
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������̕\����.��������ɂ��ā^21.04.27
���z�łȂ��ׂ����w�E�Ő\����܂��A��3��3�Ԗڂ̎��Łi3.1�f�j�̂Ƃ��낪�i6�j�ɂȂ��Ă��܂�
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�����̕ό`�ɂ��ā^21.04.27
�����̕ό`
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����i�S����,����,�����j�ɂ��ā^21.04.24
�y��������
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�_�Ώ̂Ȑ}�`�ɂ��ā^21.04.24
������₷����`�`⤴�ȒP��������`⤴�}�`��]�������Ƃ��̐}�`����������I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�w���@���ɂ��ā^21.04.23
���������₷��
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�P�����Ƒ������ɂ��ā^21.04.23
�ƂĂ��A�킩��₷���ėǂ������ł���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�f���������ɂ��ā^21.04.21
�������肪�Ƃ��������܂��B
������₷��������Ă����Č��₷���ł��B
�����Ȃǂ�������Ă���̂Ŗ{���ɂ��肪�����ł��B
�ׂ������ƂȂ̂ł�������������萔�𑝂₵�Ă��S�R�ǂ��Ǝv���܂��B
�{���ɂ��肪�Ƃ��������܂��B �������炵�܂����B
�����m��ҁn�F�A�����肪�Ƃ��D���͂��Ă��˂��ŁC�ǂޕ��������������ł��D���Ė�萔�̌��́C���j���[�����ǂ��ĕʃy�[�W�����Ă����������Ƃ������߂��܂�
���m�ʂ̕ł���̎���ɑ���n[�P�����Ƒ������ɂ��ā^21.04.21
���܂蕶�͂��������Ă킩��Ȃ�����
�����m��ҁn�F�A�����肪�Ƃ��D���w�Z�̍��Ɂu�앶�������Ȃ����v�ƌ���ꂽ�Ƃ��ɁC�X���X���Ƙb�������Ƃ����e�p�������܂��Ă������̎q�������D���̕��́C�c��B���ƌĂ�������̒m�\���������ӂ������悤�ł��D�앶�����ӂȎq��A�����D�ʁD���̂悤�ɁC����\�͂����B���Ă���l�ƁC��I�Ȑ���}�`�̏��������ӂȐl���i�����̐l���j���܂��D
�@���ۂ̏��C���̕��͕��͂������Ɠǂ݂Â炢�̂ł����u�����ƌ��t�Ő������Ă����Ȃ��ƕ�����܂���v�Ƃ����l������̂ŁC������ɂ����킹�Ă��܂��D
���m�ʂ̕ł���̎���ɑ���n[��Βl�ɂ��ā^21.04.17
0.1�̏ꍇ�̐�Βl��������܂���B
�����m��ҁn�F�A�����肪�Ƃ��D0.1�ł�
���m�ʂ̕ł���̎���ɑ���n[�s���� �P�ɂ��ā^21.04.15
(3),(4)�̉��̐��������������ă}�E�X�ł��܂��������A�ԈႢ�ɂȂ�₷���B
�����m��ҁn�F�A�����肪�Ƃ��D���������ł́C���̂܂ܗ]�T�łł��܂��D�������������Ǝv���Ƃ��� CTRL+�u+�v �i�������͗v��Ȃ��j�ł�
���m�ʂ̕ł���̎���ɑ���n[�P�����Ƒ������ɂ��ā^21.04.15
5-2�͑������Ƃ����Ă������ł���
�����m��ҁn�F�A�����肪�Ƃ��D�����Q���邩�瑽�����ł��D�������́C�u���ލ����ȒP�ɂ���v�Ƃ����ό`���ł���̂ŁC��������3�ɕό`���܂��D
���m�ʂ̕ł���̎���ɑ���n[�������g�������m���P�n�ɂ��ā^21.04.01
�_������L���O�Ȃǂ��A���Ă��ꂽ������Ɗy�����o����Ǝv���܂��B����A���肢���܂�(>�l<;
�����m��ҁn�F�A�����肪�Ƃ��D
���̃y�[�W�Q��
������₷���A������Ȃ��l�̂��߂ɕ�����₷����������Ă���B������Ɩ��E��������ł܂Ƃ܂��Ă�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�f���������̉��p�ɂ��ā^21.04.01
150�ɂł��邾�����������R���������āA���̌��ʂ��A���鎩�R���̓��ɂȂ�悤�ɂ������B�ǂ̂悤�Ȑ���������Ηǂ��ł����B
�����m��ҁn�F�A�����肪�Ƃ��D���̃y�[�W�̖���������l�́C���̂悤�Ȏ�������Ȃ��͂��ł��D���̎��������Ƃ������Ƃ́C�܂��P�������Ă��Ȃ��\������ł��D�ł͊撣���Ă��������D
���m�ʂ̕ł���̎���ɑ���n[�����̕ό`�ɂ��ā^21.03.31
���ɂ킩��₷�������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�_�Ώ̂Ȑ}�`�ɂ��ā^21.03.30
����������ƈ��łƂ����傫�����āA�ł��₷�����Ăق����ł��B�悭�C���C������̂ł�낵�����肢���܂��I���ƁA����ȊO�͂ƂĂ������Ǝv���܂��I
�����m��ҁn�F�A�����肪�Ƃ��D�u�g�єł͕ʕŁv�Ə����Ă�����
���m�ʂ̕ł���̎���ɑ���n[�P�����Ƒ������ɂ��ā^21.03.30
���ɂȂ�܂����B
���肪�Ƃ��������܂����I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�P�����Ƒ������ɂ��ā^21.03.30
���R�́@�Q
�[�̓������ĂȂ�ł����H
��
�����m��ҁn�F�A�����肪�Ƃ��D���̃y�[�W�̏��߂̕��ɏ����Ă���܂��D�˕�����
���m�ʂ̕ł���̎���ɑ���n[�������ɒ������K�ɂ��ā^21.03.29
�������Ɏ������@�����܂����������ĂȂ������̂łƂĂ�������₷���������Ă��藝���o���܂����B
����Ɩɂ��Ă��������Ă��Ȃ������̂ŗ����o���܂����B
���N���w���ɂȂ閺�����S���ĕ��Ɏ��g�߂����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�w���@���ɂ��ā^21.03.25
���Z�̓��w�O�ۑ�ŁA�킩��Ȃ��Ƃ��낪���肱�̃T�C�g���J�����̂ł����������킩��₷�������ł��B�ƂĂ�������܂���😁���ꂩ������̃T�C�g�ɂ����b�ɂȂ낤�Ǝv���܂���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����}�`�����������ɂ��ā^21.03.25
���̃y�[�W�̉E��Ŏ�����Ă��遢ABE�Ɓ�DCE������AD�ƒ���BC��ɂ��ꂼ��̕ӂ���v�����Ȃ����AEB�Ɓ�DEC�Őڂ��Ă���}���瑊���}�`�f����Ƃ��AAB//CD�Ƃ���������������Ă���ꍇ�ɂ͕��s���̍��o�����������Ƃ����A=��D�A��B=��C�Ƃ��������������g���ā�ABE�Ɓ�DCE�������Ȑ}�`�ł���Ɣ��f�ł��܂����A����AB//CD�Ƃ���������������Ă��Ȃ��ꍇ�ɂ́A���w�P�N���Ŋw�K�����}�`�̈ړ��̎d������A�_E����]�̒��S�Ƃ��ĉ�]�ړ�������ƁA��EB�ƕ�EC���A��EA�ƕ�ED�����ꂼ�ꓯ���ɏd�Ȃ�̂Ł�ABE�Ɓ�DCE�������Ȑ}�`�ł���Ɣ��f���Ă��悢�̂ł��傤���B�Ή�����i�Ɣ��f�ł���悤�ȁj�ӂ̒�����ӂ̔䂪������Ă�������̐��l�̔䂩�画�f�ł��܂����E�E�E�B���w�͏K���������i�����ł͉�]�ړ��ł��j�𗘗p���Ď��̍l����i�߂Ă������̂��Ǝ��͊����Ă��܂��B
�����m��ҁn�F�A�����肪�Ƃ��DAB��CD�����s�łȂ��ꍇ�ɑ����}�`���ł���̂́C���ɂ͂P��
���̃y�[�W�ŕ��ׂ��̒藝�y���P�z�����ł��D
�u(4)�@�|�̉��Z�i�����Z�C���@�j�Ƃ��̌��ʁi���j�v�łQ�Ԗڂ�(+3)�|(+2)�̈ړ��ƌ��ʂ��P�ԖڂƓ����ɂȂ��Ă��܂����A�Q�Ԗڂ�(�|3)�|(+2)�ł͂Ȃ��̂ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��D��ł����C�������̂�����͕̂ςł��̂ŁC�������܂���
���m�ʂ̕ł���̎���ɑ���n[���w������̃v���O���~���O6.2�ɂ��ā^21.03.21
100m�i��
�E��120���������
100m�i��
100m�i��
����120���������
100m�i��
����60���������
100m�i��
�ł��߂ł����H
�����m��ҁn�F�A�����肪�Ƃ��D�O�p���̒l��������R�ʂŃY���Ă��܂����̂Œ������܂���
���m�ʂ̕ł���̎���ɑ���n[�l���v�Z�̗D�揇���ɂ��ā^21.03.17
9��3(4-1)�̏ꍇ�A�@�i�j�����v�Z�A9��3���v�Z�B3�~�i3�j���v�Z�ō����Ă��܂��ł��傤��
�����m��ҁn�F�A�����肪�Ƃ��D������ς��������̓���̖�肪���x���o����Ă��܂�.
�Q�N�O�̉������Ă��������D
������₷���������Ē������肪�Ƃ��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���̐��E���̐� �P���ɂ��ā^21.03.06
�����������Ǝv���܂���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�ڌ��藝�ɂ��ā^21.03.06
��肪���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���E�����i�������j�ɂ��ā^21.03.06
�ƂĂ��y���������ł��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Q���������̓�������ɂ��ā^21.03.05
�������̕��͑�͈����Ă��Ȃ��̂ł����B
�悭������Ƃ��ẮA�����`�̎��͂̒����Ɩʐς���A���ĂƉ��̒��������߂���Ȃǂ�����Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�܂��̂悤�ł�
���m�ʂ̕ł���̎���ɑ���n[�l���v�Z�̗D�揇���ɂ��ā^21.02.26
�|���Z���ɂ�闝�R���ڂ��������Ă��������B
�����m��ҁn�F�A�����肪�Ƃ��D���w�Z���w�̂ǂ̋��ȏ������Ă��C�u�|���Z���ɂ�闝�R�v�������ĂȂ��Ƃ������Ƃ́C�����Ȃ������悢�Ƃ������Ƃ��ƍl�����܂��D���̂悤�ȁu�K���v�����߂����炻���Ȃ��Ă��āC�u���̋K���ɏ]���Ďl���v�Z�����m�ɂł��邱�Ɓv���C���w���Ƃ������B�i�K�ɉ������ł��d�v�Ȃ��ƂŁC���R���ق������Ă���������̂��Ȃ��C�t�ɍ�������Ƃ������Ƃ�������܂���D
�@���w���łȂ���C�����Ă��\��Ȃ��̂ŁC�u�����v�����ƁF�l���v�Z�i�{�C�|�C�~�C���j�́C3+4, 3-4, 3�~4, 3��4�̂悤�ȓ��Z�i�Q�̍��̊Ԃ̌v�Z�j�Ƃ��Ē�`����Ă���C�{����3+4+5, 3-4-5, 3�~4�~5, 3��4��5�̂悤�ȎO�����Z�́C�ŏ��̒�`�Ƃ��Ă͑��݂��Ȃ��D�������C���ʂ̒����Ɍv�Z����Ƃ��āC�Ⴆ��(3+4)+5��3+(4+5)�̂悤�ɂǂ�2�����Ɍv�Z���Ă��������ʂɂȂ�Ƃ��́C�v�Z�̗D�揇�ʂ��ȗ����āC�P��3+4+5�Ə����Ă����ʂɉe�����Ȃ��D���̎���́C3�~4�~5�ȂǁC�����Z�����Z�̑g�C�|���Z����Z�̑g�ł͂��ł����藧�D
�@�Ƃ��낪�C�����Z�Ɗ|���Z�̑g�ł́C�Ⴆ�C(3+4)�~5=35��3+(4�~5)=23�̂悤�ȏꍇ�͌��ʂ��ς��̂ŁC�P��3+4�~5�Ə����ꍇ�ɂ́C3+(4�~5)��\���Ƃ����`�ŗD�揇�ʂ����߂Ă����K�v������D�t�Ɍ����ƁC�˂ɓ��Z�������s���C3���ȏ�̉��Z���s���Ƃ��͕K�����ʂ�t���ėD��W�������ꍇ�ɂ́C���̂悤�ȋK�����s�v�ƂȂ�D���̑���ɁC1+2+3��1�~2+3�̂悤�ȕ֗��ȏ������͂��ׂċ֎~�����s�ւȐ������������邱�ƂɂȂ�D
���m�ʂ̕ł���̎���ɑ���n[�S�����ɂ��ā^21.02.25
61�̒j���ł������������̉��p�ł��̃T�C�g�ɓ���܂����B���݂Ă������ł��Ȃ���������A���̃T�C�g�ɂ͒��w���w���݂����Ă������Ƃ���A���߂Ē��w���w����w�т����Ǝv�������܂����B�ƂĂ��e�ȓ��e�ŁA��������m�[�g�ɏ����ʂ��Ċw�K�������Ǝv���܂��̂ŁA���i�����肢���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�_�Ɛ��ɂ��ā^21.02.25
�ł�����傫�����Ă��������B��낵�����˂������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�g�傷��ɂ́uCtrl�v�Ɓu+�v���C�k������ɂ́uCtrl�v�Ɓu−�v���ɉ����܂�
���m�ʂ̕ł���̎���ɑ���n[�������̉������i��_�����j�ɂ��ā^21.02.25
������₷���Ă����Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝�ɂ��ā^21.02.24
���肪�Ƃ��������܂��A�v���o���܂���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���̂̕\�ʐ��ɂ��ā^21.02.23
�~���̕\�ʐς̖��̉łR�̂Q��Ə����Ă���܂���3�~2����Ȃ��ł����H
���a�~���Ǝv����ł�����ǂ��Ⴂ�܂����H
�����m��ҁn�F�A�����肪�Ƃ��D�Ⴂ�Ƃ��ɊԈ�������Ƃ��o���Ă��܂��ƁC��Œ����̂ɋ�J���邱�Ƃ�����܂��̂ŁC���̂����ɐ��m�Ȋo���������܂��傤�D�Ⴆ�Ύ��̂悤�Ɂu���̌`�v�ɉ����Ĕ��a

�̂P�����C�Q�����C�R�������Ή�����Ɗo����ƈ�ۂ������Ȃ�C�Y��Ȃ��Ȃ邩������܂���D
(1)�u���a�̒����v�u�~���̒����v�̂悤�Ȓ����͔��a

�̂P�����ɂȂ�D
���a�̒���

�C�~���̒���

(2)�u�~�̖ʐρv�u���̕\�ʐρv�̂悤�Ȗʐς͔��a

��2�����ɂȂ�D
�~�̖ʐ�

�C���̕\�ʐ�

(3)�u���̑̐ρv�̂悤�ȑ̐ς͔��a

��3�����ɂȂ�D
���̑̐�

��ɕK�v�ł͂Ȃ�
�����m��ҁn�F�A�����肪�Ƃ��D�w�K�w���v�̂̉����ɔ����āC�^����ꂽ�Q�̐������C3>1�̂悤�ɕs�������g���ĕ]�����邱�Ƃ܂ł����w�Z���w�͈̔͂ƂȂ��āC3+x>1�Ƃ����s�������������Ƃ͋��ȏ��ɍڂ�Ȃ��Ȃ�܂����D���������Ӗ��ł́u�K�v�Ȃ��v�Ƃ������������ł��܂����C����ł͎��Ԃɍ���Ȃ��̂ł��D
�@�܂��C������эZ�ł́C���w�̕����ƍ��Z�̕������Ȃ�ׂ��P��ŋ�����悤�ɂ���̂ŁC�u3+x>1�Ƃ����s�����̉������v���K���܂�����K�v�ł��D
�@���ɁC�����̕��ʉȍ��Z�ł́C���w�Z�Łu3>1�̏��������K������C�P���s�����̉������͏K��Ȃ��D�Q���s�����̒��O��10���قǐG��Ă���ŏI���Ƃ������Ԕz���ɂȂ肪���ł��D���̌��ʁC�P���s�����ƂQ���s�����̌����I�ȑ���ɋC�t�����Ƃ��Ȃ��C���Z�P�N���I���Ă��܂����Ƃ�����܂��D�u−3x>1�Ƃ����s�����̉������͕�����Ȃ��܂܉߂��čs���܂��v�D���������������̂����Ԃ�����邽�߂ɁC���̋��ނ��K�v���ƍl���Ēlj��������̂ł��D
���m�ʂ̕ł���̎���ɑ���n[���ލ��ɂ��ā^21.02.19
�r�����������鍀�ڂ��ق����ł��B�ƂĂ��킩��Ղ�������肾�Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����̐��ɂ��ā^21.02.19
���ɂ����ł�
�����m��ҁn�F�A�����肪�Ƃ��DMicroSoft�Ђ�Internet Explorer���g���̂́u������߂悤�v�ƌ����Ă���悤�ł��D���̋��ނ��Ή����Ă��܂���DChrome�œ_�����Ă��܂��D
���m�ʂ̕ł���̎���ɑ���n[���̒��ɂ��ā^21.02.19
�y���������ł��B
�����Ƃ�肽���ȁB
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�O�����̒藝(�O�p�`�Q�̖��2)�ɂ��ā^21.02.19
�߂��ᕪ����₷��
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�W�J����(a+b)2�ɂ��ā^21.02.19
�����v�����P���ׂ��_�́A�v�Z���ŋL�����鍀�ڂ����������Ȃ̂��A+��|�Axy�Ȃǂ̕����ƕ������L���ł���悤�ɂ��邱�Ƃł��B�������邱�ƂŁA�����ȃ~�X(�����̊|���Z�̊ԈႢ�A����xy�Ȃ�)�ւ̗��K�ɂ��Ȃ�Ǝv���܂��B�܂��A���x�����Ƃɕ����āA���ꂼ��œ�����S�Ď����ŏ��������݂̂܂܂ʼn������ȂǑI�ԂȂǂ��Ă������Ǝv���܂��B
���̃T�C�g�͂ƂĂ��킩��Ղ������Ǝv���܂��B�撣���Ă��������B
�����m��ҁn�F�A�����肪�Ƃ��D�L�������ɂ��āF���̋c�_�͂悭����܂��D����S���w�̊ϓ_������C�I��������L�������̕����w�K�҂̐ϋɐ��������o���₷���Ȃǂ̐�������܂��D�Ƃ���ŁC���w�Z�ȏ�̐��w�̓��Ăł́C�u�������ǂ��̓_����̂��v�Ƃ����傫�Ȗ�肪����܂��D(1) �����������p�����i�P�o�C�g�����j�����͂ł��Ȃ��@�킪���饥��^�u���b�g�łƂ��ǂ�����悤�Ȋ���.(2) x, X, ��, �w�̂悤�ɂP�̕����ɑS�p���p�C�啶���������̂S�ʂ肪����C�ǂꂩ�𐳓��ɂ���Α��͌듚�ɂ��Ȃ���Ȃ�Ȃ����C�ǎ҂͂Ȃ��듚�Ȃ̂������ł��Ȃ����Ƃ�����D(3) ���������̒v���I�Ȃ��ƂƂ��āC��ʂ̓ǎ҂�

�ȂǂƏ������Ƃ��ł��Ȃ��D��������������ƁC�܂��K��������̊w�Z�̓��ĂɁCx*y �Ƃ� x^2 �ȂǂƏ����Ă��܂��D(4) �Ⴆ�C

�������̏ꍇ�C

�C

�ȂǏ����̈قȂ�6��ނ̂ǂ��܂ł����e�͈͂ɂ��邩�D(5)

�̂悤�ɕ����ԂɃX�y�[�X�������Ă���ꍇ�Ȃǂ̋��e�͈͂ȂǍ̓_�̂��߂ɕK�v�Ȗ������߂Ă��C���w���ɂ͉��̘b�Ȃ̂��������ł��Ȃ��D���(1)(2)(5)�Ȃǂ́u�Ⴄ�����������Ă��铚�ẮC����ɒ����Đ����ɂ��Ă��܂��v�Ƃ����v���O�����ɂ��邱�Ƃ��ł��܂����C���̂悤�Ȃ��Ƃ�����Ɓu�����������̂��߂ɋL�q���ɂ����̂��v�Ƃ����˂炢�̂قƂ�ǂ������Ă��܂��D
�@���������킯�ŁC�����_�ł��̋��ނ̕M�҂́u�I������v�u�ȒP�Ȑ��l�݂̂̋L�������v�ɌR�z���グ�Ă��܂��D���(6) ���̑��CIphone�Ȃǂ̃X�}�z�ł́C�X�N���[���^�b�`�L�[�{�[�h���o���Ă��܂��ƁC���ނ����������Ȃ��Ȃ�Ƃ�����_������C������v���I�ł���������C���k��70%�ȏ�͂o�b�ł͂Ȃ��X�}�z���狳�ނ�ǂ݂܂��D(7) �����ϊ��ȂǑ�����@�̔ς킵���́C�X���[�Y�Ȏv�l��W���܂��D
�@�ȏ�̂悤�ɁC���Ȃ��̍l���́u�w�Z�Ŏ��ɓ��Ă������ꍇ�Ɂv�悢�l���ł����C�l�b�g�ʼn���ꍇ�ɂ̓}�C�i�X�ޗ��������̂ł��D
���ɂȂ�܂���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[��@�̌����ɂ��ā^21.02.11
����ł��B
���́A�u�W�J����v�Ƃ������t�̒�`�́u�������̐����̐ς̌`�����������v�Z����, �P�����̘a�̌`�ɂ��邱�Ɓv�Ɨ������Ă��܂��B�Ⴆ�A�P�������m�̐ς͂��̒�`�����Ă���̂ŁA�P�������m�̐ς��v�Z����s�ׂ��u�W�J����v�ƌ����Ă��悢�̂ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D�W�J�̒�`�͂���ł悢�ł��傤�D������C�P�����̏�@�⏜�@�́C�u�P�����̏�@�⏜�@�v�Ƃ����C�W�J�Ƃ͂����܂�������C�����C�[�тƂ������Ȃ��Ă��܂�����Ƃ���ŁC���̏ꏊ�Ŋ撣���āC����������̂��ȁH�����͊撣��ӏ��ł͂Ȃ��悤�ȁH
���m�ʂ̕ł���̎���ɑ���n[�_�Ώ̂Ȑ}�`�ɂ��ā^21.02.03
�ƂĂ��킩��₷�������I������Ȃ��������������ɂ킩�����I���̐��Ȃǂ��lj����Ă��炦��Ƃ����Ɨǂ��Ǝv���I
�����m��ҁn�F�A�����肪�Ƃ��D�i���j�Ώ̂Ȑ}�`�ɂ͑Ώ̎�������̂Ŏ��̖{���Ƃ�����肪����܂����C�_�Ώ̂Ȑ}�`�ɂ͑Ώ̂̒��S�͂���܂����C�Ώ̎��͂Ȃ��̂ŁC���̖{���Ƃ������͂���܂���D
���m�ʂ̕ł���̎���ɑ���n[�����v�Z(�������)�ɂ��ā^21.01.27
������2��̍H�v�̂������m�肽���ł��B��낵�����肢���܂��I🥺
�����m��ҁn�F�A�����肪�Ƃ��D�����ɏo�Ă�����x�̖��ł́C���Ɂu�H�v�v���o����K�v�͂Ȃ��C�P�ɂQ�悷��悢�ƍl������D
^2=\frac{2^2}{3^2}=\frac{4}{9}&chf=bg,s,fff9f9)
������q�̂Q���̂Q��Ŋ���
^2=(\frac{2}{3})^2=\frac{2^2}{3^2}=\frac{4}{9}&chf=bg,s,fff9f9)
������Ă���C�Q�悷��
^2=\frac{2^2}{3^2}=\frac{4}{9}&chf=bg,s,fff9f9)
������̐��̂Q��́C���̐��ɂȂ�
�����Ă��炢�������Ƃ�����܂�
�����m��ҁn�F�A�����肪�Ƃ��D�f���I�Ȏg�����̏ꍇ�C��ʂ̃��[���}�i�[�̂悤��,�P������=�u����C�ԓ��C����̈ꌾ�v�̊�{�ł͊Ԃɍ����܂���̂ŁC���ڂɎ�������������悢�ł��傤�D�������\���̎���Ȃǂ�����ꍇ�ɁC������������i�A�m�j�}�X�j�̏ꍇ�C�ǂ̎���Ƃǂ̎��₪����l���Ȃ̂����ƍ����Ȃ��Ă͂Ȃ�܂��C����͎�ԉɂ���ςȂ̂ł��D
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝(�������)�ɂ��ā^21.01.26
�A���������łȂ��q���g���o���Ă���������ƃX���[�Y�ɉ������Ƃ��ł���Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�e���̑O�ɗ��Ƃ����̂�����܂��ˁD����̓X���[�ł����H�������ɗ����Ă��܂��H
���m�ʂ̕ł���̎���ɑ���n[���l���E�X�̒藝,�`�F�o�̒藝�ɂ��ā^21.01.23
�������킩��₷���ł��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝(�������) �ɂ��ā^21.01.23
�����ǂ���肪�����ėL�������ł��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���ʊp�C���p�C�O�p�`�̓��p�̘a�C�O�p�̗��K����ɂ��ā^21.01.21
���͂���������̂��~�����ł��B�ƂȂ�̐Ԃ����̊G���킩��ɂ��������ł��B���ۂ̊G���Ƃ���Ă��������ɂ킩��܂������A��������������₷���G���ǂ��Ǝv���܂��B�B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝(�������)�ɂ��ā^21.01.19
������ƂĂ�������₷���ď�����܂����肪�Ƃ��������܂�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝�ɂ��ā^21.01.18
��̗Ⴊ�����Ă킩��₷�������ł��I�I
�܂����ז����܂��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���̂̕\�ʐ��ɂ��ā^21.01.18
�q���g���������������ڂ��������Ă���Ɨǂ��Ǝv��
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�H�����̔Z�x�ɂ��ā^21.01.17
���������ɗ����܂����I���肪�Ƃ��������܂�(ᐡ�B• · •�Bᐡ)♡
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Q���������̉������ɂ��ā^21.01.16
x²-5x�{6=0
�����m��ҁn�F�A�����肪�Ƃ��Dx²-5x�{6=0�̉��Ԉ���Ă��܂����Hx²-5x�{6=0���ǂ������܂������H�����ǂ��Ȃ̂�������Ȃ��ƁC�b���ʂ��܂���
���m�ʂ̕ł���̎���ɑ���n[�O�����̒藝�̉��p�ɂ��ā^21.01.15
�����Ǝv���܂���
����������������������肢���܂�🤲
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�S�����i�p�[�Z���g�j�ɂ��ā^21.01.12
150�p�[�Z���g�������ɂ���Ɖ��ł����H
�����m��ҁn�F�A�����肪�Ƃ��D�����i�l�������Ȃ����Ɓj→�����i�����_�̂��Ă��鐔�j
�S������100�Ŋ���Ə����ɂȂ�→1.5
���m�ʂ̕ł���̎���ɑ���n[�P�����Ƒ������ɂ��ā^21.01.12
3a�~2b�͑������ł����H
�����m��ҁn�F�A�����肪�Ƃ��D6ab�ɂȂ�̂ŁC�P���������������Ƃ������ł́C�P�����ł��D
���m�ʂ̕ł���̎���ɑ���n[�O�p�`�̓��p�̘a�ɂ��ā^21.01.11
�E�̐}���Q�l�ɂ��Ďl�p�`�ƌ܊p�`�̓��p�̘a�����߂Ȃ����D�l�p�`�̓��p�̘a��360�K�̖��œ�����ꏊ���l�p�`�ɂȂ��Ă܂�
�����m��ҁn�F�A�����肪�Ƃ��D�l�p�`�̓��p�̘a�����߂Ă���̂�����C�l�p�`�Ə����͉̂������͂Ȃ��ł��傤�D
�@����Ƃ��C�u�l�p�`�ƌ܊p�`�̓��p�̘a�����߂Ȃ����v�Ƃ́u��p�`�̓��p�̘a�łȂ���Ȃ�Ȃ��v�ƍl���Ă���̂ł����D�����ł́u�l�p�`�̓��p�̘a�v�Ɓu�܊p�`�̓��p�̘a�v�����߂Ȃ����Ƃ������Ƃ��u�l�p�`�ƌ܊p�`�̓��p�̘a�����߂Ȃ����v�Ə����Ă��܂����C���̂��Ƃ́C�}�ɂ���蕶�ɂ������ď����Ă���̂ŁC����Ε�����܂��D
���m�ʂ̕ł���̎���ɑ���n[���������ɂ��ā^21.01.10
����͉��肪�Ƃ��������܂����D
���͒�2�Ȃ�ł����A�w�Z����h��ŏo���ꂽ���W�̒��ɂ��̖�肪�����āA������悭�킩�炸���₳���Ă��������܂����D��w�����ɏo�郌�x���Ȃ�ł��ˁA�A�����ł��D
�܂����₷�邱�Ƃ����������낵�����肢���܂��D
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[ �~���p�̒藝(�������)�ɂ��ā^21.01.09
����ȂǐF��������Ă��ĂƂĂ������Ǝv���܂����A��肪�����Ɠ�����������Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���������ɂ��ā^21.01.09
4a^2b^2-(a^2+b^2-c^2)^2�@�̈��������̂����������ĉ�����.
�����m��ҁn�F�A�����肪�Ƃ��D���w���w�̃y�[�W���玿�₵�Ă���悤�ł����C���w�ł͂����������͂ł܂���D���Z�������̑�w�������ŏo�܂��D
���̃y�[�W�̖��2(1)�̉�[2]�̌�납��4�s�ڂ܂ł����t�ɂ��āi�Ō�̊��ʓ���b+c-a�Ƃ��āj�ǂ�ł�������
�f���炵��👏
�ƂĂ��킩��₷���ł�(*�L�ցM*)
�o����ΘA���������̍����̃R�c�Ȃǂ������Ă�������🙇
�����m��ҁn�F�A�����肪�Ƃ��D���¥�������Ȃ������Ă���y�[�W���R�c�ł�
���m�ʂ̕ł���̎���ɑ���n[�������̉������ɂ��ā^21.01.08
�������̃O���t�̕ψ�̋��ߕ����B���ł� �����Ă�������
�����m��ҁn�F�A�����肪�Ƃ� �u�������̃O���t�̕ψ�v�Ƃ����l�����͂��܂���̂ŁC���̃O���t�̕ψ�̍��ڂ����Ă��������D
�����Ƃ�
����
�ƂĂ�������₷���������Ă����������̂łƂĂ����ɂȂ�܂���❗️���肪�Ƃ��������܂�😄
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����̐����ɂ��ā^21.01.05
�t�@����₷���������x�C�x�[
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�P�����̃O���t(�W�J�`.�ؕЂƌX��) �ɂ��ā^21.01.05
http://www.geisya.or.jp/~mwm48961/math/m2line05.htm
�������i�W�J�`�j���ؕЂƌX��2
���̃y�[�W�́y��1�z�ɂāum2line05_illust1.png�v�Ƃ����摜�t�@�C�����\������Ă���܂���B
�C�������肢�������܂��B
2021.1.5
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�����̐��̐ρE���ɂ��ā^21.01.03
�����̐��~���̐��@�ɂ���
���w2�N�ł����Z�𑫂��Z�ŕ\�����Ƃ��̂悤�ɁA�����̐����A�E���̉��������A���̌��ʁA���̐���Βl�͐�Βl�̐ςɂȂ�B
�i��j (-2)�~3=(-2)+(-2)+(-2)
�Ƃ����������ł��܂��B
�����̐��~���̐��@�ɂ���
�E���̐���1���炷�ƁA�ς͍����̐�������������B
�i��j
4�~3=12
4�~2=8
4�~1=4
4�~0=0
4�~(-1)=-4
4�~(-2)=-8
4�~(-3)=-12
�i���̏ꍇ�A4�������j
�Ƃ����������ł��܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����ň͂܂ꂽ�}�`�̖ʐ��ɂ��ā^21.12.30
���K���Ƃ��Ďg�킹�Ē����Ă���܂��B���肪�Ƃ��������܂��B
���P�z
���̂Q����l, m��y���Ƃň͂܂ꂽ�O�p�`�̖ʐς����߂Ȃ����D
y=x+1 �c(l)
y=�|x+5 �c(m)
�̖��ł����A�����͂S�ł����łS��I�Ԃ�✕�ɂȂ��Ă��܂��܂��B�~�X���Ǝv���܂�����낵�����肢���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝(�������) �ɂ��ā^20.12.30
�ƂĂ��ǂ��A�֗��Ȃ̂ŁA�A�v���ɂ��Ă��炢�����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�A�h�C���C�A�h�I���\�t�g�ɂ��Ȃ��Ă��C�u���E�U��œ����Ă����炻��ł悢����
���m�ʂ̕ł���̎���ɑ���n[���̒l�ɂ��ā^20.12.30
������Ă��ꂽ�̂ŁA�����X���X���ł����̂ŁA�ƂĂ�������₷��������
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝(�������) �ɂ��ā^20.12.26
��@���킩��₷���Q�l�ɂȂ�܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
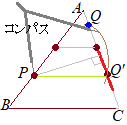 ���m�ʂ̕ł���̎���ɑ���n[���s���Ɛ����̔��ɂ��ā^20.12.24
���m�ʂ̕ł���̎���ɑ���n[���s���Ɛ����̔��ɂ��ā^20.12.24
�O�p�`ABC�ɂ����āAAB�̓����_��P�AAC�̓����_��Q�Ƃ���Ƃ��AAP:AB��PQ:BC��2:3�ł���̂ɁAPQ��BC�����s�ɂ͂Ȃ�Ȃ���̓I�ȗ�́H
�����m��ҁn�F�A�����肪�Ƃ��D���}�ɂ����āCP����AC�ɍ~�낵�������̑����ԂŎ������͈͂ɂ���CPQ'=PQ�ƂȂ�D���̂悤�ɃR���p�X�̒��S��P�ɒu���C���_��Q'���瓮������AC�ƌ����_��Q�Ƃ���Ƃ悢
���m�ʂ̕ł���̎���ɑ���n[�������������ƂȂ邎�̒l�ɂ��ā^20.12.21
���R�̕ʉ��Ƃ���
���Ƃ����̂͂Q���{�P�Ƃ��������ʂŐi��ł���̂ŁA��x=1�̂Ƃ��@2�̓��ł���S�ւ̑����ʂ͂R
2x�{1=19
2x=18
x=9 �ƂȂ�܂��B
���p�͂ł��Ȃ��Ǝv���܂����������̗�Ƃ��ďo���Ă݂܂����B�@��l�̒��R���B
�����m��ҁn�F�A�����肪�Ƃ��D���̓��Ă���́C

�̂Ƃ��C

�����獪���������ɂȂ�i�\�������j�Ƃ������Ƃ͌����܂����C����ȊO�ɉ����Ȃ����Ɓi�K�v�����j�������Ă��܂���D
�@�u�����v�̖��Ƃ������́C�u���̓W�J�v�ōl�������������Ղ��ł��傤�D�Ⴆ��
^2=x^2%2B 19&chf=bg,s,fff9f9)
���Ȃ킿
=19&chf=bg,s,fff9f9)
���������̂́C

�̏ꍇ�Ɍ���Ƃ������Ƃ������K�v������܂��D
�@���w���̓��ĂƂ��ẮC�悭�l�����Ă��܂����C���ĂƂ��č̓_����ꍇ�́C���w���ł����Ă����Z���ł����Ă��C�z�_�̂T�����炢�ɂȂ�܂��D
�@���w�ł́C�K�v�����C�\�������Ƃ����p����K���Ă��܂��C���ނɏ��������@�ł́i19�Ƃ��������̑f�����������P�ʂ�ł��邱�Ƃ��g���j�C���̂悤�ȓ�����ɓ��ݍ��ނ��ƂȂ��C���Ղɉ����܂��D
���̏�ō̓_�ł��ėǂ�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Q��C�������C���[�g�ɂ��ā^20.12.21
�p�\�R���ɂ�鐔�w�I�\���������Ă��������B�i��j�Q�̓��𐔊w�I�ɕ\�����@ �Q�́���ɕ\�����@ �����Ă��������B
�����m��ҁn�F�A�����肪�Ƃ��D�p�\�R���ƌ����Ă��C���p���ɂ���Ăł��邱�Ƃ��ς��܂��D
�Q�̓������߂邾���Ȃ�CGoogle�œd��Ɠ��͂���Ηǂ��ł��傤�DYahoo�I�Ȃ�2�O2�͂Ɠ��͂���Ό��ʂ��o�܂��D�Q�̃��[�g�����l�ł����u�����Ɂv�Ƃ͈Ӗ���������܂���D
������̐^�ӂƂ��ẮC���w�I�Ȍv�Z���p�\�R���ōs���ɂ́H�Ƃ������Ƃ̂悤�ł����C���̎��₪����Ƃ������Ƃ́CExcel�Ȃǂ̃\�t�g�̗��p���@��������Ȃ��Ƃ������̂悤�ł�����C�\�t�g���g�킸�ɂƂ����O��ʼn���ƁC��L�̂悤�ɐ��w�I�ɂ͖����ł�����Web�u���E�U�ɖ₤�Ƃ������ƂɂȂ�܂��D���̎����R�s�[���āC�e�L�X�g�G�f�B�^�i�������Ȃǁj��abc.htm�Ȃǂƃt�@�C���ɖ��O��t���ĕۑ����CChrome�Ȃǂ̃u���E�U�œǂ߂C�Q�́オ�\������܂��D�Ō��<�����Ă��܂���
<html>
<body>
<script type="text/javascript">
y = Math.sqrt(2);
document.write(y);
</script>
</body>
</html>
�ƂĂ��킩��₷�������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�O�����̒藝�ɂ��ā^20.12.18
3�����̒藝���g���ہA�p�x�̌��܂�͂���܂����H
�����m��ҁn�F�A�����肪�Ƃ��D���w�Z�̋��ނŁu�O�����̒藝�v�Ƃ����ꍇ�ɂ́C���p�O�p�`�̎O�ӂ̒����ɂ��Đ��藧�W�ł��D
�@���̏�ʂŁu�p�x�̌��܂�͂���܂����H�v�Ƃ����q�˕��͕���킵���̂ŁC�ʏ킻�������q�˕��͂��Ȃ��D���Ȃ킿�C(1)���p�O�p�`�ł������C���藧����u���p�O�p�`�ł������p�x�ɂ͐����͂Ȃ��v�Ƃ������܂��D(2)���p�O�p�`�łȂ���Ȃ�Ȃ�����C�P�͒��p�ŁC���̂P�̊p��0�������傫��90�������������Ȃ���Ȃ�Ȃ��Ƃ�������������Ƃ������܂��D
���m�ʂ̕ł���̎���ɑ���n[�Q�����̃O���t�ƒ����ɂ��ā^20.12.15
�ƂĂ��Q�l�ɂȂ�܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�O�����̒藝�̉��p�ɂ��ā^20.12.10
�����i�����͍����j�̑Ή������قȂ�ӏ�������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�ǂ̉ӏ��̑Ή����ǂ��Ԉ���Ă��āC�����̍l���铚�Ă͂������ƌ����悤�ɂ��܂��傤�D
�@���܂łɎ��ۂɂ������C���[�X�g����E�ӌ��́u�������̃y�[�W�ɊԈႢ������܂����v�Ƃ������̂ŁC�ǂ̃y�[�W�ɂǂ�ȊԈႢ������̂��������Ɂu�ԈႢ������v�ƌ����Ă��邾���̂��̂ł����D�_���I�ɏ������Ƃ��K�v�ȏ�ʂŁC�U�Ȃɖ���������\�����g���Ă��C���ۂɂ́u�S���������Ă��炨�����I�v�ƌ����Ă��邱�ƂɂȂ�C�Ή��ł��Ȃ����ƂɂȂ�܂��D
���m�ʂ̕ł���̎���ɑ���n[�_�Ώ̂Ȑ}�`�ɂ��ā^20.12.10
������₷������
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�H�����̔Z�x�ɂ��ā^20.12.9
�H�����̖��Ő��̋��ߕ��͂Ȃ�ł����H
�����m��ҁn�F�A�����肪�Ƃ��D�����Ƌ�̓I�Ȗ��Ŏ��₵�Ȃ��ƁC���₪���R�Ƃ��߂��Ă��܂��D
�@��ʓI�Ɍ����C�i�H�����̏d���j���i���̏d���j+�i�H���̏d���j������i���̏d���j���i�H�����̏d���j−�i�H���̏d���j�ŁC����܂łł��D�������C����͓��R�̂��ƂŁC���ȂȂ��̐q�˂������ƂƈႤ�ł��傤�D�u6(%) �̐H���� 100(g) �ɁC���� g ��������ƁC5(%) �̐H�����ɂȂ�܂����D�v�Ƃ������Ȃ�Ή��̕��ɂ���܂��D���̂悤�ɁC��̓I�Ȗ��������Ď��₵�Ȃ��Ɠ����i��Ȃ��̂ł��D
���m�ʂ̕ł���̎���ɑ���n[�A���������̉������i����@�j�ɂ��ā^20.12.9
�m���߂����A���������ɑ���@���lj����ė~�����ł��B
��낵�����肢���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D���̉��Ɂ���ŏ����Ă���܂��̂ŁC�����ǂ�ł��������D
���m�ʂ̕ł���̎���ɑ���n[���̃O���t�ɂ��ā^20.12.8
�킩��₷�������ł��B�@���肪�Ƃ��������܂����B
���ꂩ����撣���Ă��������B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������̕\�����ɂ��ā^20.12.3
(�S)�̓����Ŏ��₪����܂��A�Ȃ�������a�������Ȃ��ł����H�����Ă��������B
�����m��ҁn�F�A�����肪�Ƃ��D(�S)�Ƃ������͂�������܂��D�ǂ�(�S)�Ȃ̂�������Ȃ��ƈӖ����ʂ��܂���D
���2��(�S)�ł́C�u0a, 0x�Ȃǂ́C�P��0�Ə����܂��D�ǂ�Ȑ��ł�0����������0�ɂȂ邩��ł��D�v�Ə����Ă���܂��D����ɕt�������錾�t�͂���܂���D���5�́i4�j�ł�a�͏����Ă��܂���D���6�́i4�j�ł�a�̂P�͖ŏ����܂��D
���m�ʂ̕ł���̎���ɑ���n[��i�@�ŕ\�킳�ꂽ���̘a�ɂ��ā^20.12.2
�킩��₷��
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝�ɂ��ā^20.12.2
�߂����Ⴂ��
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝�ɂ��ā^20.12.01�n
���K��肪�����Ă߂����Ⴂ���ȂƎv���܂���‼
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������̕\�����ɂ��ā^20.12.01�n
����Z�̕\�������A�莝���̃K�C�h�A���W�ɂׂ͍����ڂ��ĂȂ������Ă��܂����B
�ƂĂ��킩��₷���A���K��������A��Ϗ�����܂����B���肪�Ƃ��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����̕ό`�ɂ��ā^20.12.01�n
���n�̍��Z�O�N���ł��B
���ό`�̊�b���ł��ĂȂ��Ă��̃T�C�g�ɒH�蒅���܂����B
���ɒT���S�����������ċC�����悩�����ł��I
�Q�l�����琔�w���܂��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������������ƂȂ邎�̒l�ɂ��ā^20.11.22�n
���̂�����������₷���ƂĂ����ɂȂ�܂���
���ꂩ������p�����Ē����܂�⸝⸝- ̫ -⸝⸝
���肪�Ƃ��������܂���🙇⋱��
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���Ώ̂Ɠ_�Ώ��ɂ��ā^20.11.22�n
�킩��₷��
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�ω��̊����ɂ��ā^20.11.21�n
�r�������Ȃ����番���肸�炢
�����m��ҁn�F�A�����肪�Ƃ��D���Ȃ��́C���̋��ނ̎g�������Ԉ���Ă��܂��D�u���[���F�������������I�����C�����ĉE�����炻�̓���I������Ə����܂��D�Ԉ���Ă���Ώ����܂���D�v�ɏ]���āC���Ɠ���I�ׂC�̓_���ʂƓr���o�߂Ȃǂ��o�܂����C���Ă��邾���ł́C�r���o�߂͏o�܂���.���a�ł��Ȃ������ł�����܂���D���ɖ��Ɠ���������Ă��鎞��͐̂̂��Ƃł�.�R���s���[�^�ɍ̓_������̂ł��D�������C����C�ԈႤ���Ƃ�����C�����������Ǝv����������܂��C�N�����Ă��܂���D
�@�Ȃ��CiPhone�Ō��Ă���̂ł�����C���̃y�[�W�ł͂Ȃ��C�X�}�z�p�̋��ނ̕�������ׂ��ł��D�i��ʂ̏c���䂪�Ⴂ�܂��j
���m�ʂ̕ł���̎���ɑ���n[2���3��̕����ɂ��ā^20.11.19�n
�|2��3��
�����m��ҁn�F�A�����肪�Ƃ��D(1) ����Ȃ̂��ӌ��Ȃ̂��C���͂ɂ��Č����ׂ��ł��D (2)���̌`�ň��ꓚ�`���Őq�˂�ƁC�����g�ɒ����܂���D�����肪�ς��C�܂��ʂ̎�������Ȃ���Ȃ�Ȃ��Ȃ邩��D��肪�ς���Ă��ł���悤�ɂ��邽�߂ɁC���̃y�[�W�����ɓǂނ悤�ɂȂ��Ă���̂ł��D
�@�����P�C
^3&chf=bg,s,fff9f9)
�ł�

�ł��C���̃y�[�W�̒��Ɏ�|����͏����Ă���܂����C���̂ǂ���Ȃ̂��͏����Ȃ��ƁC����̈Ӗ������܂�܂���D
�@3�����ϊ��~�X����
�o����Ό����܂ŏ����Ē������炠�肪�����ł��I
�����m��ҁn�F�A�����肪�Ƃ��D���̏�ʂŌ����Ƃ������t���̂́C�z��O�ł��D����Ό����܂��D���肦�Ȃ��b�ł�
���m�ʂ̕ł���̎���ɑ���n[�����}�`�ƕӂ̔��ɂ��ā^20.11.14�n
���������A�}�`��傫���`���Ăق����ł��B
�ł��A���e�͑f���炵���ł��B���ɂȂ�܂��B
�����m��ҁn�F�A�����肪�Ƃ��DiPad mini���c�ɂ��Ďg���Ă�����悤�ł����CPC�p�̋��ނł̓h�b�g��������܂���̂�,�X�}�z�p�̋��ނ����Ă��������D
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝�ɂ��ā^20.11.11�n
�y3�ԁz�Ȃ͌ʂ��t�ɂȂ��Ă��Ă�����肾�Ƃ������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���̃O���t�ɂ��ā^20.11.11�n
�ƂĂ�������Ղ������Ŗ�������̂łƂĂ������Ǝv���܂�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Q�_�Ԃ̋����̌����ɂ��ā^20.11.09�n
����������ŕ�����ɂ���
������������ɂ���
�����m��ҁn�F�A�����肪�Ƃ��D���͌����悤�ł��D�P�y�[�W�ɐ}���X������̂ɁC����������łƂͥ��
���m�ʂ̕ł���̎���ɑ���n[�O�����̒藝�̉��p�ɂ��ā^20.11.09�n
�w���ڐ����Ƃ����������𑝂₵�Ă������������ł��I
�����������₷���ď�����܂���‼
�����m��ҁn�F�A�����肪�Ƃ��D����Ȃ�ɖ�萔�͑�����������ł�������ʂ̊ϓ_���猾���C���C���N�������Ƃ������Ƃ炵���̂ŁC�悩����
���m�ʂ̕ł���̎���ɑ���n[����ɂ��ā^20.11.07�n
���������킩��Ȃ��āA������̃T�C�g�������痝���o���āA��肾�������w�����ӂɂȂ�����ł͖����̂ł����A�y�������Ƃ����悤�ɂȂ�܂����I���肪�Ƃ��������܂����I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����̕ό`�i�������j�ɂ��ā^20.11.02�n
��������ɕ�����₷���ȂƎv���܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[����ɂ��ā^20.11.01�n
�ȒP�ł����B�������ڂ�̖l�ł��A�킩��܂����B�l�́A���̍��̃g�b�v�ɂ����܂��B����A���E�̃g�b�v�ɂ����܂��B���ꂩ��A���E���A��A�v�����������܂��B20�N��ɂ́A�l�͌o�c�ҁA�݂Ȃ���́A�J���҂̂悤�ȗ���ɂȂ��Ă��邱�Ƃł��傤�B�������A����ł́A�x�����܂��B�Ȃ̂ő��}�ɁA�l���g�b�v�ɂ��y�������Ƃ��Ă��������B�ł́A�l�͂��̓y�䂪��������Ƃ����y���݂ɑ҂��Ƃ��܂��B
�����m��ҁn�F���v���ȁH���͈̔͂̏�k�Ȃ�@�ɂ͐G��Ȃ��Ǝv���܂������
���m�ʂ̕ł���̎���ɑ���n[�S�����ɂ��ā^20.10.28�n
���肪�Ƃ��������܂��X�S��������₷�������ł��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�A���������̉������i����@�j�ɂ��ā^20.10.28�n
x=�T����7��3x-2�ɑ��������@
�����m��ҁn�F�A�����肪�Ƃ��D�ς�����q�˕��Ȃ̂ŁC�ڂ��_�ɂȂ�D���ʂ́u���̓����s������ǂ��ɍs�������̂��v�Ƃ������ʂ�q�˂�D���Ȃ��̎���́C���̓��͂ǂ���������悢�̂��Ɛq�˂Ă���̂Ɠ����ɂȂ��Ă��܂��D���������@�́H�ƕ����ꂽ��C�u���������悢�v�ƃI�E���Ԃ��ɓ����邵���Ȃ��D
�@���Ԃ�C�u���������ǂ��Ȃ�܂����v�Ɛq�˂�ׂ��Ƃ�����C�q�˕����Ԉ�����Ƃ������Ƃ��ȁD
-2=\frac{21-10}{5}=\frac{11}{5}&chf=bg,s,fff9f9)
�@�����P�C����������������D���̃y�[�W�͘A���������̉������̃y�[�W�Ȃ̂ŁC�S�R�W�̂Ȃ����������͕̂��s���ł��D
���̂悤�Ȍ`���ɂ��Ă邽�߂킩��Ȃ�����������ǂ݂Ȃ���������Ƃ��ł��܂����B�L��������܂��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�P���������̕��͑��ɂ��ā^20.10.25�n
�ǂ����Ԉ���Ă��邩�����ė~�����ł�
�����m��ҁn�F�A�����肪�Ƃ��D�������Ă���̂�����C�ƈႤ�Ƃ��낪�Ԉ���Ă���̂ł͂Ȃ����D���������C�����̓��Ă������Ȃ��ƁC�u�ǂ����Ԉ���Ă��邩�����v�邱�Ƃ͂ł��Ȃ��D�������C���̘f���̏Z���ͥ��
���m�ʂ̕ł���̎���ɑ���n[�s�����̉������ɂ��ā^20.10.25�n
������₷���ď�����܂���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���̂̕\�ʐ�(�~���C�p���C�~���C�p���̕\�ʐ�)�ɂ��ā^20.10.25�n
�����}�`�̗~����
�����m��ҁn�F�A�����肪�Ƃ��D���ё́i�����̕���ӏ��j�Ȃǂ́C�̐ς��\�ʐς���߂��āC�u�߂�����͋y���邪���Ƃ��v�u�قƂ�ǂł��Ȃ����ɂȂ�܂��v�D�P���ɑO����~���̂悤�ɂQ�g�ݍ��킹�������̌`�Ȃ�C�����ΏI��肾����o�肷��Ӗ��͔����D
���m�ʂ̕ł���̎���ɑ���n[�A���������ƃO���t�ɂ��ā^20.10.25�n
�ƂĂ��킩��₷����肾�����O���t�̏��������悭���������B�ƂĂ��ǂ������������Ǝv���B����2�A3��������Ă��ǂ��Ǝv��
�����m��ҁn�F�A�����肪�Ƃ��D�i�ʔ������ϊ��̃~�X�F�����������j��̍����Ȃ̂ŁC���̂����\���
���m�ʂ̕ł���̎���ɑ���n[�P���������̉������ɂ��ā^20.10.24�n
�ʔ��������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����`�̕������ɂ��ā^20.10.24�n
�����ɓ�������͂��Ă݂��Ƃ���A��������悭����듚�Ȃǂ̐������o�Ă��܂����B
���̖��̌듚�Ȃǂ����Ă݂����Ǝv���Ă���ɐ�����͂��Ă݂��Ƃ���ŋC���t���܂����B
�u����A�������͂��������������ɐ������Ă��܂��Ă���̂�������A���w���̐�������悭����듚���������W�v�ł��Ȃ�����Ȃ����B�f�[�^���������Ă��܂����B���߂�Ȃ����v
�����m��ҁn�F�A�����肪�Ƃ��D���݁C�W�v�͂��Ă��܂���
���m�ʂ̕ł���̎���ɑ���n[�A���������̍���������͑��ɂ��ā^20.10.20�n
�F�X�ȃp�^�[���̖�肪�����ĂƂĂ����K�ɂȂ�܂���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������ɒ������K�ɂ��ā^20.10.22�n
4.21���ŕ\����
�����m��ҁn�F���̖��ŁC������q�˂�̂Ȃ�Ƃ������C���܂ŕ����̂́C�����̂��߂ɂȂ�Ȃ��D�Ⴊ�����Ă���̂�����C��������āC�����̖��ɂ��Ă͂߂�̂ł��D

�ł́C4.21�́H
�����͕�������܂��H
�����m��ҁn�F�A�����肪�Ƃ��D�ǂ̖�肩�����Ȃ��Ǝ���ɂȂ��Ă��܂���
���m�ʂ̕ł���̎���ɑ���n[�H�����̔Z�x�ɂ��ā^20.10.18�n
���ӓ_���ڂ���������Ă�����A�����͂ł����肵�āA�e�X�g��o�b�`���ł��I�{���ɂ��肪�Ƃ��������܂�(^^)
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����}�`�ƕӂ̔��ɂ��ā^20.10.15�n
������₷���������ǂނ���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�l���v�Z�̗D�揇���ɂ��ā^20.10.14�n
�ł�8��2�~�i2�{2�j=16�ł����H
�����m��ҁn�F�A�����肪�Ƃ��D���̒ʂ�D�ł�8��2�~�i2�{2�j=4�~(2+2)=4�~4=16
���m�ʂ̕ł���̎���ɑ���n[�P���������̕��͑��ɂ��ā^20.10.11�n
������₷�������ł�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������̕��͑�i�H�����̔Z�x�j�ɂ��ā^20.10.11�n
5%�̐H����300g��10%�̐H����50g�������H����������B���̐H�����ɉ�g�̐����������4%�̐H�����ɂȂ邩�ƌ��������������ĉ�����
�����m��ҁn�F�A�����肪�Ƃ��D
���̃y�[�W�̈�ԉ��ɂ�����������������������D�͂��߂�A�̗��Ɂu5%�̐H����300g��10%�̐H����50g�v���������݁C�o�Ă�������B�̗��ɏ�������.���͓K����100�������肩��n�߂�D���ʂ�4%�����Z���Ƃ��́C���̕��ʂ𑝂₷�D���ۂɂ�2,3��ł��傤��4%�ɂȂ�
�ƂĂ�������₷���ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������̕��͑�i���̗��K�j�ɂ��ā^20.10.10�n
���̍������킩��Ȃ�
�����m��ҁn�F�A�����肪�Ƃ��D���̖��́u�^�������āv�u�w��ł��������v=�܂ȂԂ́C�܂˂Ԃ���n�܂�
���m�ʂ̕ł���̎���ɑ���n[�A���������ƃO���t�ɂ��ā^20.10.06�n
�ƂĂ��킩��₷��������܂������肪�Ƃ��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�A���������̉������i����@�j�ɂ��ā^20.10.05�n
�����Ǝv���܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�m��(���Z�������) �ɂ��ā^20.10.05�n
�ƂĂ��ǂ������ł��B���w3�N�̑���A�e�X�g���I�����Ȋm�����������悤�ƌ������Ă���Ă݂܂����B��{�I�Ȃ��̂ł������ȃp�^�[���ł�邱�Ƃł�������g�ɂ��܂����B���̃p�^�[���Ȃ炱�̎��`�}���Ƃ����ɂ킩��悤�ɂȂ�܂����B������ƂĂ��킩��₷���Ă������ނ��Ǝv���܂����B���p�����������ɏo��悤�Ȃ��̂��Ə��ǂ��Ǝv���܂��B2���Ԕ����炢�őS�ĂƂ��I��肨�����l�ŋ��Ȋm�����������邱�Ƃ��ł��܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������̕��͑��ɂ��ā^20.10.05�n
���K���̓������̂������������Ǝv���܂��I
�����m��ҁn�F�A�����肪�Ƃ��D���͏����Ă���܂��D�������ڂ��Ă��Ȃ��Ƃ����l�́C�̓_�{�^���������Ă��Ȃ��l==�������Ă��邾���̐l�ł��D
���m�ʂ̕ł���̎���ɑ���n[�P�����̕��͑��ɂ��ā^20.10.05�n
1����������Ȃ�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������̍����ɂ��ā^20.10.05�n
�̓_���Ă����̂��ǂ��Ǝv���܂� �É����^��1�j
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����Ɛ����i�������j�ɂ��ā^20.10.04�n
�̂��F�I�ō��ł��I���W���������팸�ł��A���ǎ��Ȗ��I���肪�Ƃ��������܂�(*�L���M*)
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�H�����̔Z�x�ɂ��ā^20.10.03�n
���A���A�S�Ă��ǂ�������܂������m�̃e�X�g�ł���������肪�o��̂Ŋ��ӂ��Ă��d��Ȃ��ł�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�A���������̗��p������͑�1�ɂ��ā^20.10.01�n
���P�̖���Ⴆ�ɂ���ƁA�q���1��210�~�A�݂���P��80�~�͖��ɓK���Ă���B�r�Ƃ������͂���ꂽ���������Ǝv���܂��B�A�����������g�������Ȃ̂ł��̕��������̂ł͂Ȃ��ł��傤���B
�l�͊w�Z�Ő搶�ɂ��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D�搶�̋������ɍ��킹��Ƃ悢�ł��傤�D
�@�������C�茳�ɂ��钆�w2�N���w�̋��ȏ�15���̂����ŁC���̗�����͂����肳���Ă���̂�4���ŁC�c��͂����ł͂���܂���D��ʂɁC��w�����ł�1���̋��ȏ��ł����グ�Ă�����e�͏o��ł��܂����C���Z�����ł́C���ׂĂ̋��ȏ��ɋ��ʂ��Ă�����e�����o���Ȃ��i���Ȃ��Ƃ������ł́j�Ƃ����̂��Öق̗����ł��傤�D������C���_�͂�������ǂݎ���Ă��������D
�@���ɁC�A���������Ɍ��炸�C�r���̕ό`���������������Ȃ�ꍇ�C��ʂɂ́u�K�v�����v��ǂ��ĉ����߂铚�ĂɂȂ�̂ŁC�\�������̌������K�v�ɂȂ�܂��D������C�u���̓��͖��ɓK���Ă���v�Ƃ����\�����̊m�F����������悢���ƂɂȂ�܂��D�Ƃ��낪�C���w���ɂ́C�K�v�����C�\�������Ƃ����T�O���p��������Ȃ��̂ŁC�u���̓��͖��ɓK���Ă���v�ƌ����Ă��Ӗ��̂�����̂Ƃ͂Ȃ炸�u�����ɂ̓n���R�������Ă����悤���悢�v�Ƃ����̂Ɠ��l�̌`���I�Ȗ��ɋ߂���舵���ɗ����\�����傫���ł��D
�@�����ƊȒP�ȕ������C�Ⴆ��
2x=6�������āC
x=3�Ə������ꍇ�ł��C���̏������ł�
x=3�͒P�Ȃ�K�v�����Ɠǂނ��Ƃ��ł���̂�,�u
x=3�͌��̖��ɓK���Ă���v�ƌ����ꕶ���K�v���ƌ����o���C���ׂĂ̖��ɊY�����邱�ƂɂȂ�܂��D�������C���w���Z�ň����C�ȒP�ȕ������̕ό`�́C�قƂ�ǂ̏ꍇ�C���l�ό`�ɂȂ��Ă��āC���ł��t�����ɂ��ǂ����̂���Ȃ̂ŁC���̂����܂�̕��͂͏ȗ��ł��邱�ƂɂȂ�܂��D
�@���l�ό`�������悤�Ȃ��̂Ƃ����C���ӂ��Q�悷��ꍇ�̂悤�Ɍ��ɖ߂�Ȃ��ό`���܂܂��ꍇ�ł��D�Ⴆ�C

�ł͉E�����ɕό`���Ă����ƁC���ɂ͖߂�܂���i

�͓����Ɋ܂܂�Ȃ�����j
�@�Ƃ��낪�C���w�Z�ň����A���������́C1���������̑g�Ȃ̂ŁC2�悵�ĕό`����悤�ȓ��l�W�������ό`�͓o�ꂹ���C��ɋt�ɖ߂��悤�ɂȂ��Ă��܂��D������C�\�����̌����͏ȗ��ł���̂ł��D
�@���X�Ə����܂������C�u���ɓK���Ă���v�Ƃ����n���R�ʼn����悤�ȍ�Ƃ��o����̂łȂ��C���ۂɁu���Z�v������Č��Č��̖�肪���藧���ǂ������ׂ�K����g�ɒ���������d�v�ł��D�N�ł��v�Z�ԈႢ�͂���̂Łu���Z�v���Ċm���߂�̂ł��D�\�����̌����ƌ����p��͒��w�ł͏K���܂��C���Z�͏��w���ł������錾�t�ŁC���ꂪ�\�����̊m�F�ɑΉ����Ă��܂��D�i���Ɂu���Z���܂����v�ȂǂƏ����K�v�͂Ȃ��j
�Q�l�ɂȂ�܂����I���肪�Ƃ��������܂����B
�킩��₷�������ł��I
�撣���Ă��������B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�A���������̉������i����@�j�ɂ��ā^20.09.26�n
72x+72y=80x+65y
80x=65y+400
�Ƃ����v�Z���������̂ł����o���Ȃ��̂łł���悤�ɂ��ė~�����ł�
�����m��ҁn�F�A�����肪�Ƃ��D1���C���ɊȒP�ɂ��Ă����悢�D
72x+72y=80x+65y��8x=7y�D
������Q�ڂ̎��ɑ���D
70y=65y+400
5y=400
y=80
8x=7y�ɑ��
x=70
�y���2.2�z���a��9cm�@3cm�ɒ������肢���܂�
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝�ɂ��ā^20.09.24�n
���₷���ĕ�����₷�������ł��I�I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������ɒ������K�ɂ��ā^20.09.23�n
14���ɒ����ƁH
�����m��ҁn�F�A�����肪�Ƃ��D���w�Z5�N���ȏ�ł��̎��₪���邱�Ƃɂ��ẮC�[���ł��܂��C�ꉞ�Ԏ��������Ă����܂��D

�ƂĂ�������₷�������ł��B
�����ɏo����悤�ɂȂ�܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~�ɓ��ڂ���l�p�`�ɂ��ā^20.09.09�n
�w���̍��̕��K�Ɏg�킹�Ă�����Ă��܂��B���肪�Ƃ��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������̕\�����ɂ��ā^20.09.08�n
�Ō�̖��́A������A���������łȂ��A�r�����������ĉ�����ĖႦ�܂����H
�����m��ҁn�F�A�����肪�Ƃ��D������A���������łȂ��A�r�����������ĉ�����Ă���̂ɁC�u������A���������łȂ��A�r�����������ĉ�����ĖႦ�܂����H�v�Ƃ́H
���m�ʂ̕ł���̎���ɑ���n[�ω��̊����ɂ��ā^20.08.29�n
�ꎟ��y=3����2x+5��
x�̑����ʂ�1�̂Ƃ�
x�̑����ʂ�3�̂Ƃ�
y�̑����ʂ����߂Ȃ����Ƃ������ŋ����Ă��������܂����H
�����m��ҁn�F�A�����肪�Ƃ��D��肪�Q�菑���Ă���Ƃ������Ƃł�����C���߂̖�肪2/3�C���̖�肪2�ł�
���m�ʂ̕ł���̎���ɑ���n[�����̐����ɂ��ā^20.08.27�n
�ƂĂ�������₷������
���肪�Ƃ��������܂�(*^^*)
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�s�����̎g�����ɂ��ā^20.08.27�n
�ƂĂ�������₷�������Ɩ������肪�Ƃ��������܂���( �E�́E)�m
�����m��ҁn�F�A�����肪�Ƃ��D
��??�m??�^20.08.25�n
���̃T�C�g��q�������Ă��������܂����i���傤�Ǒ����e�X�g�̑O�j�B���n�����Ȏ��ł��悭�������邱�Ƃ��ł��܂����B
������q�������Ă������������v���܂��̂ŁA�ǂ����A�킩��₷���������낵�����肢�������܂��B
������撣���Ă��������I�I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���̐��E���̐��ɂ��ā^20.08.25�n
��葝�₵�Ă�������
�����m��ҁn�F�A�����肪�Ƃ��D���̃y�[�W�i��ł�������
�����{�m������S������^20.08.23�n
���Ղ��ĕ�����₷�������B���肪�Ƃ��������܂��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������ɒ������K�ɂ��ā^20.08.23�n
�V�l�̎��ł��A�킩��₷������������B�悩�����ł��B�L��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�ω��̊����ɂ��ā^20.08.22�n
�����ʂ������ė~���� �����ʂ̋��ߕ�
�����m��ҁn�F�A�����肪�Ƃ��D��ԏ��߂ɏ����Ă����ˁD������g���āC�����������Ⴊ������Ă����ˁD
���m�ʂ̕ł���̎���ɑ���n[�P���������̕��͑��ɂ��ā^20.08.21�n
��x���߂�ƕʂ̖��ɂȂ��Ă��ē�����肪�o�Ă��Ȃ�����
�����m��ҁn�F�A�����肪�Ƃ��D����ǂ�ł��������Ɠ����������������ɏo�Ă���̂��C�]�����炠�镁�ʂ̖��ŁC�����o���Ă��܂��̂ŗ��K���ʂ������Ȃ�D����ɑ��āC����C���Ɖ��ς��̂��C���ʏ㓙�̖��ł��D
���m�ʂ̕ł���̎���ɑ���n[�����̕ό`�i�������j�ɂ��ā^20.08.18�n
�ƂĂ����ɗ����܂��� ���肪�Ƃ��������܂�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�A���������̍���������͑��ɂ��ā^20.08.17�n
�e�X�g�ɏo�����Ȗ�肪�����ď�����܂����I�I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���̒��ɂ��ā^20.08.17�n
�ƂĂ��ڂ����������Ă���āA���w���ɂ��킩��₷�������B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������ɒ������K�i���w�����j�ɂ��ā^20.08.16�n
0.894069671630859375
�����m��ҁn�F�A�����肪�Ƃ��D���̃y�[�W�͒��w�����̋��ނł����C����҂͒��w���ł��C���Z���ł��Ȃ��C���w�Z�̊w�����Љ�l�ł��傤�D���̂��炢�̔N��ɂȂ�C������Ȃ��̂ŋ����Ă��������ƌ��t�ŏ����ׂ��ł��D�v���O��������̌P���p�ɏo�肳�ꂽ���Ȃ�C���[�v��ċA���g���āC�T����������Ă��邩���邱�ƂɂȂ�ł��傤.���ʂ͕�����܂����C����̏�����������ł��̂ŁC���͋����܂���D
���m�ʂ̕ł���̎���ɑ���n[1�����ɂ��ā^20.08.16�n
Next�ł͂Ȃ��Ď��̖��Ƃ���ƕ�����₷���Ǝv���܂����B
����ȊO�͉���₷�����g���₷���Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ�.�u�~�܂�v�����ł͕�����ɂ����̂ŁuSTOP�v�Ə�������ɂȂ����悤����
��??�m���O�Ȃǖ����^20.08.12�n
��������͂���ۂɁ|��ł��Ă�✖�ɂȂ�
�����m��ҁn�F����y�[�W�����ނ�����̂ɁC�ǂ̃y�[�W�̘b�Ȃ̂��������Ȃ��ƁC���̘b���ʂ��܂���D
���m�ʂ̕ł���̎���ɑ���n[�A���������̍���������͑��ɂ��ā^20.08.12�n
�����������肪�Ƃ��������܂��I
�����m��ҁn�F�A�����肪�Ƃ�
���m�ʂ̕ł���̎���ɑ���n[�O�p�`�̖ʐ��ɂ��ā^20.08.11�n
��3�̎q�ǂ��̋��ȎO�p�`�̒�ӂƔ�̖̂ʐς̖�肪��{�̉�@������܂ŋ������Ă���A��ς킩��₷���A������܂����B���Ӑ\���グ�܂��B
�����m��ҁn�F�A�����肪�Ƃ�
���m�ʂ̕ł���̎���ɑ���n[�������ɒ������K�ɂ��ā^20.08.05�n
���������ɂȂ镪���������Əڂ��������ė~�����ł�
�����m��ҁn�F�A�����肪�Ƃ��D���̃y�[�W�̋��ނ́u���w�����v�Ə����Ă��܂��悤�ɁC���w�����璆�w�P�N�����ǂނ��Ƃ�z�肵�����̂ł��D������,
���������̏ڂ�������͍��Z�R�N���ŏK���������䋉���̘a�Ƃ������ڂɂ���܂��D���Ԃ�C��߂��ēǂނ͖̂����ł��D
�Q�l�ɂ����Ă�������
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Q���������̓������ �ɂ��ā^20.08.04�n
�ƂĂ��悩�����ł��B�������������Ђ������ۂ������~���������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������ɒ������K�ɂ��ā^20.08.04�n
���ɁA������₷�������ł��B��A�Ō�̕��ɖ����o���Ă����̂��A�悩�����ł��B�������A���ɂȂ�܂���(�@�O�́O)
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�A���������i���Z�������j�ɂ��ā^20.08.04�n
���������ɂ����B���₷�����āB
�����m��ҁn�F�A�����肪�Ƃ��D��������MicroSoft�Ђ��C�u����Internet Explorer���g���̂͂�߂悤��v�ƌ����Ă���̂ɁC�����Ďg���Ă���l�̍l�����������ł��܂���D
�H�m�`�b�`����^20.08.01�n
���͍ŋ߁A���w�Z�őf�����������K���܂����I����ŁA���Ƃŗ����͏o�����̂ł����A���K���������Ȃ��Ǝv���A�g�킹�Ē����܂���✨�Ȃ��Ȃ����T�C�g�����Ă��A�ǂ���肪�����炸�A�����Ă�����ł��B�B�B�ł��A���̃T�C�g�������āA���������Ă݂āA�������ǂ��ȂƎv���܂����I�I�p�\�R���łƃX�}�z�ł�����̂��g���₷���ėǂ������ł��B�i������O�̎��Ȃ̂��ȁc?�j����ɁA������ׂ����L�ڂ���Ă���̂��A������������₷���A�𗧂����Ē����܂����I�����ė~�����Ƃ���́A���I�ɂ͂���܂���B�喞���ł�(*�L�ցM*)�܂��A�e�X�g�O�Ɏg�킹�Ē��������Ǝv���܂��I���肪�Ƃ��������܂����I���ꂩ����A�撣���ĉ�������☺️fighting!!
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������ɒ������K�ɂ��ā^20.08.01�n
�킩��₷�������ł���❣
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[��@�̌����ɂ��ā^20.08.01�n
��l�ɂȂ�A�o�ς̕������邽�߂Ɍo�ϐ��w�̖{���w�������̂ł����A���Z�̐��w���o���ĂȂ��Ǝv��������̃T�C�g�ō��Z�̐��w���͂��߂���A��������������Y��Ă��肱����̃y�[�W�͂ƂĂ��ǂ����K�ɂȂ�܂����B���K��肪���邱�ƂŁA�������[�܂�܂��ˁI
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�A���������̕��͑�2�ɂ��ā^20.07.29�n
�����A�w�Z�ɏo������Ǝ��Ă��Ă킩��₷�������ł��I�I�܂��A���������łȂ��A���̍�����������܂Ő��������������߁A��葁�������ł��āA�e�X�g�O�̕��K���Ƀs�b�^���ł��I�{���ɏ�����܂����A���肪�Ƃ��������܂��I�I�I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����i�S����,����,�����j�ɂ��ā^20.07.28�n
���X�����肾�������������x����Ă݂����ł�
�����m��ҁn�F�A�����肪�Ƃ��D�i���{���̖��O�͌��J���Ȃ������悢�D�y���l�[�����炢�ɂ��ĉ������j
���m�ʂ̕ł���̎���ɑ���n[�����v�Z�̓�������ɂ��ā^20.07.27�n
����e�X�g��Ƃ��Ďg�킹�Ă���������A�ƂĂ��悭�ł��Ă���I���ꂪ�����Ƃ́A�Ȃ�Ă��炵�����̒��Ȃ̂��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�P���������̕��͑��ɂ��ā^20.07.25�n
���̒������c�̒�����2�{���3�Z���`�Z�������`������B���̒����`�̂܂킵�̒�����30�Z���`�ł���Ƃ��A�ꌳ�ꎟ��������p���āA�c�A���̒��������߂Ȃ����B
�����m��ҁn�F���̂܂ܓǂ߂C���l�̂��肩�ȂƂ������͂ɂȂ��Ă���ˁD���̂܂ܓ�����ƈꐶ���Ⴂ���ĕ�炷��������Ȃ��̂ŁC�����܂���D������Ȃ����Ƃ�l�ɐq�˂����Ƃ��́C������Ȃ��̂ŋ����Ă��������Ƃ����ׂ��ł��D���łɁC�܂킵�͂ǂ������܂�����
���m�ʂ̕ł���̎���ɑ���n[�P�����̃O���t(�X��)�ɂ��ā^20.07.22�n
�C�j�X���̕��������̂Ƃ�
�Ⴆ�̂Ƃ��C-2/3�u�E��2�i��ł���C����2�i�ށv
�@-1���ȁH
�����m��ҁn�F�A�����肪�Ƃ��D�����̕��@�͈Ⴂ�܂����C�������܂���
���m�ʂ̕ł���̎���ɑ���n[�������������ƂȂ邎�̒l�ɂ��ā^20.07.18�n
��m�Q��{�Ȃ@�̐�����������ɂ���
�����m��ҁn�F�A�����肪�Ƃ��D���w���ɂ͓���ꍇ������D����ȏ�͌����邱�Ƃ��Ȃ��D
���m�ʂ̕ł���̎���ɑ���n[�������ɒ������K�ɂ��ā^20.07.13�n
0�A833�c�́A�����ŁH
�����m��ҁn�F

��͎�����..�D
�̓_�@�\�����Ă��ĂƂĂ����₷�������ł��B���肪�Ƃ��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������ɂ������ɂ��ā^20.07.08�n
������₷���ł�
���肪�Ƃ��������܂���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���̐��E���̐��ɂ��ā^20.07.05�n
�ǂ����́A�Q�[�����o�Ŗ�肪�����邱�Ƃł��B
�������́A��萔�����Ȃ��������Ƃł��B
����ۂł��Ă���Ε���Ȃ��ł��B
�����m��ҁn�F�A�����肪�Ƃ��D��肪�����ďo�肵�Ă���̂ŁC�����̃T�C�h���j���[���玟�̃y�[�W�ɐi�߂悢
���m�ʂ̕ł���̎���ɑ���n[���ɂ��ؖ��ɂ��ā^20.07.04�n
��������Ȃ������I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�A���������̕��͑��ɂ��ā^20.06.26�n
���̎�ނ��L�x
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������ɒ������K�ɂ��ā^20.06.27�n
0��0�����ɂ����0/0�Ł@���q���ꂪ�����ł��邩��@1�@�ɂ͂Ȃ�Ȃ��̂ł��������Ă�������
77�Βs��V�l
�����m��ҁn�F�A�����肪�Ƃ��D���w�P�N���̂S���̏��߂ɏK���͂��̉ӏ��ł����C�u�O�Ŋ��鏜�@�͍l���Ȃ��v�Ƃ����`�ňꌾ�ōς܂��Ă��܂����Ƃ������C�����ɓ��ݍ���ōs���Ă��قƂ�lj��������Ȃ��ƌ����o�����l�܂����m�b��������Ȃ��D
�@�������ݍ����ȏ�(A)�ł́C�u����Z�v���u�t���̊|���Z�v�Ƃ��Ē�`���C����ɂ���āu�O�Ŋ��銄��Z�͍l���Ȃ��v���Ƃ������Ă��܂��D
���Ȃ킿�C�ǂ�Ȑ�

�����������C

�ɂȂ�C

�ƂȂ邱�Ƃ͂Ȃ�����C0�̋t��

�͑��݂��Ȃ��D����ɂ��C�������鐔

���O�Ŋ���v�Z�́C

��0�̋t�����|���邱�Ƃɂ���Ē�`����邩��C�i

�j0�̋t������`�ł��Ȃ��ȏ�C�O�Ŋ���v�Z�͒�`�ł��Ȃ��D
�@���������C��̓I�ɏ����Ă��鋳�ȏ�(B)�ł́C�O���P�C�O���Q�C�O���R����ƂO���O���ď����Ă���D
���Ȃ킿�C�ǂ�Ȑ�

�����������C

�ɂȂ�C
&chf=bg,s,fff9f9)
�ƂȂ邱�Ƃ͂Ȃ�����C
&chf=bg,s,fff9f9)
�Ƃ����v�Z�͒�`�ł��Ȃ��D
�@���ɁC

������C

�Ƃ����

�Ƃ��Ă��邱�ƂɂȂ薵���C

�Ƃ����

�Ƃ��Ă��邱�ƂɂȂ薵���C����ǂ����߂Ă����̒l�ƏՓ˂��邩�疵���D���ǁC�l�����߂��疵�����N����D
�ƂĂ��A����Ȃǂ������Ă��肢���ȂƎv���܂����I�I������ƂĂ�������₷�������ł��I�I����@�̐F�X�̖�肪�������̂Ńe�X�g���ɂ����ȂƎv���܂����I�I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������̘a���ɂ��ā^20.06.23�n
�u�}�C�i�X�v���u�i�C�}�X�v�ɂȂ��Ă��܂��B
�y����z
�@���̗�̂悤�Ɂu�������v������Ƃ��́C�͂��߂Ɂu�������v���O���܂��D
�@���̏ꍇ�C�������}�C�i�X�̂Ƃ��̓i�C�}�X�̕������Ɗ|���܂��D
�����m��ҁn�F�A�����肪�Ƃ��D�U�M�g���Ƃ��A�{�J�h�ȂǃJ�^�J�i4�����̂��͎̂苭���I�������܂���
���m�ʂ̕ł���̎���ɑ���n[�A���������̉������i����@�j�ɂ��ā^20.06.22�n
�ƂĂ��킩��₷���ł�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���̕ψ��ɂ��ā^20.06.21�n
�����Ă��Ă������y���������ł��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�_�Ώ̂Ȑ}�`�ɂ��ā^20.06.20�n
�ƂĂ��ǂ������ł� �e�X�g���ɂȂ�܂���‼
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���ލ����܂Ƃ߂��ɂ��ā^20.06.19�n
�������ɗ��B�����Ǝv���B�撣���ĉ������B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���Ώ̂Ȑ}�`�ɂ��ā^20.06.17�n
�ƂĂ��ǂ��A������₷�������B
���̉���܂ł���ƂĂ��ǂ��Ǝv���܂��B🤔
�����m��ҁn�F�A�����肪�Ƃ��D�q���g���N���b�N
���m�ʂ̕ł���̎���ɑ���n[�P�����Ƒ������ɂ��ā^20.06.17�n
�Ƃ��Ă��킩��₷���ł��B
���w�i�Z���j��S������Ă��Ȃ������̂ŁA������Ŋw�тȂ������Ă��������Ă���܂��B
���ꂩ�����낵�����肢�������܂��B
���e�Ɋւ��Ă͊��S�ɖ������Ă���܂��B
���t���K�ؒ��J�ŁA���o���̈��������ł��A�����ł��܂��B
�����A�ł���T�C�g�̐F����ς��Ăق����B
���Ɖ��F�ƒW���s���N�̑g�ݍ��킹�́A������Ǝ�������C�����܂��i���݂܂���j
����������������K���ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������ɒ������K�ɂ��ā^20.06.15�n
���̉�������Ă����Ɗ������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D��ʂɁu�I�������N���b�N����C�̓_���ʂƉ�����o�܂��D�N���b�N���Ȃ���Ή͏o�܂���D�v�Ə����Ă����ˁD�N���b�N���Ă��Ȃ��̂ł����D�����P�C���Ȃ������Ă���̂�PC�p�̃y�[�W�ł��D�X�}�z�p�Ƃ͌��������Ⴂ�܂��D���̂��Ƃ̓y�[�W�̐擪�ɏ����Ă���܂��D
���m�ʂ̕ł���̎���ɑ���n[�P�����Ƒ������ɂ��ā^20.06.14�n
������₷�������ł��B
�����A�����^��Ɏv�����̂ł����Aa��������a�~1�ŁA������1�ƂȂ�̂��ȁA�Ǝv�����̂ł����������������ė~�����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D����x�ɂ��Ĉ����Ă���̂ŁCa,b,y,...�Ƒ��̕����S�������グ��K�v�͂Ȃ��ł��傤�D�Ƃ������C����Ȃ��Ƃ��������萔�������Ȃ�߂��āC���C���Ȃ��Ȃ�ł��傤
���m�ʂ̕ł���̎���ɑ���n[�������̕��͑�i���̗��K�j�ɂ��ā^20.06.11�n
�������������Ă��Ă��o�c�ɂȂ�
�����m��ҁn�F�u���p�p�����œ�������̂Ƃ��C���� x �͏������Ƃ��܂��v�Ə����Ă�����
���m�ʂ̕ł���̎���ɑ���n[�����̑召��r�ɂ��ā^20.06.10�n
�����̕t���ĂȂ������ƁA�����̂��������������ɏo�Ă��܂����I���̏ꍇ�͂ǂ���������̂ł��傤���H
9/2�A��a �A��23����̑傫����
(9/2�͕���)
�����m��ҁn�F���̉�������[�Ə����Ă���̂ɁC���̏ꍇ�͂ǂ���������̂ł��傤���H�Ƃ͉������Ă���̂ł����H

2���������̉��̌���x=�|b�}��b2�|4ac2a�𗘗p���āC2�������� x2+x�|1=0�������ƁCx=�|1�}��k2�ł���B���̂Ƃ��Ck=�y�@2�@�z�ł���B
�����m��ҁn�F���̃y�[�W�̉��ɉ������߂�v���O����������܂��̂ŁC�����ɖ����������߂Γ������o�܂�
���m�ʂ̕ł���̎���ɑ���n[��Βl�ɂ��ā^20.06.10�n
�R�̐�Βl������
�����m��ҁn�F���ނ�ǂ�ł��玿�₵�Ă�������
���H�m�c��u�]����^20.06.08�n
���K�ɂ҂�����Ȗ�肪�����ď�����܂��B�~�������Γ�֍��Z�̖���Ƃ����`�Ōf�ڂ��ꂢ��������Ƃ��肪�����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�����肪�ł���͈̂̂����Ƃ��ƍl����̂́C�ł��Ȃ��l�̃R���v���b�N�X���Ǝv���D
�@�Ⴆ�C���l�Z�C�ߋT�Z�C�ߕs���Z����ȂǏ��w�Z�Z���̓���ȉ�������S���o���Ȃ��ƗL�����w�Z�ɍ��i�ł��Ȃ��Ƃ��Ă��C���̂悤�Ȍv�Z�͒��w�Z�Łu�������v���K�����炷�ׂĉ�����悤�ɂȂ邱�Ƃ��番����悤�ɁC���Z�œ��Ɍ�������ł����Z�̎��Ƃŕ��ʂɏK�����𒆊w���ɂ�点�Ă��邾���Ƃ����悤�ȏꍇ�C�����������悤�ɂ��邽�߂ɒ��w�Z�R�N���̑����Ȏ��Ԃ��₷�邱�Ƃ͓�x��ԂɂȂ�C���܂肨���߂ł��Ȃ��D�����ƒ��w�Z�̊Ԃɐg�ɒ����Ă����ׂ�����������͂��ł��D
�@�v��ƁC�M�҂͂��Ȃ��ƍl�������Ⴄ�̂ŁC�����肪�ł��邱�Ƃ��̂����Ƃ��Ƃ͍l���Ă��Ȃ��̂ł��D���ʂ̒��w�������ʂɂł��钆�w�������Z�ɗ��Ăق����Ƃ����l���ł��̋��ނ�������̂ł��D
���m�ʂ̕ł���̎���ɑ���n[�����̐����ɂ��ā^20.06.07�n
�l���S�̓I�ɕ�����Ȃ������̂ŁA�����������ƂĂ��������[�܂�܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�_�Ώ̂Ȑ}�`�ɂ��ā^20.06.07�n
�킩��₷������łƂĂ��[���o���܂����I������g���Ă���̂ł����A��͂�g���₷���ł��I����Ƃ��g�킹�Ă������������ł��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[ �~���p�̒藝(�������)�ɂ��ā^20.06.06�n
�悭�܂Ƃ܂��Ă܂��B�~���p�̖��͈ӊO�Ɠ��
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�f���ɂ��ā^20.06.05�n
�f�����w���D�x�ł̑n���ߒ��Ŋς鎩�R���̊G�{
�m�������̂��ɂ̂����Ȃ��[��
�ߘa2�N�T��23���`�U���V���@�̊Ԃ���
�ː��s�哇�G�{�ق�
�w�g�g�m�h���]�x�Ŋς鎩�R���̊G�{����B
�L�c�쒬�d�q���Ёu����͂̂邬�v
��u�]�����肢�v���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�c���݂���͖��N�_���{�[�����Ƃ��������̂ŁC�݂���̔�]�Ȃ�ł��܂����C���̐l�̏������{�̔�]�͂��܂���D
���m�ʂ̕ł���̎���ɑ���n[�����i�S����,����,�����j�ɂ��ā^20.06.02�n
�킩��₷���Ă߂�������킩��I
����ŕ��K�o�b�`���ł��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����̕ό`�ɂ��ā^20.06.02�n
���ۂɖ��������ĉ���͂��鏊������̂ł����A�A���t�@�x�b�g�̑啶����S�œ��͂����Ƃ���ANo�Əo�Ă��܂����̂ŁA�������őł�OK�Əo�܂����B���ׂȎ��ł��������������łȂ��A�啶���ł�OK�Əo��悤�ɉ��P���鎖�͏o���܂��H�ق�̍��ׂȎ��ňӌ����Ă��܂��܂������A��낵�����肢���܂�
�����m��ҁn�F�A�����肪�Ƃ��D�啶���ł����i�ɂ��邱�Ƃ͂ł��܂����C����͊ԈႢ�Ȃ̂ł���Ȃ��Ƃ����Ă͂����܂���D�啶���Ə������ł͕\���Ă�����̂��Ⴄ�̂����ʂŁC�u���p�������œ��͂��Ȃ����v�Ə����Ă���܂�����C�l���̗]�n�͂���܂���D�i�Ȃ��S�p�����m2�o�C�g�����n�œ��͂��ꍇ�C�i�X�}�z�̋@��ɂ���Ă͔��p�����ɂ��ɂ����ꍇ������炵���j���p�����ɒ����č̓_���鏈���͂��Ă���܂��j
���m�ʂ̕ł���̎���ɑ���n[�����̉��p.�Ă��̌����ɂ��ā^20.06.02�n
�킩��₷��
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���Ώ̂Ȑ}�`�ɂ��ā^20.05.31�n
�킩��Ȃ�
�ŏ��́A�킩��Ȃ������B
�ł��A�킩�����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������ɒ������K�ɂ��ā^20.05.31�n
(3)(6)�̖��̂������ł��܂���B����₷��������肢���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D����ȏ�͖����ł�
����t���mmairu nono����^20.05.30�n
���ȏ��ł͂킩��Ȃ����Ƃ����̃T�C�g�ɋ����Ē����܂����B�ƂĂ��킩��₷�������ł��B�����Ƃ�������̃��p�g���[���L���Ăق����ȂƎv���܂��B���肪�Ƃ��������܂����B�������Ă܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�_�Ώ̂Ȑ}�`�ɂ��ā^20.05.29�n
�킩��Ȃ��������������̂ŕ��ɂȂ���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���ލ��ɂ��ā^20.05.28�n
(5)�̉�����Ⴄ
�����m��ҁn�F�A�����肪�Ƃ��D�r����x�̌W����������܂���
��?[����܂����[����^20.05.27�n
2-(m-n)^2�̈��������̎d���������Ă������������ł��B
�����m��ҁn�F�������̒��ʼn��x�����O��ς���̂́C�^�ʖڂȎ���ɂ͌����܂���D���ɁC2-(m-n)^2�̈��������Ƃ����̂����w���̎��₾�Ƃ�����C���̎ʂ��ԈႢ�ł��傤�D���w���ɂ͂��̂悤�Ȗ��͏o���܂���D���Z�����������͈̔͂ň�����������ꍇ�́C
^2=(\sqrt{2}%2B m-n)(\sqrt{2}-m%2B n)&chf=bg,s,fff9f9)
���̃z�[���y�[�W�ɂ͂Ȃ��̂ł����A8x^2-50y^2�̉������������Ă���������Ə�����܂��B�ł���������ł��肢���܂��B��낵�����肢���܂��B
�����m��ҁn�F���l�ɗ��ނƂ��ɏ���Ɋ���������肷��͎̂���Ȃ��Ƃł�����C�Ȍ�C��t����悤�ɂ��܂��傤�D���ɁC8x^2-50y^2�̉������Ƃ������̂͂���܂���D8x^2-50y^2�͖��ł͂Ȃ�����ł��D�����Ƃ͂����茾���C8x^2-50y^2�͕������Ȃ̂ŁC����������W�J�Ƃ�����肪����܂��D8x^2-50y^2�̈��������̎d���������Ă��������Ƃ������Ƃł�����C
=2(2x-5y)(2x%2B 5y)&chf=bg,s,fff9f9)
4a+5b�|6c+7a�|8c
�����m��ҁn�F���ꂪ�ǂ����܂������H���₪����Ό��t�Ō���Ȃ���Βʂ��܂���
���m�ʂ̕ł���̎���ɑ���n[�P�����Ƒ������ɂ��ā^20.05.25�n
���̋x�݂Ŏ��Ƃ���ꂸ�A�����ƕ�����Ȃ������̂ł����A��������Ă���Ɨ����ł��܂����I
���ȏ����Ɓu�Ȃ������Ȃ�̂��v�ȒP�Ȑ���������̂ɓ�����ɂ͐������Ȃɂ��Ȃ���...�B
�܂��A������Ȃ����Ƃ��������猩�����Ă��������܂��I
�����ƕs���������̂łƂ����Ă�������܂����B���肪�Ƃ��������܂��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���̒l�ɂ��ā^20.05.24�n
x=15�̂Ƃ��A(x+2)2��-(x+1)(x-1)�̒l�̂��Ăߕ��������Ă��������I
�����m��ҁn�F�A�����肪�Ƃ��D��������狁�܂�܂����C�u�����ȒP�ɂ��Ă���������v���Ƃ���K���邽�߂̖�肾�ƍl����Ƃ悢�ł��傤�D
^2-(x%2B 1)(x-1)=x^2%2B 4x%2B 4-(x^2-1)=4x%2B 5=65&chf=bg,s,fff9f9)
��Βl��5���傫���ꌅ�̐����͑S���ʼn��H
�����m��ҁn�F�A�����肪�Ƃ��D�ꌅ�̐����ɕ��̐������邩�ǂ����ɂ���ĕς��܂��D���̐������Ȃ�,6,7,8,9��4�ł�…��������₷��l���Ă���̂��H���̐������ꂽ��,±6, ±7, ±8, ±9��8�ł��D
���m�ʂ̕ł���̎���ɑ���n[�����̕ό`�ɂ��ā^20.05.22�n
�ƂĂ��A������₷�������ł��B�������A�����Ɩ��𑝂₵�������ǂ��Ǝv���܂��B���肪�Ƃ��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����`�̕������ɂ��ā^20.05.21�n
�ƂĂ�������₷�������ł��B��������������Ȃ��������ɖ��ɂ����܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����i�S����,����,�����j�ɂ��ā^20.05.19�n
�킩��₷�������Ă����āA���₷���������A�킩��₷�������ł�‼
���肪�Ƃ��������܂���😊
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�_�Ώ̂Ȑ}�`�ɂ��ā^20.05.19�n
���𗦂���������ǂ��ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D�����Ă�����������܂���…??
���m�ʂ̕ł���̎���ɑ���n[�_�Ώ̂Ȑ}�`�ɂ��ā^20.05.18�n
�ǂ����͕�����₷���ȒP�ɂ܂Ƃ߂��āA�F��ς��Ă���Ƃ���B
�������͂Ȃ����Ȃ��c�B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�_�Ώ̂Ȑ}�`�ɂ��ā^20.05.17�n
������₷���A����~�ɂȂ��Ă���̂͂悢�Ǝv���܂�!
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���̂̕\�ʐ�.�W�J�}�ɂ��ā^20.05.16�n
��3.2�̉���ɂāuAC=��20=2��10�v�ƂȂ��Ă��܂����A�������́uAC=��20=2��5�v�ł͂Ȃ��ł��傤���B
���Ⴂ���Ă�����\����܂���B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[���̂̑̐ρi�������j�ɂ��ā^20.05.16�n
���5.2�̉���Łu�����̂Ƃ��C���炩�Ɂ�OAP�Ɓ�OAQ�͑����}�`�v�Ƃ���̂ł����A��OAQ�̂Ƃ���́�OEQ�̊ԈႢ�ł͂Ȃ��ł��傤���B���̊��Ⴂ�ł�����\����܂���B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[���Ώ̂Ȑ}�`�ɂ��ā^20.05.16�n
���肪�Ƃ�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���Ώ̂Ȑ}�`�ɂ��ā^20.05.16�n
���ɂȂ�܂����B�{�^���Ŗ�肪�����邩����₷�������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���Ώ̂Ȑ}�`�ɂ��ā^20.05.16�n
�_�Ώ̂Ɛ��Ώ̂̐}�`�̍����ڂ��Ă��������B
�����m��ҁn�F�A�����肪�Ƃ��D�܂����ȏ��I�ɂ́C�Ώ̂Ɠ_�Ώ̂ł��̂ł�낵���D���ɁC�����̍��Ƃ͌����܂��C�Ⴂ�͂���܂��D
���̃y�[�W
��������蕪����₷���ł�👍
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���Ώ̂Ȑ}�`�ɂ��ā^20.05.14�n
�����y����ŕ��K���Ă��܂���.���肪�Ƃ��������܂�(*^^*)�������w���̍��̕��͂قƂ�NJo���Ă��Ȃ��̂ł����A�����玿�₪����܂����̂ł����ɏ������Ă��������܂��B�ɂƂ��ւ�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���Ώ̂Ȑ}�`�ɂ��ā^20.05.14�n
�����ł���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�_�Ώ̂Ȑ}�`�ɂ��ā^20.05.12�n
�Q�l�ɂ����Ă��������܂����I
���肪�Ƃ��������܂��I���i�O�Q�O���j��
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�P�����Ƒ������ɂ��ā^20.05.13�n
�萔���ɂ��Ă������ė~�����Ǝv���܂��B
���̑��͂ƂĂ�������₷���ǂ������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�萔���ɂ��ẮC���ȏ���Q�l���ł͂߂����Ɍ����Ȃ��C�т����肷��悤�Ȃ��Ƃ������Ă���̂ł����C�C���t���܂���ł������H
���w�Z2�N�������̋��ȏ��ł́C�����̉���͂���܂����W���̉����1�Ђ�����,�u�����Ɋ|����ꂽ���v���W���ƌ����ƂȂ��Ă��܂��D���̋��ȏ��͎����̉���͂��Ă��W���Ƃ͉����Ƃ�������Ȃ��ɌW���̘b�����Ă��܂��D�u�����Ɋ|����ꂽ���v���W���ƌ����u������Ղ��v�ł����C���Z�E��w�ł̏펯�ƈႢ�C�萔�����W���ɓ���Ȃ��Ə�������܂��D�e�C���[����,�t�[���G�����C1�̕����ɂ��Đ�������Ȃǂ������ʂŁC���Z�⊇�ʈȊO�Łu����̒��ڂ��Ă��镶���ȊO�̂��́v�͌W���ł��D���ɒ萔���͂˂ɌW���ł��D���������Ă���̂ł����C���t���܂���ł������H
���m�ʂ̕ł���̎���ɑ���n[�Q�_��ʂ钼���̕������ɂ��ā^20.05.11�n
�����͌v�Z���ƂĂ����ŁA�w�Z�̃h�����e�X�g�ƌ�������̂ɏo�肳��Ă������ŁA
2�_�i1.2�j�i3.8�j��ʂ�1����y=ax+b��a��b�̒l�����߂�B
�Ƃ�����肪����A�A���͂ł������̂�(1)�|(2)���c
�撣���Ăǂ����w���̂����L�ڂ���ĂȂ�������܂���ł����B
�����m��ҁn�F�A�����肪�Ƃ��D�u�撣���Ăǂ����w���̂��v�Ƃ͂ǂ��������Ƃ��q�ׂĂ�����̂�������܂��C�v����ɓ��T�C�g�̋��ނɑ��鎿��ł͂Ȃ��āC�h�����̖���������Ăق����Ƃ������Ƃł��傤���H���ʂ͓����܂��C�R���i�Ŋw�Z���x�݂ŁC�w�͒ቺ�����O����邨�肩��C��O�I�ɗ�����
2=a+b…(1), 8=3a+b…(2)
(1)−(2)
−6=−2a
a=3
�����(1)�ɑ��
b=−1
����āCy=3x−1…�i���j
���m�ʂ̕ł���̎���ɑ���n[�_�Ώ̂Ȑ}�`�ɂ��ā^20.05.10�n
�����`�ɂ��Ă��炦��Ƃ��ꂵ���ł�😊
�����m��ҁn�F�A�����肪�Ƃ��D�u�����`�v�Ƃ͉��Ȃ̂��C�Ӗ����ʂ��܂���
��?[����҂��^20.05.08�n
2a²�̌W���͂Ȃ�ł���
�����m��ҁn�F2
���m�ʂ̕ł���̎���ɑ���n[�������̍����ɂ��ā^20.05.01�n
�����g���������̍������m�肽��
�����m��ҁn�F�A�����肪�Ƃ��D�܂����߂ɁC
�S�����i���j�̃y�[�W�����Ă��������D
�K��������Ă����������肪�Ƃ�������܂����B�����䂤�����ȗ�����悤�ȋL���͒��w���̂����Ɋw�Z�ŏK�킹��ׂ����Ǝv���܂����l�I�ɁB����͂����Ǝ���Ȃ̂ł�����̏ꍇ�A�Ⴆ��720=��6�I�ƕ\�����ł��傤���H���������㎩�̂��܂������Ă��Ȃ��̂ŏȗ�����K�v�����邩����킩��܂���B�ł�����������ȗ�������Ȃ�K���������x�̐��܂Ŋo���Ă�����̂悤�Ȑ������o���Ƃ��ȗ��ł���̂ł͂Ȃ����Ǝv������ł��B���肢���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D

������

�Ƃ������Ƃ͌����܂����C�K��ŕ\���鐔���͌����Ă���C�L���g�����ł͂���܂���D������̕��͉��ɂł��i���������w�Z�ł�0�ȏ�̐��܂Łj�t���邱�Ƃ��ł��܂��D
���ɗ����܂�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝�ɂ��ā^20.04.30�n
�������悩�����ł�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���̑̐ρE�\�ʐ��ɂ��ā^20.04.29�n
�A���ł����Ƃ���TAP���ۂ���A���̑̐ς�\�ʐςȂ��ۂ�����Y��Ă��܂������A�ʼn_�Ɍ������o���悤�Ƃ���̂ł͂Ȃ��A�ǂ����������ł��̌������������̂��ǂނ����Ŏv���o�����Ƃ��o���܂����B���肪�Ƃ��������܂��I
�����m��ҁn�F�A�����肪�Ƃ��D
��?[�V�[������^20.04.28�n
�����̉��ɖ�肪����A���K���Ƃ��Ă������ǂ������ł��I
���[�g�̂��Ǝ��₵�����ł��B���[�g�̍��ɐ���������̂ł����A���ɐ�����u���̂͂Q�悵�Ă��鐔�����������ɂ����Ă����ł����H
�����m��ҁn�F�A�����肪�Ƃ��D���[�g�̉��ɐ���������Ƃ́C

�̂悤�Ȃ��Ƃł��傤���H

���Ɛq�˂Ă���̂ł���C�����Ƃ������܂����C�f�p�ɕ��ʂɍl����Ƃ��́C

��

��2�{��\���悤�ɁC

��

��2�{��

��\���ƍl���܂��D

��

��3�{��\���悤�ɁC

��

��3�{��

��\���ƍl���܂��D
�N�C�Y���ɂȂ��Ă���T�C�g�͌������Ɩ��������̂ŁA�L����������̂������ė~�����Ǝv���܂�����
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�_�Ώ̂Ȑ}�`�ɂ��ā^20.04.24�n
�ȒP������H�ԈႦ��z����́H
�����m��ҁn�F�A�����肪�Ƃ��D
�������s[�Ђ��邳��^20.04.23�n
������̕ҏW�͂���l�ł���Ă���̂ł��傤���B�o������͂������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D��l�ł��D���͂͂��肪�����ł����C��̓I�ɂ͂ǂ�Ȍ`�ł��傤���H
���m�ʂ̕ł���̎���ɑ���n[HTML�̊�{(1)�ɂ��ā^20.04.23�n
����ɂ���
�����ɂ���悤�ɁA�������ɃR�[�h���R�s�y����Chrome�œǂݍ���ł݂܂����B�ł����A��ʂ��^�����ʼn����\������܂���B�ǂ�����Ε\������邩�����Œ�����ƍK���ł��B
�����m��ҁn�F�A�����肪�Ƃ��D<body> </body>�̕����ɉ��������Ă��Ȃ���u��ʂ��^�����ʼn����\������܂���v�Ƃ����̂��������C������123�ȂǂƏ������ꂪ�\�������Ƃ������Ƃł�
���m�ʂ̕ł���̎���ɑ���n[��Βl�ɂ��ā^20.04.13�n
�����̐�Βl�͂ǂ����߂������������܂���c(*T^T)
3
- �Ȃǂ̐�Βl�͂Ȃ�ł����H
4
�����m��ҁn�F�A�����肪�Ƃ��D���̃y�[�W�ɂ���������̗Ⴊ�����Ă���܂����C

�̐�Βl�́C

�ŁC

�̐�Βl��

�ł��D�v����ɁC�u���̐��͕�����ς���v�����ł��D
���p���邱�Ƃ��ł��܂����B
���肪�Ƃ��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�A���������i���Z�������j�ɂ��ā^20.04.12�n
�킩��₷�������ł��A�L��������܂��B
���w2�N�y�A���������������(�܂Ƃ�)�z�����͂ł��܂���B
�@�@�@ �y�Ă�2�z�@�@�@�@�@�@�@�@�@�@ ���̖��ɐi�߂܂���B
��낵�����肢�������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�y�A���������������(�܂Ƃ�)�z→���͗��͍���Ă��Ȃ��y�[�W�Ȃ̂ŁC���͂ł��Ȃ��̂ō����Ă��܂��D
�y�Ă�2�z→�������܂���
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝�ɂ��ā^20.04.07�n
�ƂĂ����e���ڂ����A�������Ȗl�ł��ȒP�ɗ������邱�Ƃ��ł��܂����B���肪�Ƃ��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����̕ό`�ɂ��ā^20.04.07�n
���̐ԕ����̕����A�u�\�킵�Ȃ����B�v�ƂȂ��Ă��܂����A�������́A�u�\���Ȃ����v���Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D���艼���̕t�����@
������ �P�Ƃ̌�@1�@���p�̂����@�ʑ�1 ���e
���̌��,�i�@�@�j�̒��Ɏ����悤��,���p����̑O�̉��߂��瑗�邱�Ƃ��ł���B�\���i�\�킷�j
�ˁ@�ǂ���ł��悢
���͏��߂̕��͂킩��̂ł����A
���2����̒����Ȃ鎮�̂����Ђ���
�ǂ���������̂��킩��Ȃ��̂�
���̉�������肢���܂�(�M�E�ցE�L)
�����m��ҁn�F�A�����肪�Ƃ��D�{���ɂ�������ǂ�ł�������
���m�ʂ̕ł���̎���ɑ���n[�l���v�Z�̗D�揇���ɂ��ā^20.04.02�n
���N58�̎����n�Ǘ��E�ł��B�Z���̎l���v�Z�����ɂ����M�������Ȃ��Ă����̂ŁA�m��������Ӗ��Ŕ��ɖ𗧂��܂����B���ɉ��K���̎��H�����莩�M�����Ă܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���ʂ̕����̓����ƕ������̈Ⴂ�ɂ��ā^20.03.31�n
SPI�̕��Œ��w���w���w�ђ����Ă����w���ł��B
�Q�l���Ȃǂ�ǂ�ł��āA�u�������������]�����ǂ��ꕁ�ʂ̌v�Z�Ɖ����Ⴄ��H�v�ƍl�������������ʋM���̃T�C�g�ɂ��ǂ蒅���܂����B
���̃T�C�g�ł͕������ƍP�������ꂼ��̐����͂���̂ł����A���Ă���Ȃ��������_�〈�������ɐG���ׂ��Ƃ�����A���̂܂܃X���[����T�C�g�������A���Ǎ����B���Ȃ܂܂Ȃ̂ŎQ�l����ǂݐi�߂��ŏ�Q�ɂȂ��Ă��܂������Ă��܂����B
�ł����M���̃T�C�g�́A�P�����ƕ�����������������܂ł��Ă��邽�߂ƂĂ����ɂȂ�܂����B����ł���Ɨ����ł����C�����܂��B���ӂł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�ɂ��ā^20.03.31�n
�����₪�������ɂ�������
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�S�����i�p�[�Z���g�j�ɂ��ā^20.03.31�n
���肪�Ƃ��������܂�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�O�����̒藝�̉��p�ɂ��ā^20.03.30�n
�������݂̂ɐ����Ă���̂Ń��[�g�╪�������ƂȂ����������ق����ǂ�
�����m��ҁn�F�A�����肪�Ƃ��D����̂ɂȂ��悤�Șb������̂͂悭�Ȃ��ł��D�����̒��������̖��͍�����\���Ă��܂��DWeb��ʏ�ō������̂��������邱�Ƃ͓���C���̂悤�Ȗ��ɂ́C�قƂ�ǂ̐l���������Ȃ��ł��傤
���m�ʂ̕ł���̎���ɑ���n[�S�����i�p�[�Z���g�j�ɂ��ā^20.03.30�n
�ƂĂ�������₷���T�C�g�������Ē����L��������܂��B(o^o^o)
�����l�ŕ����͂��ǂ�܂��B
����ł����B���ꂩ������̗l�Ȃ��߂ɂȂ�T�C�g�����ꂩ��������Ă��������B
���̂��߂Ɍ����₻�̑��F�X�撣���ĉ������B
�Ō�ɂ������A���̗l�Ȃ��߂ɂȂ�T�C�g�������Ē����{���Ɋ��ӂ������܂��B�L��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���̒l�ɂ��ā^20.03.29�n
X��〜�̎����Ȃ��ꍇ�ǂ���������ł����H
�����m��ҁn�F�A�����肪�Ƃ��D���w�Z�ł͂����������͏o�܂���D�Ⴆ�C�i�������m���Œl�������ĂȂ��Ƃ��j�u2x+1�̒l�����߂�v�ƌ�����肪�o����C���Ă������悢
���m�ʂ̕ł���̎���ɑ���n[�����̐����ɂ��ā^20.03.19�n
����邱�Ƃ������Ă�����
�Q�l�ɂȂ�܂����B
���肪�Ƃ��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����̕ό`1�ɂ��ā^20.03.17�n
���܂����킩��Ȃ������ł��B���݂܂���B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�ω��̊����ɂ��ā^20.03.17�n
���肪�Ƃ��������܂��B
�悭�킩��܂��� �B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Β��p,���ʊp,���p�ɂ��ā^20.03.14�n
�����������p�I�Ȗ����o���Ă����������炤�ꂵ���ł�
�����m��ҁn�F�A�����肪�Ƃ��D��{���������Ă���y�[�W�ɂ͊�{�I�Ȗ�肪����C���p���������Ă���y�[�W�ɂ͉��p�I�Ȗ�肪����܂��D���̋t�ł͂���܂���D���R�̂��Ƃł��D
���m�ʂ̕ł���̎���ɑ���n[�H�����̔Z�x�ɂ��ā^20.03.08�n
�Z�x�̖��ł�����Ƃ��������ō����Ă����ł������v�ł����H�H�����������ł��B
�Z�x10%�̐H�����Ɛ��������ĔZ�x7%�̐H����200g����ɂ͔Z�x10%�̐H�����Ɛ�����g��������Ηǂ����Ƃ������Ȃ�ł����ǂ̂₤�ɂ����炢���ł����H
�����m��ҁn�F�A�����肪�Ƃ��D10%�̐H����x(g)�Ɛ�200−x(g)�̍��v200(g)���������7%�̐H����200(g)�ɂȂ�Ƃ����
�H���̏d����0.1�~x(g)
�H�����S�̂̏d����200(g)
�����7%�ɂȂ�̂�����C0.1�~x��200=0.07 → x=??
����������Ɩ{�l�̍l����͂����Ȃ��Ƃ悭�Ȃ��̂ŁC���̃y�[�W�̉��̕��ɂ��鎩�R������B�Łu10%�̐H����100(g)�ɐ�100(g)�v����X�^�[�g�����5%�̐H�����ɂȂ�D���������Z������ɂ́u10%�̐H����110(g)�ɐ�90(g)�v������Č���D��������Ƃ���Z���Ȃ��āC2�C3���7%�̐H�����ɂȂ�D--���R�̂��ƂȂ���C10%�̐H����x(g)�Ƃ����Ƃ��ɐ���200−x(g)�Ƃ��Ȃ���Ȃ�Ȃ��D
�킩��₷������ƂƂ��ɍŌ�Ɏ��H�����邱�Ƃɂ��A�͂���������Ƃ����H�v�A�f���炵��
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�O�p�ɂ��ā^20.03.02�n
��ϕ��ɂȂ�A������܂������A�Ȃ�ŐԂ�������~�܂Ȃ��̂ł����H
�����m��ҁn�F�A�����肪�Ƃ��D�Ԉ���Ă���ꍇ�C�������Ă̏ꍇ�C������x����̃{�^�����������ɓ����������ւ����ꍇ�͋������܂܂ł�
���m�ʂ̕ł���̎���ɑ���n[�Ώ̈ړ��ɂ��ā^20.02.28�n
���Ώ̂̐}�`�Ƃ͌������A���Ώ̈ړ��Ƃ͌���Ȃ�
�����m��ҁn�F�A�����肪�Ƃ��D�w�ԑ��̗���łȂ��ċ����鑤�̗��ꂩ��̔����̂悤�ł��D�p���̖��_�͈ȑO����F�����Ă��܂����C������Ղ���ʂ��邽�߂ɂ����Ďc���Ă��܂��D���́C���Ȃ����Ԉ���Ă��܂����u���Ώ̂̐}�`�v�Ƃ͌����܂���D���w�ł��C���w�Z�ł��u���Ώ́v�Ƃ����p��͂���܂���D���̋��ނł́C�_�Ώ̂Ɓi���j�Ώ̂̂Q���Ɉ����Ă���̂ŁC�������Ȃ��悤�ɁC��ʂ��Ă��邾���ł��D
���m�ʂ̕ł���̎���ɑ���n[�����̐����ɂ��ā^20.02.26�n
������₷�����������A�N�C�Y�ł��𗧂��܂����̂ŗǂ������Ǝv���܂��B�����Ē������肪�Ƃ��������܂���
�����m��ҁn�F�A�����肪�Ƃ��D
���_�ސ쌧[?����^20.02.25�n
HTML�̊�{�A�ɂ��܂��đ����̂��ԐM���肪�Ƃ��������܂��B
�͂��A�g���q��html�ɂ��Ă��܂������A�O�̂���htm�ɕς��čĎ��s���Ă݂܂������A���ʂ͓����ł��B�ʐ^���̏ꍇ��upload�����܂����A�����������Ƃ͕K�v�Ȃ��̂ł���ˁH
���݂ɁA��PC��Windows10Home�ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�Q�O�N�قNJԂɁC�l�b�g���q����Ȃ��Ƃ������[�U�Ɂu�p�\�R���̊���ς��Ă��������v�Ƃ�������C�����̑����J����ꂽ�Ƃ������Ȃ��b���������D���l�̃p�\�R���̎��s���́C���t�����ł͓`��炸�C�Öق̑O�Ⴄ�ꍇ������D�i�Ⴆ�C�����̃u���E�U�ŁC�Z�L�����e�B�̊ϓ_���烍�[�J���t�@�C���̃X�N���v�g�͎��s�ł��Ȃ��悤�ɂȂ��Ă���Ȃǁj
�@�A�h���X����c:\ �Ə�������ŁC�����̕ۑ������t�H���_�̂��̃t�@�C�����m���ɓǂ�ł��܂����H�@�AHTML�t�@�C�������������Ă��\���������ŕς��킯�ł͂Ȃ��D�u���E�U�Ń����[�h���Ȃ��ƕ\���͕ς��Ȃ��@�B�u�������p�\�R�����ł́A���̕��͂͌���܂��B�v�Ƃ͂ǂ������Ӗ��Ȃ̂��D�e�L�X�g�t�@�C���̒��Ō����Ă��Ă��C���̃e�L�X�g�G�f�B�^�ŕۑ��������݂��Ă���C�u���E�U�Ń����[�h���Ȃ���Ή����X�V����Ȃ��Ƃ����̂́C�������Ă��܂����H
���m�ʂ̕ł���̎���ɑ���n[HTML�̊�{(1)�ɂ��ā^20.02.24�n
�v���O���~���O���w���K�C�̎�����A�O���~���O�Ƃ͉�����H�������K�ł�����̂Ȃ班���͂������Ă݂悤���A�Ǝn�߂Ă݂܂������A������ςȂ��炵�������Ă��܂��B���K�P�̎w���ʂ�p�\�R�����ɕۑ����Achrome�ł��̃t�@�C�������Ăяo(�������ɓ��������̂ł���ˁH�j���Ă��A�^�����ł��B���g���Ȃ����炩�ƁAbody�����ɕ��͂����Ă�chrome�ł͕ω��Ȃ��ł��B�������p�\�R�����ł́A���̕��͂͌���܂��B�S���̏��S�҂̂��߁A�I�Ȃ�����⑀������Ă��邩������܂��A��w�쒸����ƍK���ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�g���q��htm�ɂ��Ă��܂����H�Ⴆ�Cabc.htm
���m�ʂ̕ł���̎���ɑ���n[�P�����Ƒ������ɂ��ā^20.02.23�n
���1�ɂ��ĂȂ�ł����A�ǂ��̌W������������Ȃ��̂ŁA����������Ƃ����Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�u���̒P�����̌W�����Ă��������B�v�Ə����Ă���̂ňӖ��͂͂����肵�Ă��܂��D�Ƃ��������C���Ȃ��͖���ǂ�ł��Ȃ��\��������܂��D�u�͂��߂ɖ����P�I�сv�Ə����Ă���̂ŁC���߂ɖ���I�Ȃ���Θb���n�܂�Ȃ��̂ł��D����I�ׂΌW�������܂�̂ł��D
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝(�������)�ɂ��ā^20.02.22�n
������肪��������܂����B�����Ɩ��𑝂₵�Ă��������B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�P���������̕��͑��ɂ��ā^20.02.11�n
4%�̐H������ 16�i%�j�̐H������������� 14�i%�j�̐H������ 96�ig�j�ł����D���ꂼ��̐H���������ig�j�����������D�Ƃ������œr���o�߂�1�ԍŌ�̓������}�ɉB��Ă��܂��Ă���
�����m��ҁn�F�A�����肪�Ƃ��D���̋��ނ�PC�p�ŁC�X�}�z�œǂނ��Ƃ͑z�肵�Ă��܂���D�ǂ����Ă��ǂ݂����ꍇ�́C�������ɂł��ǂ߂�ݒ�ɂ��āC��ʂ��������ɂ��Ă��������D
���m�ʂ̕ł���̎���ɑ���n[�Β��p,���ʊp,���p�ɂ��ā^20.02.09�n
�ȒP�����܂�
�����Ɠ�����Ă��������B
�����m��ҁn�F�A�����肪�Ƃ��D�₳�����y�[�W�͂₳�����D����y�[�W�͓���D
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝(�������)�ɂ��ā^20.02.09�n
�ƂĂ��ǂ��ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝�ɂ��ā^20.02.08�n
������₷���B
��2�Ȃ̂Ƀe�X�g�͈͂ɓ����Ă��̂ŏ�����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�f���������Ƃ��ɂ��ā^20.01.29�n
���w���ƂĂ����ł����A�w�тȂ������������Ǝv���āB�������A�����ɂ��ǂ蒅���܂����B���������̂��N���b�N����Ɛ�����s�������킩��̂ƁA������킩��₷���Ă����Ǝv���܂����B���̕�����w�K�������Ƃ����܂��B���ӂȃW���������킩��̂����C�ɂȂ���Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�O�p�ɂ��ā^20.01.29�n
����̕\�������ɂ킩��ɂ����B
�����Ă��̂悤�Ȃ킩��ɂ����\��������̂ɂ͖���̂ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D��ł��i�������āj�ō̓_����������C���̂悤�Ȋ��z�����炤���Ƃ�����܂��D
���m�ʂ̕ł���̎���ɑ���n[�����i�S����,����,�����j�ɂ��ā^20.01.28�n
��ς킩��₷���q�ǂ��ɂ��\�������ł��܂����B
��������肾�����̂ł����A�����ł��y�����Ȃ��Ă��������ł��B
���肪�Ƃ��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[��`�̖ʐ��ɂ��ā^20.01.28�n
�킩��ɂ����ł�
�킩��Ȃ��l�ɂ����������킩��₷���������낵�����肢���܂�
�����m��ҁn�F�~�̖ʐς̔����́C�~�̖ʐς̔����ł��D���Ɍ�����������܂����H
���m�ʂ̕ł���̎���ɑ���n[�������ɒ������K�ɂ��ā^20.01.19�n
���́[
0.25�̏ꍇ�́c
�����m��ҁn�F
�Ƃ肠�������Ă����ۂł���Ă����ƒN�ł��ł��邩�炻���͂�����Ǝv���B
�����m��ҁn�F�A�����肪�Ƃ��D�u�N�ł��v�Ƃ͌����Ȃ��ł��傤����Q�[���ł��ł��鎞�ԂɁC����ȃT�C�g��T���ē����ė���l���C�C���`�L���Đ������Ă��C���̓��ɂ��Ȃ�Ȃ����Ƃ��������Ă���̂�����C���̉\���͂Ȃ��ł��傤
���m�ʂ̕ł���̎���ɑ���n[��`�̖ʐ��ɂ��ā^20.01.12�n
�����A�g�킵�Ă�����Ă��܂�🙇��
��肪��R����A�ƂĂ������Ǝv���܂�!!!
���������A�킩��Ȃ��l�ɂƂ��Ă͊������ł�w
�����Ă�����A�V�C�ŕ\���̂��ʔ����ėǂ��ł���👍���ꂩ����A�撣���ĉ������I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�O�p�`�̖ʐς̓����ɂ��ā^20.01.11�n
��6�̉ŁA�_A�̍��W���r������i�R�C�R�j�ƂȂ��ĉ�����Ă��܂��B�_A�́A��蒆�ł́i�R�C�S�j�ł��̂ŁA����AB�Fy���i5/�S�jx�{1/�S�ƂȂ�A�́A�i2,11/4�j�ƂȂ�ׂ��ł͂Ȃ��ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D�������܂����i���̕����I�j
���m�ʂ̕ł���̎���ɑ���n[�Ă��ɂ��ā^20.01.10�n
�����킩��Ղ��ł��B��l�����ǁ@�߂��Ꮥ����܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝(�������)�ɂ��ā^20.01.09�n
�ƂĂ��킩��₷���I
�������Ă����̂łƂĂ��ǂ������ł��I
���ꂩ������p���Ă��������Ǝv���܂�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����}�`�ƕӂ̔��ɂ��ā^20.01.08�n
�v�_���Ȍ��ɂ܂Ƃ߂Ă���̂ŁA���̌�̖��������ɓ������Ė𗧂��܂����B
�S�̓I�ɂ킩��₷���ď�����܂����I
�����m��ҁn�F�A�����肪�Ƃ��D
�����Ɍ��m�肨����^20.01.07�n
�s�������܂����������炸�A�����Ă������Ɍ������I
�w�N���e�X�g�Ɍ����Ă̖��������ė~�����ł��I
���P�ƒ��Q�ł����Ă��������܂����H
�����m��ҁn�F�A�����肪�Ƃ��D���̋��ނł́C�ڎ��̊e�w�N�̏I���̏��ɁC�܂Ƃ߂̖�肪����Ă���܂��̂ŁC�Q�l�ɂ��Ă��������D�����C���ۂɂ͂��ꂼ��̒��w�Z�ŁC�����Ă�����e�͂��Ȃ�Ⴄ�ƍl�����܂��̂ŁC�������g���Ă��鋳�ȏ��͖̏����Ȃǂ�����������x�������킹�₷���ł��傤�D
���m�ʂ̕ł���̎���ɑ���n[�������������ƂȂ邎�̒l�ɂ��ā^20.01.06�n
��250-3���B3���܂Łオ�������Ă��܂��B��ƂȂ�悤��n��3�Ԗڂɑ傫�����R���������߂Ȃ����B���肢���܂�
�����m��ҁn�F�\���킯�Ȃ��ł����C���Ȃ��͒��w���ł����Z���ł��Ȃ��悤�ł��D�v���O���~���O�̉ۑ�ōs���l���Ă���̂ł�����C����JS�R�[�h���e�L�X�g�t�@�C���œǂݎ���āC�������̃v���O���~���O����̃R�[�h�ɒ����Ă��������D
count = 0;
for(n=Math.floor(250/3);n >0; n--)
{for(m=1; m< Math.sqrt(250); m++)
{if(250-3*n==(2*m-1)*(2*m-1))
{count++;
if(count == 3)
{document.getElementById('for_disp').innerHTML = 'n='+n+',m='+m;
break;
}
}
}
}
���m�ʂ̕ł���̎���ɑ���n[�Q���r�ɂ��ā^20.01.05�n
���݂܂���B�Ⴆ�A3�|��6�ƁA2�|��2�̑召�W�ׂ�Ƃ��A�Q���悷��Ɗe�X�A15�|6��6�A6�|4��2�ƂȂ�̂ł����A���̏ꍇ�A�����������������������āA15�|6��6�A15�|4��2�|9�Ƃ��A15�|��216�A15�|(��32�{��81)�Ƃ�����A������Ȃ��Ȃ�܂����B���̂悤�ɁA�������܂��ɋ��ʂ��鐔���܂܂�Ȃ����A�����Z�����Ē��ׂ�̂������葁���̂ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D�����̋ߎ��l�Ŕ�r����ƁC3�|��6=3�|2.449...=0.551..., 2�|��2=2�|1.414...=0.586..�ƂȂ��āC3�|��6<2�|��2�������܂��D�Q���r�Ȃǂ̐����v�Z�ŏؖ�����ɂ́C��߂��܂��D
���m�ʂ̕ł���̎���ɑ���n[��}�i�������j�ɂ��ā^20.01.04�n
���T�D�Q�ɂ���
�~�̒��SO�����߂���̕ʉ��B
A�𒆐S��OA�a�Ƃ���ʂ�`���A��AB�Ƃ̌�_��C�Ƃ���BAB:AC=2:1�Ł�ACB=90�x������A�O�p�`ABC�́�ABC��30�x�Ɏ����p�O�p�`�BB�𒆐S�ɓK���Ȍʂ�`���AAB,BC�Ƃ̌�_�����ꂼ��D,E�Ƃ���BD,E����K���Ȍʂ�`�����̌�_��F�Ƃ���B����BF�ƌ�AB�Ƃ̌�_��P�ł���B
�����m��ҁn�F�A�����肪�Ƃ��D�ʉ����l�����Ƃ������Ƃ̂悤�ł����C�uD,E����K���Ȍʂ�`�����̌�_��F�Ƃ���v�Ƃ́C����\���̂��s���ł�
���m�ʂ̕ł���̎���ɑ���n[�������������ƂȂ邎�̒l�ɂ��ā^20.01.04�n
�킩��₷�����������A��������̂ł��������ɂ����܂����I�I���肪�Ƃ��������܂����I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�f���ɂ��ā^20.01.04�n
������}��������₷������
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝(�������) �ɂ��ā^20.01.02�n
�����������₷�������I�I
�ǂ��������肪�Ƃ��������܂�m(*_ _)m
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[��}�i�������j�ɂ��ā^19.12.28�n
�ǂ��Ƃ���́A��������Ă��āA���̉����������₷���Ƃ������Ƃł��B
��Ăł����A������Ȃ������摜�Ȃǂő����āA�������������Ă��炤�Ƃ����̂͂ǂ��ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��D�㔼�̒�āF�����ł��D���̗��R�F���̃y�[�W�ɏ����Ă���}�ɂ��ẮC����ɓ����܂����C���̏ꍇ�͐V���Ȑ}�𑗂��Ă��炤�K�v�͂Ȃ��D���̃y�[�W�ɂȂ��}�̏ꍇ�C�l�Ԃ̒ʐM�ł͋�������b�ł��C���̉����ނƂ��Č��J����Ƃ��ɁC���̎���̐}�����쌠�@�ɒ�߂��Ă���u���J����Ă��镶���̏o�����������p�v�Ƃ����v�������Ă��邩�ǂ������C���f�ł��Ȃ����k����������ł��D
���m�ʂ̕ł���̎���ɑ���n[�H�����̔Z�x�ɂ��ā^19.12.27�n
���������ɗ����܂���😊
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�O�ӂ̒������^����ꂽ�O�p�`�ɂ��ā^19.12.26�n
���m�ʂ̕ł���̎���ɑ���n[�P���������y a�̒l �z�ɂ��ā^19.12.24�n
����Ė���Ă�̂ɐ\����Ȃ��ł����r���v�Z���A�ׂ������Ăق����ł��B
������ȗ������ƁA�킩��Ȃ��ł�
�����܂���B���P�̕��X�������肢���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D����{�^�����N���b�N����Ή�����o�܂��D����ȏ�ׂ������Ă�������₷���͂Ȃ�܂���
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝(�������) �ɂ��ā^19.12.22�n
�ƂĂ����������������Ƃ��o���܂���
�����m��ҁn�F�A�����肪�Ƃ��D���������ł���l�̊��z���Ǝv���܂�
���m�ʂ̕ł���̎���ɑ���n[�Β��p,���ʊp,���p�ɂ��ā^19.12.18�n
�����܂ł킩��Ȃ��Ƃ����킯�ł͂Ȃ��ł����A�������K�ł����������Ƃ��ɑS�������ƁA�ԈႦ���Ƃ��̔������킩��Ȃ����炠���Ă�̂�������Ƌ^���Ă��܂��܂��ˁB
�C���X�g�̉��ɕ����𑫂��Ă��悢�̂��ȂƎv���܂�
�����m��ҁn�F�A�����肪�Ƃ��D�����̏ꍇ���듚�̏ꍇ��������o��̂ŁC����ŕ�����͂��ł��D
���m�ʂ̕ł���̎���ɑ���n[���s���Ɗp�ɂ��ā^19.12.17�n
��2���q�ł��I���͏m�ȂǂɌ����ĂȂ����߁A���̂悤�ȗ��K���͂ƂĂ����ɗ����܂��I���肪�Ƃ��������܂��I
�����m��ҁn�F�A�����肪�Ƃ��D�M�҂��m�ɂ͍s���Ȃ������i�N�オ���Ȃ�Ⴄ������j
���m�ʂ̕ł���̎���ɑ���n[�O�����̒藝�̉��p�ɂ��ā^19.12.15�n
������ƂĂ��ǂ�������܂����I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�_�Ώ̂Ȑ}�`�ɂ��ā^19.12.14�n
�ƂĂ�������₷�������ł�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝�ɂ��ā^19.12.14�n
�g���₷�������ł��A��������̂悤�ȃT�C�g������Ă��������ˁB
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Β��p,���ʊp,���p�ɂ��ā^19.12.10�n
�킩��₷������
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝�ɂ��ā^19.12.09�n
�悩�����ł�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�f���������̉��p�ɂ��ā^19.12.09�n
�ƂĂ�������₷���������ł����B
���͂��̖��őf���������̉��p�𗝉����邱�Ƃ��o�����̂łƂĂ�������܂����I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������̍����ɂ��ā^19.12.09�n
���̂悤�ȕ��͖������ȏ��Ȃǂɂ����Ƒ��₵�Ăق����ł��B
�Ȃ��Ȃ�A�������Ǝ����I�ɃL�c�C��������Ȃ��ł������̕������k�݂̂�Ȃ̕������ւ̗������[�܂�A�݂�Ȃ����͖������������ŁA�������������ŗ��āA�����������悤�ɂȂ�Ǝ����͎v���܂��B
���w�����Ȑl�������Ǝv���̂ŁA����Ȓ�Ăŗǂ���A���ɗ��ĂĂ���܂��Ɗ������ł��B��낵�����肢�����܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�_�Ώ̂Ȑ}�`�ɂ��ā^19.12.07�n
�_�Ώ̂�������܂���ł������A���̃T�C�g�ŗ����ł��܂����B�}���������A���p��������A������₷�������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���̕ψ�(�������)�ɂ��ā^19.11.27�n
�u���2
y�̕ψ��a��x��b�ł���v
�l���y�̕�����x�ɂȂ��Ă܂�
�������肢���܂�
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�H�����̔Z�x�ɂ��ā^19.11.25�n
���K���x�ɂ͂��傤�Ǘǂ�����
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���s���Ɗp�ɂ��ā^19.11.23�n
�ƂĂ��ʔ���������ł�育����������܂����I���Ȃ݂ɑS����ł���‼������[✨
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�S�����i�p�[�Z���g�j�ɂ��ā^19.11.21�n
������₷����������Ăė������₷�������ł��B�S��ԈႦ���ɉ����܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������������ƂȂ邎�̒l�ɂ��ā^19.11.19�n
�ǂ̎Q�l���ɂ��A�������ڂ����ڂ��Ă��Ȃ�����ǁA���Ƃ��ďo�Ă��Ă��܂��āA�����Ă��܂����B�ł����A�����ɂ́A�킩��Ȃ�������肪�S�������āA������������₷���������Ă��������Ă����̂ŁA�{���ɂ��肪���������ł��B����͂̂Ȃ������ł��A�ȒP�ɉ������Ƃ��ł��܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝�ɂ��ā^19.11.15�n
���p�̖�肪�Ȃ������̂ŏo���Ăق����ł�
�����m��ҁn�F�A�����肪�Ƃ��D�~���p�̒藝�̃y�[�W�ɂ͉~���p�̖�肪�����Ă���C���p�̖���
���s���Ɛ}�`�̃y�[�W�ɏ����Ă���܂��D�~���p�̃y�[�W�ɍ��p�̖��͂���܂���…����������K�v������܂����H
�@
�w�����ڎ���ǂ܂Ȃ��Ȃ����Ɩ�ˋ������Q���Ă�����D
��������Ƃ������������̂łƂĂ�������₷���A���ɂȂ�܂����B
�܂��A�q���g���������肠�����̂ł悩�����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������ɒ������K�ɂ��ā^19.11.14�n
��l�ɂȂ��ĂӂƁA�킩��Ȃ��Ȃ����̂ŃR�R�֔��ł��܂����B
�y�[�W���S�Ă��V���v���ʼn�����킩��Ղ�������������A�������N���b�N���Ă����ɂ킩�邱�ƂɊ������܂����B
�����q�ǂ����ł������ɂ͂��Ћ����Ă��������ł��I
���肪�Ƃ��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝�ɂ��ā^19.11.13�n
���w3�N�ł��B���A���̉~���p�̏͂̕������Ă��܂��B
�܂��A���̃T�C�g�Ɣ�ׂĖ��������₷���B�q���g������B�킩��Ȃ��Ƃ��͉�������遨�����͂��ǂ�B
��l���̃l�^�ɂ��Ȃ�܂�♡
�����m��ҁn�F�A�����肪�Ƃ��D
���m? �^������������^19.11.12�n
�������̉��������킩�炸���܂����B
�ƂĂ��킩��₷���ĉ�����悤�ɂȂ�܂����B
�������Ńe�X�g�������_�����܂����B
�{���ɂ��肪�Ƃ��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�A���������ƃO���t�ɂ��ā^19.11.10�n
���K���������Ƒ��₵�ė~�����ł��I
�����m��ҁn�F�A�����肪�Ƃ��D����̖�肪�U�肠���āC�e�X��5�̏���ɂȂ��Ă���̂ŁC�\�������ƍl���Ă��܂�
���m�ʂ̕ł���̎���ɑ���n[�������ɒ������K�ɂ��ā^19.11.03�n
16.5���ɒ������@���킩��܂���
�����m��ҁn�F�A�����肪�Ƃ��D���������邱�Ƃ͂ł��܂����C���̃y�[�W��25���ԓǂ�ł���C�Ȃ������̎��₪����Ƃ������Ƃ́C�����g�ɒ����Ȃ������Ƃ������ƂɂȂ�̂ł͂Ȃ��ł��傤���H

������킩��₷������
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Β��p,���ʊp,���p�ɂ��ā^19.10.30�n
�ƂĂ�������₷���ł��I�I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�O�����̒藝�ɂ��ā^19.10.27�n
������������킩��₷�������ł�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�P���������̕��͑�i���ĕt:���j�ɂ��ā^19.10.27�n
�����͕������̕��͑肪���Ȃ̂ő��̃T�C�g�ł��������������Ă��̃T�C�g�ŏ��߂ĉ������̂ł������������C���ɂȂ�܂����B����ƍׂ��������Ȃǂ��܂܂�Ă���킩��₷���̂ł��������ɗ����܂���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���̒l�ɂ��ā^19.10.27�n
�[5b���̎��̒l�͂Ȃ�ł����H
�����m��ҁn�F�A�����肪�Ƃ��D���̃y�[�W�ɂ����������Ƃ͏����Ă���܂���D���̃y�[�W�ɊW�̂Ȃ��C���Ȃ��̏h��̓������Ă���̂ł����H
���������C���w1�N���x����

�̒l���������ɁC

��
^2&chf=bg,s,fff9f9)
�̎��̒l��₤���Ƃ͂Ȃ��ł��傤�D���̖����悭�ǂ�ł��������D
���S�p��180�x�ȏ�̏ꍇ�̉�������肢�������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�������M���܂���
���m�ʂ̕ł���̎���ɑ���n[�ω��̊���(�������)�ɂ��ā^19.10.18�n
��������������킩��₷�����Ăق����ł��B
�ł��A�������킩��₷���������Ńe�X�g���ɖ𗧂Ă܂����B���肪�Ƃ��������܂��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝�ɂ��ā^19.10.18�n
�ł����ق��ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�P���������̕��͑�i���ĕt:���j�ɂ��ā^19.10.17�n
���킩��₷��
�����m��ҁn�F�A�����肪�Ƃ��D��
���m�ʂ̕ł���̎���ɑ���n[�����`�̕������ɂ��ā^19.10.17�n
�������̓����ŕ����ɂȂ�p�^�[���̏ꍇ�������Ă�������
�����m��ҁn�F�A�����肪�Ƃ��D�������̓����ŕ����ɂȂ�p�^�[���̃y�[�W������Ă��āC�u�������̓����ŕ����ɂȂ�p�^�[���̏ꍇ�������Ă��������v�Ƃ�������E�v�]���̂́C��Ȃ��Ƃł��D���̃y�[�W������������D
�@����Ƃ��C�W���������̖��ŁC�������ɂȂ�̂͂ǂ�ȏꍇ���Ɛq�˂Ă���̂Ȃ�

�̂悤��6��3�̔{���ɂȂ��Ă���Ƃ��́C��

�̂悤�ɐ����ɂȂ�

�̂悤��5��3�̔{���ɂȂ��Ă��Ȃ��Ƃ��́C��

�̂悤�ɕ����ɂȂ�ƌ����܂�
�\���́A�����p�[�Z���g�ɂ����
�����m��ҁn�F�A�����肪�Ƃ��D�w�Z��m�̏h��̓�����q�˂Ă���̂ł͂Ȃ��ł��ˁD8��50=0.16������16(%)
���m�ʂ̕ł���̎���ɑ���n[�P���������̕��͑�i���ĕt:���j�ɂ��ā^19.10.13�n
�e�X�g�Ɍ����Ă������𗧂��܂����B
���肪�Ƃ��������܂���❗
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������̕\�����ɂ��ā^19.10.09�n
a*(-3)�̕�����
�����m��ҁn�F����Ȃ̂��C�ӌ��Ȃ̂�����Ȃ���Ε�����܂���Da*(-3)�̕��������Ԉ���Ă���ƌ����Ă���̂��C������Ȃ����狳���Ăق����ƌ����Ă���̂��H
���m�ʂ̕ł���̎���ɑ���n[�i���o�[�v���[�X�ɂ��ā^19.10.08�n
�S�ėǂ�
������₷���w�Z�̐搶���ǂ�
�����m��ҁn�F�A�����肪�Ƃ��D�w�Z�Ő��Ƃ������܂����H
���m�ʂ̕ł���̎���ɑ���n[�����̕ό`�ɂ��ā^19.10.08�n
���̂Ƃ���ŁA���������L�����Ă���̂ɁANO�Ƃ����o�܂���B����͋@��̖��ł��傤���H�Ȃ��������������L�����Ă���̂�NO�Ƃ����o�Ȃ��̂������Ē��������ł�...
�����m��ҁn�F�A�����肪�Ƃ��D�������œ�����ׂ�����啶���œ�������C���p�����œ�����ׂ��Ƃ����S�p�����œ���ƁC�_���ł��D��������CiPhone��PC�p�̋��ނ�ǂނ͖̂����ł��傤�H
���m�ʂ̕ł���̎���ɑ���n[�P���������̕��͑��ɂ��ā^19.10.07�n
���͂��ƂĂ��킩��₷��
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�l���v�Z�̗D�揇���ɂ��ā^19.10.05�n
9�Ԃ̖��ł���-2�̓����������Ƃ���-2�~(-2)��4�ɂȂ�Ǝv�����̂ł���-4(-3)����-(-12)�ƂȂ��Ă��̂ł����悭�킩��Ȃ������̂ʼn�������肢�������ł�
�����m��ҁn�F�A�����肪�Ƃ��D�����ɏ����Ă���ʂ�C�Q��̌v�Z���ɍs���܂��i2^2=4�ł��D�����͌�ŕt���܂��D−2^2=−4�ł��j
���m�ʂ̕ł���̎���ɑ���n[�Ή��\�ɂ��ā^19.10.04�n
�o�Ȑ���1����Ȃ��Ă����ȃp�^�[���̂��o���Ăق����ł�
�����m��ҁn�F�A�����肪�Ƃ��D���̃y�[�W�́C�o�Ȑ��̋��ނł͂Ȃ��āC�������̋��ނł��D�܂��C���w�Z�̋��ނł́C���_�����_�ɂ�����̂̂ݎ�舵���܂��D����ȊO�̂��̂��K�v�ȏꍇ�́C���Z�̋��ނ̕������Ă��������D
���m�ʂ̕ł���̎���ɑ���n[�Q���������̉������i�܂Ƃ߁j�ɂ��ā^19.10.03�n
��ς킩��₷���ĂƂĂ�������܂��A���肪�Ƃ��������܂�_(._.)_
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�P���������̉������ɂ��ā^19.10.01�n
�|X�|5X�̉�����������Ă��Ȃ��Ă킩��Ȃ�����
�����m��ҁn�F�A�����肪�Ƃ��D���̌`�̎����ӌ��͂悭����܂����CGoogle�̌����ŏo�Ă�����̂������̒��ׂ������̂��Ƃ͌���܂���D�ꎟ�������̃y�[�W�������ł悭�q�b�g����̂ŁC���̃y�[�W����ɏo�Ă��邩������܂��C���Ȃ��̒��ׂĂ�����̂͂P���������ł͂���܂���D���������C�u�|X�|5X�̉������v�Ƃ������̂͂���܂���D�|X�|5X=�|6X�̂悤�ɕό`����̂́C���̕ό`�Ƃ������P�̂P�w���ɏK���b�ł��D����ɑ��Ă��Ȃ������Ă���y�[�W�͂P���������̃y�[�W�ł�.�u�|X�|5X��12�̉�������X=�|2�v�͂���܂��D�u�|X�|5X�̉��������Ȃ��v�u�|X�|5X�̌W���̂܂Ƃߕ����|6X�v�̈Ⴂ�ɒ���
���m�ʂ̕ł���̎���ɑ���n[�f���������ɂ��ā^19.10.01�n
2�̐����������Ƃ������Ƃ́A���҂Ƃ��f���������������ɁA�f�����A�����Ă��̐����������Ƃ�����̂ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D�����܂����f���������̈�Ӑ��ƌ�����d�v�Ȑ����ł��D
���m�ʂ̕ł���̎���ɑ���n[��@�̌����ɂ��ā^19.09.30�n
����ȊO�ɂ������ĕ����Ă��̂ł��������o���Ȃ������̂ł�������͈�ԕ�����₷�������ł��܂����I�I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�A���������̍���������͑��ɂ��ā^19.09.29�n
�I�𐔂�����
�����m��ҁn�F�A�����肪�Ƃ��D�܂��ꓖ�����h�����߁C6����x�͑����Ȃ��ł��傤�D5�͏��Ȃ���6�͑����Ƃ́C�đq���b�l�����Ă�����Ċ�Ԃ����H
���m�ʂ̕ł���̎���ɑ���n[�������ɒ������K�ɂ��ā^19.09.29�n
���肪�Ƃ��������܂�😊
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����̕��s�ړ��ɂ��ā^19.09.28�n
�܂����������肸�炩����
�Ȃɂ��킩��Ȃ�
������������
�킩��Ȃ��N�\
�����m��ҁn�F�A�����肪�Ƃ��D�l�̌��ɂ́C���܂�Ȃ���ɂ��ĕ��������Ă�ƌ����Ă���D���t�͐l�������邾���łȂ��C�������g��������D�N�\���t���g��Ȃ��悤�ɂ��āC�y���������Ă�������
���m�ʂ̕ł���̎���ɑ���n[�s�����ɂ��ā^19.09.27�n
�����ԈႦ�����A������Ƃ����q���g���o���Ă��ǂ�����
�����m��ҁn�F�A�����肪�Ƃ��D�쐬�����́C���Ɖ̊Ԃɂ�1�s������Ȃ��Ǝv���܂����i=�q���g�������ΉɂȂ�j���C���l�����1�s���炢�͏����邩������܂���D�����lj����܂���
���m�ʂ̕ł���̎���ɑ���n[���̒l�ɂ��ā^19.09.24�n
�����ƕ��������̂ŐV����������Ă�������
�����m��ҁn�F�A�����肪�Ƃ��D���Ȃ���Android�g�т�PC�p�̃y�[�W��ǂ�ł��邹�����C���ɂ���T�u���j���[���\������Ă��܂���D���ۂɂ́C���̒l1�C���̒l2�C���̒l3�C���̒l4(�������)�ƂȂ����Ă��܂��D
�g�їp�̃y�[�W�����Ă��������D
%�������̂ŃX�}�z���������Ɠǂ݂ɂ�����������܂���
�����m��ҁn�F�A�����肪�Ƃ��D���̃y�[�W��PC�p�̃y�[�W�Ȃ̂ŁC�X�}�z�œǂނ��Ƃ͑z�肵�Ă��܂���D�X�}�z�p�ɕύX�����Ƃ͂܂��s���Ă��܂���
���m�ʂ̕ł���̎���ɑ���n[�P���������ɂ��ā^19.09.23�n
���肪�Ƃ��������܂���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�P���������̕��͑��ɂ��ā^19.09.22�n
�ƂĂ����J�ŕ�����₷���ł�!
�w�Z�̋��ȏ���蕪����₷���ł��B
���̌`�̖�������Ή��������ł�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������̉��̌����ɂ��ā^19.09.21�n
�Z��✕�킩��Ȃ��̂őI����ɂ��ė~�����ł�
�����m��ҁn�F�A�����肪�Ƃ��D�I����ɂȂ��Ă��܂��D�I�������N���b�N���Ă��������D
���m�ʂ̕ł���̎���ɑ���n[�A���������i�����@�̂₳�������j�ɂ��ā^19.09.21�n
�����M�T�C�g�ŕ������Ă��������Ă���Љ�l�ł��B
���̊��Ⴂ�ł������ϐ\����Ȃ��̂ł����A�{�y�[�W���́y���Q�z(1)�̉����Ɛ������Ă��Ȃ��悤�Ɏv���܂��B��̓I�ɂ͘A���������̂Q�߂����ł�2x+2y=9�ł���̂ɑ��āA�ł�x+2y=9�ƂȂ��Ă���܂��B
���萔�����������܂����A�C�����Ă���������ƍK�r�ł��B��낵�����肢�������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�Q��ƂR��4(�������)�ɂ��ā^19.09.20�n
��ς����b�ɂȂ��Ă���܂��B
(-3)^3-2*3�̉����A-33�ɂȂ��Ă��܂��B
�i���̖��������āA���̑g�ݍ��킹���c��܂��B�����ɗ��҂�I��A�����ɂȂ�܂����j
������3���Ǝv���̂ł����A�������ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D(-3)^3-2*3=-27-6=-33�ł��D3���Ǝv���̂́C(-3)^2-2*3�Ɠǂ�ł��邩��ł��傤
���m�ʂ̕ł���̎���ɑ���n[�Q�_�Ԃ̋����̌����ɂ��ā^19.09.19�n
��������������₷�������]^�`�i�����x�j
����ŕ��V���[...���܂���`���邷��
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����̕ό`�ɂ��ā^19.09.17�n
�ƂĂ�������₷���A�����̕ό`��������悤�ɂȂ�܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�P���������̉������ɂ��ā^19.09.16�n
�����ė~�����Ƃ��낪�ڂ��ĂȂ�����
�����m��ҁn�F�A�����肪�Ƃ��D�����ė~�����Ƃ��낪�ǂ�ȂƂ��납�q�ׂȂ���...�ǂ�Ȍ������ŁC�����C�ǂ̌����T�C�g���璲�ׂ悤�Ƃ����̂��C����łق������̂��o�Ȃ������Ƃ������Ƃ́C�����Z�p�̖��ł�
���m�ʂ̕ł���̎���ɑ���n[�������������ƂȂ邎�̒l�ɂ��ā^19.09.15�n
�ȒP������
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�H�����̔Z�x�ɂ��ā^19.09.15�n
����� ���̋ɁA���������������Ȃ����B
(1)�@
10(%) �̐H���� 300(g) �ƁCx(%) �̐H���� 450(g) ���������Ƃ��C7(%) �̐H�����ɂȂ�܂��D
�̉�����̂P�s�ځA�u�������H���̏d���̍��v�� 300�~0.10+450�~x�~0.01(g)�v�̍Ō�̕����w0.01(g)�x�����̐�����\���Ă���̂������ł��܂���B�������肢�܂��B
�����m��ҁn�F�A�����肪�Ƃ��D10(%) �̐H���� 300(g)�Ɋ܂܂��H���̏d����300�~0.10(g)�Cx(%) �̐H���� 450(g)�Ɋ܂܂��H���̏d����450�~x�~0.01(g)�C�u�������H���̏d���̍��v�� 300�~0.10+450�~x�~0.01(g)�v�Ƃ����ꍇ�Ɋ���(�@)���͏d���̒P�ʂł��D
�@�����Ȋ��z�Ƃ��āC���̎���́u���蓾�Ȃ�����v�ł��D�Ǘ��l�����w�Z2�N���̍��ɁC�u�d���͉�(g)�ł����v�Ƃ������ɑ��āC10�Ɠ�������~�ŁC10(g)���������Ƃ����搶�������D�v����ɏo��҂Ɖ҂̊ԂŁC����̌`�Ɖ̌`�̖��ł��Ă��邩�Ƃ������Ƃ��ȁD���w�Z2�N���ŁC��(g)�ł����Ƃ������ɑ��āC���m�̐����u���v�������Ă��ɂ͂Ȃ�Ȃ��Ƃ������Ƃ͂Ȃ������悤�����D�u�c�u�c
�Ȃ��CiPhone�œǂނ̂Ȃ�g�єł̃y�[�W��ǂ�ł�������
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝�ɂ��ā^19.09.14�n
�̓_�ł���Ƃ����Ƃ��낪���ɂ��̃T�C�g�̗��_���Ǝv���܂��B���ꂩ��͖�萔�Ȃǂ𑝂₵�Ă��ꂽ��X�ɂ����T�C�g�ɂȂ�Ǝv���܂���❗
�����m��ҁn�F�A�����肪�Ƃ��D���̃y�[�W��10���y�[�W������̓��̏��߂̃y�[�W�ł��Dandroid�̋�����ʂł͕\������Ȃ���������܂��C�T�u���j���[�Ɍ�̃y�[�W���\������Ă��܂��̂ł����������Ă��������D�i�g�єł̃y�[�W�����Ă��������j
���m�ʂ̕ł���̎���ɑ���n[�ω��̊����ɂ��ā^19.09.12�n
y=14x+3
x���R����V�ɑ��������Ƃ��̕ω��̊����́H�Ȃ�ł��������Ă�������
�����m��ҁn�F�A�����肪�Ƃ��D���̃y�[�W��ǂ�ł��̎��₪����̂͂��������ȂƁH�����ƁC���Ȃ��͂��̃y�[�W��1�����ǂ�ł��Ȃ��悤�ł��D�ǂ�ł��玿�₵�Ă��������D
���m�ʂ̕ł���̎���ɑ���n[�H�����̔Z�x�ɂ��ā^19.09.08�n
�H�����̔Z�x�̖��͋�肾�����̂ł����A�u�����^���v�̖��Ȃǂ������Ď��g�݂₷���`���������̂ŁA�l�I�ɔ��ɂ��₷�������ł��B���P�_�͎��Ƃ��Ă͓��ɂȂ��悤�Ɋ����܂����B���肪�Ƃ��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Q���������̉������i�܂Ƃ߁j�ɂ��ā^19.09.08�n
�ƂĂ��킩��₷�������ł��I�I
�����m��ҁn�F�A�����肪�Ƃ��D
��?/�P�邳��/19.09.07
Google�Ōv�Z�̎d���ƒ��ׂĂ����炱�̃T�C�g���o�Ă�������
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�ω��̊����ɂ��ā^19.09.04�n
�u���@�����@����v����3�����̋L���ɂ͂����āA�ƂĂ��ǂ������ł��I
�w�Z�Ŏ��Ƃ��Ă�Ƃ��͉��������Ă���̂����悭������Ȃ��āA�`���v���J���v���̏�Ԃ��炱�̋L����ǂ̂ł����A�ƂĂ�������₷���A�ǂ������ł��B
�������Ŗ����S����ł��āA���X�ł�😁
�����ω��̊����̖�肪���������Ǝv���܂��B
�������������ʂ����߂��肪�����������ł��c�B
�����m��ҁn�F�A�����肪�Ƃ��D�u�����ʂ�������Ȃ���C�ω��̊����͕�����Ȃ��D�v�u�ω��̊������������Ă���C�����ʂ��������Ă���D�v�Ƃ�����̂ŁC�����ʂ��͕ω��̊�������ʖڕW�ɂȂ�܂��D�����ŁC�ω��̊������e�X�g����C�����ʂ��������Ă��邩�ǂ������e�X�g�ł���̂ł��D
���m�ʂ̕ł���̎���ɑ���n[��������4�ɂ��ā^19.09.03�n
�|�P�@��a�Ƃ��A�|�P�Q��ςƂ���Ƃ��A�����o������̐����́A�R�Ɓ|�S�ł��锤�ł��B
���A���́u�����̑��v�ł̓o�c�Ƃ������Ă��܂��܂��A���̂ł��傤�H
�����m��ҁn�F�A�����肪�Ƃ��D�{���C���l�œ�������̂́C���p�����œ����Ȃ���Ȃ�܂���D�i�������œ����Ă����߂ł��傤�j
�@�������C���ɂ͑S�p�����ŕ��C�ʼn��Ă���l�����܂��D�A���r�A������S�p�ɂ������̂ɂ��ẮC�G���[�����Ƃ��ċ��e�͈͂ɂ��Ă��܂����C���Ȃ��̏ꍇ�́C�}�C�i�X�̕������C�[�C��C�\�C�P�C�Q�ȂNJ����́u�����v�C�A���_�[�o�[�C�Ȃǃ}�C�i�X�ȊO�̑S�p�����œ��͂��Ă���\��������܂��D���̉\���Ƃ��ẮC2�Ԃ̖��Ȃ̂�3�Ԃ̍̓_�{�^���������Ă���ꍇ������܂��D
���m�ʂ̕ł���̎���ɑ���n[�u���������v�̂͂������ɂ��ā^19.08.31�n
�����Ă�̂�������Ȃ��A�C�R��������܂��B
���U�Ƒ��̏��ŊԈႦ�ā@�A�C�R�����m�F���Ȃ��Ƃ����Ȃ��̂�
������₷���A�C�R�����g���Ă���������Ɗ������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�J�Ɛ���̈Ⴂ�͕�����ł��傤
���m�ʂ̕ł���̎���ɑ���n[�������������ƂȂ邎�̒l�ɂ��ā^19.08.31�n
����Ɨ����ł��܂���
�ƂĂ��킩��₷�������ł�(�@�E�ցE)�t���t��
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�A���������̉������i����@�j�ɂ��ā^19.08.30�n
��Q�͉��̏オy �ʼn���x�Ȃ̂ł����H
�����m��ҁn�F�A�����肪�Ƃ��D����̈Ӗ����ʂ��܂���D��Ƃ����Ƃ����l�����Ŗ��������Ă���̂ł����H��Ƃ͉��̂��Ƃł����H
���m�ʂ̕ł���̎���ɑ���n[�H�����̔Z�x�ɂ��ā^19.08.22�n
��萔�������āA
��育����������܂����B
������ׂ��������Ă���A
�ƂĂ����ɗ����܂���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�P���������̉������ɂ��ā^19.08.19�n
10-3X-8-4X
�����m��ҁn�F�A�����肪�Ƃ��D�����́C1���������̃y�[�W�ł��D1���������łȂ����̂������āC�ǂ����Ăق����̂��������ĂȂ��H���ꂪ1���������ł͂Ȃ��Ƃ������Ƃ͕������Ă��܂����H
���m�ʂ̕ł���̎���ɑ���n[�_�Ώ̂Ȑ}�`�ɂ��ā^19.08.18�n
�S�R�킩���
�����m��ҁn�F�A�����肪�Ƃ��D�f������ɕs���������Ă��Ă��C������i�݂܂���D������悤�ɂ��邽�߂ɂ́C�����悢���ƍl���邱�Ƃ��d�v
���m�ʂ̕ł���̎���ɑ���n[�~�ɓ��ڂ���l�p�`�ɂ��ā^19.08.18�n
���w���̓��e�͖Y��Ă��܂��Ă����̂ŏm�̗̍p��������O�ɉ����Ă݂܂����B������₷�������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���������mhuruimonoto����n[�ɂ��ā^19.08.17�n
���̖��͒��앨�ł���
���앨�ł͂Ȃ���������Ăق���
�����m��ҁn�F�A�����肪�Ƃ��D���w�������̂悤�Ȋϓ_�Ŏ��₷�邱�ƂɊ��S���܂���
�@���{�̓x���k���������Ȃ̂ŁC���쌠�̐����ɂ͊������ւ̓͂��o�Ȃǂ̗l���͕s�v�ŁC�c���ł����w���ł��C�앶1���C�G��1���������Ă��C�������u�Ԃ��璘�앨�Ƃ��Ē��쌠���F�߂��܂��D������C�����ꂽ���̂Œ��앨�łȂ����̂�T����������ł��D�������C���̂悤�Ȃ��̂́C���쌠���F�߂��܂���D���x��J�ʂ̂悤�ȃf�[�^�C���w�╨���̒藝�C�p�����{��̒P��╶�@�D
�@�����ŁC�����ȂƂ���ɗ���̂��C�Q�l���C�����C���w�̖��W�̂悤�Ȃ��̂ł��D�ʂ̖��C���Ƃ��C1+2=3�̂悤�ȊȒP�Ȍv�Z���ɂ͒��쌠�͔F�߂��܂��C�������w�K���₷���`�ŕ��ׂĖ��W�ɂ������́C�w�������Ď����̌`�ɂ������̂Ȃǂ́C�ʂ̓��e�ɑ��ĂłȂ��C�ҏW���Ƃ��Ē��쌠���F�߂��܂��D�܂��C�������ł������ȍH�v�����Ă����āC�ގ��i���߂����Ɍ�������Ȃ����̂ɂ́C���쌠���F�߂���ł��傤�D�Q�l���ł��C�Ǝ��ɍH�v����������╪����Ղ��C���X�g�ɂ͔F�߂��₷���X��������ł��傤�D
�@�Ƃ���ŁC���Ȃ��͉��̂��߂Ɂu���앨�ł͂Ȃ���������Ăق����v�ƍl���Ă���̂ł����H���l�̒��앨�ł��C�����������ɓ��ĂƂ��ď�����ł́C�����͂���܂���D��������̂́C�u���l�̒��앨�Ȃ̂Ɏ����̒��앨�Ƃ��Č��\����v�悤�ȏꍇ�ł��D
���m�ʂ̕ł���̎���ɑ���n[�����̕ό`�ɂ��ā^19.08.17�n
������킩��Â炢�ł�m(_ _)m
�����m��ҁn�F�A�����肪�Ƃ��D�g�єł͕ʃy�[�W�Ə����Ă�����
���m�ʂ̕ł���̎���ɑ���n[���Ώ̂Ȑ}�`�ɂ��ā^19.08.15�n
��������
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�A���������̉������i����@�j�ɂ��ā^19.08.15�n
�}�C�i�X�ƃv���X�̕��z�@���̎��ɂǂ����炪�D�悳��邩���܂��ɕs���ł��B
�ǂ�������A�����ł��܂����H
�����m��ҁn�F�A�����肪�Ƃ��D�A���������̑���@�̋��ނ̒��ŁC���z�@���Ƃ��D��Ƃ����p�ꂪ�ǂ������W�Ŏ��₳��Ă���̂��C�S���ʂ��܂���D�����Ƌ�̓I�Ȗ��������Ď��₵�Ă��������D���z�@���ƗD��͊W�Ȃ��̂ł͂Ȃ��̂��H
���m�ʂ̕ł���̎���ɑ���n[�P���������̉������ɂ��ā^19.08.15�n
�[9y�[y�Ȃǂ̂�肩���Ȃǂ̂��Ăق���
�����m��ҁn�F�A�����肪�Ƃ��D1���������̉������̃y�[�W�ŁC�u�[9y�[y�Ȃǂ̂�肩���v������\���Ă���̂������ł��܂��C���ލ����ȒP�ɂ���v�Z�Ȃ�,
���̃y�[�W�Ȃǂ����Ă�������
�{���ɂ킩��₷�������ł��B
�\�K�ɖ𗧂��܂��I
�ł����A180�x�[72�x�́[���������Ă��܂��B
���肪�Ƃ��������܂�😊
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[2��ƂR���ɂ��ā^19.08.14�n
�킩���
�����m��ҁn�F�A�����肪�Ƃ��D��������I��肾�D�ł���悤�ɂȂ邽�߂ɂ́I�Ɩ��_���i���āC�����Ȗ�肩���������̂ł��D
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝�ɂ��ā^19.08.13�n
���͊m�F�ɂȂ��ĂƂĂ��ǂ������̂ł����A�����͏�������������ɂ��Ă��ꂽ��ǂ������ȂƂ����܂����B
�����m��ҁn�F�A�����肪�Ƃ��D��{�̃y�[�W�ɂ͊�{�������Ă���C���p�̃y�[�W�ɂ͉��p�������Ă���܂��D�ڎ������ǂ��Ă��������D
���m�ʂ̕ł���̎���ɑ���n[A=B=C�^�̘A���������ɂ��ā^19.08.11�n
A=B=C=D�^�̕�������
A=B
A=C
A=D
�̂悤�ɂ��ĂƂ��Ă���������ł����H
�����m��ҁn�F�A�����肪�Ƃ��D����ł����ł��D���ɂ��CA=B, B=C, C=D�Ƃ��Ă��悢�D
�@�������C���w�Z�ł͂����������͏o�܂���D�Ȃ����Ƃ����ƁC��������3����A���������́C���m����3�̂Ƃ��ɂ��܂������܂�(*1)���C���w�Z�̘A���������͖��m����2�Ȃ̂ŁC��������3�ɂȂ�ƕ��ʂ͉����Ȃ�(*2)
8��2(2+2)�͂ǂ�����ĉ����Ηǂ��ł����H
�����m��ҁn�F�A�����肪�Ƃ��D���܂�悢���łȂ��C�q�������点�邽�߂̃g���b�N�̂悤�Ȃ��̂Ȃ̂ŁC��������Ƃ悢�D
�@�ڂ��������ƁC2�~4�̂悤�Ȍv�Z�ɂ��āC2�̐����|����O�������ł́u�|���Z�v�Ƃ������Ƃɂ���Ɗ|���Z��2�̐��̊Ԃ̉��Z�Ƃ��Č��߂��܂��D����2�~4=8�̂悤�Ɋ|���Z���������ʂ̐��������ł́u�ρv�Ƃ������Ƃɂ��܂��D���̂Ƃ��C���w�P�N���ŕK���o���Ȃ���Ȃ�Ȃ����Ƃ́C���̂Q�̎��̈Ⴂ�ł��D

�̂悤��2�~4���܂�1�̐��ɂȂ��Ă��炸�C�u�|���Z�v�ɂȂ��Ă���ꍇ�́C2��8�Ɛ�Ɍ������܂��D

����ɑ��āC

�̂Ƃ��ɁC

�̂悤�Ɋ|���Z�̌��ʂ��~���g��Ȃ��u�ρv�̌`�ŏ�����Ă���Ƃ��́C

�͂P�̐�

��\���܂��̂ŁC

�ɂȂ�܂��D
�ȏ�̓��e�͏d�v�Ȃ̂ŋL���ɗ��߂�l�ł�������܂����C�ȉ��̓��e�͐��w�̉����̘b�ł͂���܂���D
�Q�̐��̐ςɂ��ẮC�~�̋L���͏ȗ��ł��Ȃ��̂�

��

�ł͂Ȃ�

��

�ł͂Ȃ��D
���������t���Ă���Ƃ���
&chf=bg,s,fff9f9)
�Ə����C

�̂��Ƃ��낤�ȂƑz���͕t�����C���ꂪ�|���Z��\���Ă���̂��ς�\���Ă���̂��C���܂��Ă���킯�ł͂Ȃ�����C
&chf=bg,s,fff9f9)
��

��\�����C

��\�������܂��Ă��Ȃ��D��������
&chf=bg,s,fff9f9)
�̋L�����C���w�Z�ŏK�����w�̋L���̖ɉ����Ă��Ȃ����Ƃ������ł��D
���ȏ��ł��������菭�����x���A�b�v�������ŁA�ԈႦ�����ɂȂ����肵�����NJy�����������Ƃ��o�����̂ŁA��ϗǂ����K���o�������������Ă悩�����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������g�������ɂ��ā^19.08.08�n
X�������̂Ƃ��A���̎��́c���Ă������ŕ�����Ȃ��̂�����܂��B
�����m��ҁn�F�A�����肪�Ƃ��D����̎d�����悭�Ȃ��ł�.���̃y�[�W�ɂ�X�������̂Ƃ��Ƃ����`�̕��͂͂���܂���D���ނ̊Ǘ��l�i���j�������ǂނƁC�u�Y�ݎ�������̂ł��v�Ƃ��������ȂƂ炦�ǂ���̂Ȃ��b�ɕ�������̂ł��D����Ƃ��C�ǂ����̋��ȏ��Ƃ��h��ɂ��̂悤�ɏ����Ă���̂ł����H
�@���e���猾���C�u���̒l�v�Ƃ������ڂ̘b�̂悤�ł��̂ŁC
���̃y�[�W����C�扽�₪������Ȃ��Ƃ�����ɖ�����肵�Ď��₵�Ă��������D
�����ȊO�͂悭�킩��܂����B
���肪�Ƃ��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D�����͂��炢�ł����H���������ӂɂȂ�ƁC�����̐��w�͂��Ȃ�y�ɂȂ�܂��D
���m�ʂ̕ł���̎���ɑ���n[��`�̖ʐρC�~���̕\�ʐ��ɂ��ā^19.08.05�n
��`�̒��S�p��������Ȃ��Ƃ��͑��ʐς͂ǂ̂悤�ɋ��߂�����ł����H
�����m��ҁn�F�A�����肪�Ƃ��D��`�̒��S�p��������Ȃ��Ƃ��́C��`�̒��S�p�����߂Ă���v�Z���܂��D���̃y�[�W��
�P�O�̃y�[�W�ɂ��̗��K������܂��D
�@���S�p�������ĂȂ��Ƃ��́C�~���ɂȂ��Ă��Ē�ʂ̔��a(r)��������Ƃ��C��`�̌�(L)�̒�����������Ȃǂ̍ޗ����ʂɎ�����܂��D������g���Ē��S�p�����߂܂�
�ƂĂ��킩��₷���ĎQ�l�ɂȂ�܂����I
�ڂ��Ă������������̂����̌X�������ꎟ���Őg�߂Ȃ��̂������Ă������������ȂƎv���܂����B
�ƂĂ�����ł�������Ƃ���낵�����肢���܂��I
�����m��ҁn�F�A�����肪�Ƃ��D
���̃y�[�W�́u�˂̒����v���C�u�d��̂����W�v�Ƃ���C����−x−5�ɂȂ��
x %�Z�x�̐H����1�O�������ɗn���Ă���H���̗�(%)�̓����������Ă������������ł�
�����m��ҁn�F�A�����肪�Ƃ��D�]�T������Ύ���ɂ͓����܂����C���ꓚ�I�ɒ����Ă���ƁC��肪�ς��C�܂��ʂ̎�������Ȃ���Ȃ�Ȃ��Ȃ�C�͂��t���܂���D�u�l�����v��g�ɒ�����悤�ɂ��āC��肪�ς���Ă���������悤�ɂ��܂��傤�D
���̃y�[�W������
�@�܂���肪�Ԉ���Ă��܂��̂ŁC���̂悤�ɕς��܂��D�ux %�Z�x�̐H����1�O�������ɗn���Ă���H���̗�(g)�v←�������Ȃ���C��蕶�ɓ����ix %�j�������Ă��邱�ƂɂȂ�C��肪���藧���Ȃ��D
�@���̖��̓����F0.01x
�@����ł́C1 %�Z�x�̐H����x�O�������ɗn���Ă���H���̗�(%)�́H
��������͂��āA�̓_����������Ă��A�������ǂ����킩��܂���B
�����m��ҁn�F�A�����肪�Ƃ��D���̃y�[�W�̐擪�Ɂu�g�єł͕ʕŁv�Ə����Ă��܂��̂ŁCandroid�̋�����ʂŌ���Ƃ��́C�g�єł̕������Ă�������
���m�ʂ̕ł���̎���ɑ���n[�Q�����̃O���t�ƒ����Ƃłł���}�`�̖ʐ��ɂ��ā^19.08.01�n
�������ƒ������ʐ�1�́A�����̕��������ƕ�������A�����Z�ɂȂ�A
�������ƒ������ʐ�2�́A�����̕��������Ɛ��╉�ƕ�������A�����Z�ɂȂ�A
�Ƃ������ƁH
�����m��ҁn�F�A�����肪�Ƃ��D�e�������S�̘_���Ƃ��Ăǂ̂悤�ɔ[�����邩�͎��R�ł����C�����Ƃ��Ắu��Ӂv���u�����v�����̐��Ōv�Z���Ĉ����Z�ɂ��܂��D
���m�ʂ̕ł���̎���ɑ���n[�i���o�[�v���C�X�̖���ɂ��ā^19.08.01�n
�ԈႢ���Ԃ��Ȃ��Ă�C������A�C�̏��ׂ�������܂�����͎����Ƃ����ꍇ�d��Ȍ��ׂł�
�����m��ҁn�F�A�����肪�Ƃ��D�ԈႢ��ԂŎ����ƕ�����₷���Ă����ˁD���܂�傰���ȕ\���͔����������悢�ł��傤�D
���m�ʂ̕ł���̎���ɑ���n[�A���������̉������i����@�j�ɂ��ā^19.07.30�n
�撣��܂��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�f���������̉��p�ɂ��ā^19.07.30�n
���w���̖��ɑf���������������邽�߂Ɋ��p�������܂����B���������̎���荡�̂ق����������ł��A�܂��܂����ɂ͕������Ȃ��ƕ��ł��܂����B���肪�Ƃ��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D����������b�̗́i←���ԓ��̌������j�̂�����ɂ́C�]�����悢�悤�ł�
���m�ʂ̕ł���̎���ɑ���n[�Ή��\�ɂ��ā^19.07.26�n
y=x2+2
�����m��ҁn�F�A�����肪�Ƃ��D���w�Z�ɂ͂����������͂���܂���D���Z���Ȃ獂�Z�̖������Ă��������D
���m�ʂ̕ł���̎���ɑ���n[�_�Ώ̂Ȑ}�`�ɂ��ā^19.07.23�n
�s�����̍ۂɂǂꂪ�s�����Ȃ̂�����Ȃ������B
�����m��ҁn�F�A�����肪�Ƃ��D�I����Ȃ̂ŁC2�C3��������̂ŁC�����牽�܂őS�������Ă��܂��ƁC���k�̍l����͂��ǂ��Ȃ�̂��Ǝv���܂����C�т����肷��悤�Ȏv���Ⴂ��M������ł���ꍇ�ɂ͍���Ȃ���������Ȃ��̂ŁC�ꉞ���o��悤�ɂ��܂����D���ꂪ�ǂ����Ƃ��������Ƃ�������
����t���m�}�~ �C�`�m�Z����^19.07.22�n
������Ȃ���肪����̂ʼn������������ĉ������B
���肢�v���܂��B���͈ȉ��̒ʂ�ł��B
�i7X�|11�j�F�i5X�{11�j���Q�F�R�@�@X�̉��A���肢�v���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D���w�Z�̗��V�Łu�����̐ς͊O���̐ςɓ������v�Ƃ����̂��g���̂��ȒP�ł��傤�D
�i7X�|11�j�F�i5X�{11�j���Q�F�R→2(5X+11)=3(7X-11)→10x+22=21X-33→11X=55→X=5
���m�ʂ̕ł���̎���ɑ���n[�ω��̊����ɂ��ā^19.07.18�n
�i10�j�̖�蕶�́ux���v�|4����|1�܂ő�������A�Ƃ�������x����ꂽ�ق���������₷�������B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�����̕ό`�ɂ��ā^19.07.16�n
�w���v�����łȂ��u�v�ȂǂƂ����悤��
�������ڂ��ė~�����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�{�^���̃��x����HELP�ł����C�܂ŏ����Ă���܂�
���m�ʂ̕ł���̎���ɑ���n[ ���P.�������̉���Ɨ��K�ɂ��ā^19.07.16�n
�����{�T�C�g�ɂ͑�ς����b�ɂȂ��Ă���A���肪�Ƃ��������܂��B
���4�̉E�ӍŌ��x���^�C�v�~�X���Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D��蕶�ɗ]�v�Ȃ����t���Ă���Ƃ������ƂŁC�폜���܂���
���m�ʂ̕ł���̎���ɑ���n[�������̕\�����ɂ��ā^19.07.09�n
���U�̂S�ԉ�����݂��番�q�́|3ab�~b2�@��a ���������݂�Ɩ����Ȃ��Ă��܂��A�Ȃ��ł����H
�����m��ҁn�F�A�����肪�Ƃ��D�ŏ����܂��D�����Ȏ�������Ă���悤�ł����C���̎��₪�o��̂́u�h�����v���x���̊ȒP�ȗ��K���ł��Ă��Ȃ����炾�ƍl�����܂��D
���m�ʂ̕ł���̎���ɑ���n[�~�ɓ��ڂ���l�p�`�ɂ��ā^19.07.06�n
�w�Z�̕��K�Ƃ��Ďg�킹�Ă��������܂����B���J�Ȑ����ƖL�x�Ȗ��ŕ��ɂȂ�܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����i�S����,����,�����j�ɂ��ā^19.07.06�n
���܂��܌������̂����ǁA�ƂĂ��M�d�ȓ��e���ȂƊ����܂��B����������̂ŁA�y�����w��ł���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������̉��̌����ɂ��ā^19.07.04�n
�}�C�i�X�Ȃǂ̋L���͑S�ēǂݎ���悤�ɂ��ė~����
�����m��ҁn�F�A�����肪�Ƃ��D�v�]�̈Ӗ����ʂ��܂���...iPad���c�Ɏg���ƕ������ǂݎ��Ȃ��Ƃ������ƂȂ̂��H
���m�ʂ̕ł���̎���ɑ���n[����ɂ��ā^19.07.02�n
�T�C�g�̕��͋C�𖾂邭���Ăق���
�����m��ҁn�F�A�����肪�Ƃ��D�v�]�ɉ�����͖̂����ł��D���邢�Ƃ͂ǂ��������ƂȂ̂���������Ȃ��i�È��j������Ă���j�D�y�[�W�������߂���D
���m�ʂ̕ł���̎���ɑ���n[�ő���ƍŏ����{���ɂ��ā^19.06.26�n
�����I�I�I�I�킩��₷���čō��ł��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������������ƂȂ邎�̒l�ɂ��ā^19.06.25�n
���ɓ���܂����B
�����m��ҁn�F�A�����肪�Ƃ��D�ǂ��炩�Ƃ����C������̖��ł�
���m�ʂ̕ł���̎���ɑ���n[���Ώ̂Ȑ}�`�ɂ��ā^19.06.24�n
�悭����₷�����͂�����
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�A���������ɂ��ā^19.06.24�n
�ƂĂ�������₷������ł����B
�����₷�� �ԈႢ��������₷�������ł��B
����������Ăق����ł�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�A���������ɂ��ā^19.06.23�n
3x�S��=�P
5x➖�V��=2
�����m��ҁn�F�A�����肪�Ƃ��D����Ȃ̂��C�ԈႢ�̎w�E�Ȃ̂��C���t���g���ĕ\�����Ȃ��ƈӖ����ʂ��܂���D3x�S��=�P
5x➖�V��=2�Ƃ����A���������͒��w�Z�ł͈����܂���D�����C3x+�S��=�P,5x−�V��=2�Ƃ����A���������ł�����C���̃y�[�W�̉��[�ɕt�^������܂��̂ŁC�����ɐ������������߂C�������o�܂��D�i�����ɂȂ�܂��j
���m�ʂ̕ł���̎���ɑ���n[�������g�������ɂ��ā^19.06.23�n
�ō��ɂ����T�C�g���Ǝv���܂�
�ł��A���w��1~6���w��1~3���Z1~3�ɑΉ������肷�ׂďo���Ă��ꂽ�炠�肪�����ł�
�����m��ҁn�F�A�����肪�Ƃ��D���w���ɂ͋����Ă��܂���D
?�m?�^19.06.23�n
3�ӂ̒������^�����Ă���O�p�`�̍������O�����̒藝�ŋ��߂鎞�ɁA�ǂ����x�ƒu���Ȃ�������Ȃ��ƌ��܂��Ă����ł����H
�����m��ҁn�F�A�����肪�Ƃ��D�ǂ̕ӂ�x�Ƃ�����,���������͂���܂���Dy�ł��悢,a�ł��悢�D�����͂�����̎��R���I
���m�ʂ̕ł���̎���ɑ���n[�O�ӂ̒������^����ꂽ�O�p�`�ɂ��ā^19.06.23�n
�Ȃ��BH��x�Ƃ����ł����H
�����m��ҁn�F�A�����肪�Ƃ��D�ǂ̕ӂ�x�Ƃ�����,���������͂���܂���Dy�ł��悢,a�ł��悢�D�����͂�����̎��R���I
���m�ʂ̕ł���̎���ɑ���n[�����Ǝ� �i�}�`�j�ɂ��ā^19.06.23�n
�Q�l�̕����̓��e���������܂��H
�����m��ҁn�F�A�����肪�Ƃ��D���̃y�[�W�͉���̂[�W�ł͂Ȃ��C�����Q�[���ɂ������̂ł��D�����
���̃y�[�W�ɂ���܂�
�߂����Ⴂ���I
���̌`���̃Q�[���̂悤�Ȃ̂�������������Ƃ���
�����m��ҁn�F�A�����肪�Ƃ��D���̋��ނ����n�߂����߂̍��i20�N�قǑO�j�ɂ́C�l�X�Ȍ`���̃Q�[���I�Ȃ��̂𑝂₵�Ă��܂������C�ǎ҂�����銴�z����́C�����������ȏ��������Ă��Ȃ��C���ȏ���������Ȃ����x���̎��₪�����̂ŁC�ŋ߂͒n���悤�Ȋ�{�̉���ɗ͂����Ă��܂��D
���Ȃ��̊��z�́C�M�҂������\�z�����悤�ȁC�ǂ��炩�Ƃ����u���������ł���`�[���́v���z�̂悤�ł��D
���m�ʂ̕ł���̎���ɑ���n[�_�Ώ̂Ȑ}�`�ɂ��ā^19.06.22�n
������₷�������ŁA����4�̖�肪�ǂ������ł��B���肪�Ƃ��������܂��I😍
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������Q����Ƃ��̎��̒l�ɂ��ā^19.06.19�n
�����A�傫�����Ă�������
�����m��ҁn�F�A�����肪�Ƃ��DCtrl+ �i�R���g���[���L�[�������Ă���ԂɃv���X�L�[�������܂��j
���m�ʂ̕ł���̎���ɑ���n[�������̉������ɂ��ā^19.06.18�n
�E�ƌP���̎������Ɋ��p�v���܂����B���̂悤�ȗL�p�ȃR���e���c���Œ��Ē����Ă��肪�����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�P���������̉������ɂ��ā^19.06.17�n
���ȏ������ӂɂȂ����I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[1�����ɂ��ā^19.06.16�n
�ƂĂ�������₷���ł��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[2��ƂR��̕����ɂ��ā^19.06.16�n
��������Ă��āA�������킩��₷���Ă悩�����B
�܂����ȂƂ�������̖�������Ăł���悤�ɂȂ����B�����Ď������ł��Ȃ��Ƃ����O��I�ɂ��A�e�X�g�ł��ł���悤�ɂȂ肽���Ǝv�����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���l���E�X�̒藝,�`�F�o�̒藝�ɂ��ā^19.06.04�n
�E�`�F�o�̒藝�̏ؖ�
�i��j
��RTA�䁢RBQ������
�i���j
��RTA�䁢RBC������
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[�A���������ɂ��ā^19.06.03�n
������
�����m��ҁn�F�A�����肪�Ƃ��D���z���Z�����ĉ������Ȃ�
���m�ʂ̕ł���̎���ɑ���n[�����ŕ\���ꂽ���̑召��r�ɂ��ā^19.06.02�n
�ƂĂ�����
�����m��ҁn�F�A�����肪�Ƃ��D���z���Z�����ĉ������Ȃ�
���m�ʂ̕ł���̎���ɑ���n[��@�̌����ɂ��ā^19.06.01�n
(1/a+b)^2�͂ǂ��Ȃ�H
�����m��ҁn�F�A�����肪�Ƃ��D���̃y�[�W�͒��w�������̃y�[�W�ł��D���w�̐��w�ɂ͕������͂���܂���D������e��L���̊������獂�Z�������̕��̂悤�ł����C��������
���̃y�[�W�Ȃ�
�X�����[���̏ꍇ�͂ǂ�ȃO���t�ɂȂ��ł���
�����m��ҁn�F�A�����肪�Ƃ��D
���̃y�[�W�̗�9�ɏ����Ă��܂����C�����ɕ��s�Ȓ����ɂȂ�܂�
�_�Ώ̂łȂ��}�`�́A�Ȃ�ƌĂт܂����H
�����m��ҁn�F�A�����肪�Ƃ��D���ɓ��ʂȖ��O�͂Ȃ��ł��傤�D�P�ɁC�_�Ώ̂łȂ��}�`�ƌĂԂ����ł��傤�D
���m�ʂ̕ł���̎���ɑ���n[�ڌ��藝�ɂ��ā^19.05.25�n
�ƂĂ��킩��₷�������ł��A���肪�Ƃ��������܂�
����e�X�g�A������܂���(*^��^*)
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������Q����Ƃ��̎��̒l�ɂ��ā^19.05.23�n
�ƂĂ��킩��₷���������Ȃ̂ł����A�����������������Ȃ����Ăł��Ȃ���Ώc�ɒ��������Ă��������ƍK���ł�
�����m��ҁn�F�A�����肪�Ƃ��DiPad���c�Ɏg���Ă�����悤�ł����C��ԍŏ��̏��Ɂu�g�єł͕ʕŁv�Ƃ����Ă���܂��̂ŁC�������
���m�ʂ̕ł���̎���ɑ���n[���������P�ɂ��ā^19.05.21�n
�ƂĂ��ǂ��ł��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������ɂ������ɂ��ā^19.05.19�n
�ƂĂ��킩��₷���ėǂ��ł��I
�܂��A���p���܂�😁
�킩�肸�炢
�����m��ҁn�F�A�����肪�Ƃ��D��l�̐l����1���ȓ��ɑ������銴�z���������...��ւƕ֔�Ƃ�����������Ǐ�̗����Ɍ�������́H�݂����ȁi�͖k����ɗ��݂܂���j
���m�ʂ̕ł���̎���ɑ���n[�����̕ό`�ɂ��ā^19.05.16�n
2a��b(a)
�����m��ҁn�F�A�����肪�Ƃ��D���ꂪ�ǂ������܂������H����ł����C�ӌ��ł����C�����ǂ����Ăق����̂ł����H����ł́C�ʂ肪����̂�������ɁC�������Ȃ��ɁC����𓊂����Ă���悤�Ȃ��̂ł��D
���m�ʂ̕ł���̎���ɑ���n[�P���������̉������ɂ��ā^19.05.16�n
�n���ɂ͂������肷���ē��
�����m��ҁn�F�A�����肪�Ƃ��D�����Z�̐��w�́C�������K�ɋ߂��v�f�������āC������C��������C�ǂ��������ł͐g�ɒ����Ȃ����̂���R����܂��D�ȒP�Ɍ����C�̂Ŋo����̂ł��D���̂��߂ɂ́C���������̕��ʂ����Ȃ��Ȃ��Ɛg�ɒ����Ȃ��̂ŁC����Ȃ�̕��ʂ�p�ӂ��Ă���̂ł��D
���m�ʂ̕ł���̎���ɑ���n[�W���̌����ɂ��ā^19.05.16�n
����ɂ��́@�{�Əd�˂��悤�Ǝv���܂��@�����݂�10�J�����炢�͎g���Ǝv���܂��@����܂���ˁ@�ׂɂȂ�܂�
�����m��ҁn�F�A�����肪�Ƃ��D�d�˂��悤�Ƃ����������C�\��������܂��C�ǎ҂ɂȂ��Ă����Ƃ��������͕�����܂��D
���m�ʂ̕ł���̎���ɑ���n[�����̕ό`�ɂ��ā^19.05.15�n
�ǂ��ǂ��ǂ������ł����B
�킩��₷��😄
�����m��ҁn�F�A�����肪�Ƃ��D���X�X�R�Əd�˂�̂́C�������̋_���Ղ̗V�ѐS���ڂ̑O��ՂƓ�������������
���m�ʂ̕ł���̎���ɑ���n[���Ώ̂Ȑ}�`�ɂ��ā^19.05.13�n
���Ώ̂Ȑ}�`�̏������������Ă��������Ɗ������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�ς��������ł��D���ʂ̎���́C�^����ꂽ�}�`�����Ώ̂ł��邩�C�����łȂ����̂����ꂩ�Ɛq�˂܂��D����́C���łɂ���}�`��ς����ɁC�Ώ̎��̑I�ѕ��ɂ���āC����Ƃ����E�Ƃ����ΏۂɂȂ�悤�Ȏ���I�ׂ邩�ǂ����Ƃ������ł��D
����ɑ��āC���Ώ̂Ȑ}�`�̏������ƂȂ�ƁC���ʂ�ł������Ă��ꂪ�����ł��ƌ������̂͂Ȃ��D
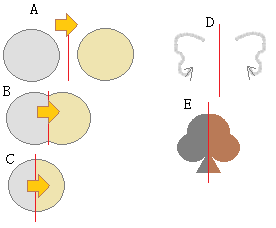
(A)�̂悤�ɑΏ̂̎������߂�ꍇ�C���̉E�ɂ͉����Ȃ��D���̍��������ɉf�����悤�ɉE�Ɉڂ��ƁC���E�S�̂łP�̐��Ώ̂Ȑ}�`�ɂȂ�D
(B)�̂悤�ɑΏ̂̎������߂�ꍇ�C���̉E�ɂ������}�`�͎̂ĂāC���̍��������ɉf�����悤�ɉE�Ɉڂ��ƁC���E�S�̂łP�̐��Ώ̂Ȑ}�`�ɂȂ�D
(C)�̂悤�ɑΏ̂̎������߂�ꍇ�C���̉E�ɂ������}�`�͎̂ĂāC���̍��������ɉf�����悤�ɉE�Ɉڂ��ƁC���E�S�̂łP�̐��Ώ̂Ȑ}�`�ɂȂ�D���̏ꍇ�C���̉E�ɂȂ������̂ƁC������ڂ��Ă������̂�����������C���̐}�`�ƕς��Ȃ��D
(D)�̂悤�ɁC�E��ƍ���ɉ��M�������āC�E��͉E�ɍ���͍��ɓ������ƁC���E�Ώ̂Ȑ}�`���`����D
(E)���̃y�[�W�̐擪�̗�̂悤�ɁC�܂莆�����Ő܂��ďd�˂Ă����Ă���C2���d�˂ăn�T�~�Ő��āC�J�����E�Ώ̂Ȑ}�`���ł���D
�������߂ɂȂ�܂��I�@�@�������ȊO�̐��w�����e���Ă�������
�����m��ҁn�F�A�����肪�Ƃ��D���j���[�ɍs����悤�ɂȂ��Ă��܂��̂ŁC���j���[�����Ă��������D
���m�ʂ̕ł���̎���ɑ���n[���W�ɂ��ā^19.05.11�n
���������ڂ��������Ă��������I
�����m��ҁn�F�A�����肪�Ƃ��D�ǂށC���������łȂ��C�������ۂɂ�钆�Őg�ɒ������Ƃ���������܂��D���ɁC���w�Z�̐��w�́C���K�I�ȗv�f�������Ǝv���܂��̂ŁC�Ȃ�ׂ���R����Ă��������D
���m�ʂ̕ł���̎���ɑ���n[�P�����Ƒ������ɂ��ā^19.05.11�n
�Ƃ��Ă����₷�������ł�‼️😀
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�ڌ��藝�ɂ��ā^19.05.10�n
��������ł�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝�ɂ��ā^19.05.08�n
�������҂ł����w����̂����炢�����Ă��܂��B���ɗ������₷�������ł��B�{�P�h�~�ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�H�����̔Z�x�ɂ��ā^19.05.07�n
(��)20���̐H����n�����ĂT%�̐H��������肽���B��������������悢���B
�݂����Ȗ��̉���Ȃ�������Ƃ����Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝�ɂ��ā^19.05.03�n
������Ȃ�����������₷��������Ă����Ă悩�����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�P�����Ƒ������ɂ��ā^19.04.30�n
X-3���̍��������Ȃ�������-3�ł����H
�����m��ҁn�F�A�����肪�Ƃ��D����3���������͂���−3���ł��D
���m�ʂ̕ł���̎���ɑ���n[�ǎҊ��z���ɂ��ā^19.04.30�n
���`�����ɂȂ��Ă���3���Ԍo���Ă��`
����ȗǂ��̂ɂɕ��匾���l�M�����Ȃ�❗
����Ȃ��ƌ��������玩���ō������ƁA
��6�̖l�͂������B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���Ώ̂Ȑ}�`�ɂ��ā^19.04.30�n
���ɂ����Ώ̂͂���܂���ˁB
�Ȃ̂ő��̐��Ώ̂��A�o�����������͂����Ǝv���܂��B
�K���������̈Ă��̗p���ĉ�����Ȃ��Ă������ł���B
�����m��ҁn�F�A�����肪�Ƃ��D����̈Ӗ����͂����肳����Ɓu���Ώ̂̎�ނ����ɂ�����v�Ƃ������Ƃł�����C����Ȃ��Ƃ͂���܂���D���ɂ���̂́C��]�Ώ̂�ʑΏ̂Ȃǂł��D�u�ȊO�ɑΏ̂̎�������v�Ƃ����Ӗ��ł�����C����͂���܂���D
�@�]�v�Șb�ł����C���w�Z�̋��ȏ��ɂ͐��Ώ̂Ƃ����p��͂���܂��C���Z�ł͕��C�Ŏg���܂��D���Z�ɓ������Ƃ���ɁC���܂ł̘b�͊ԈႢ�ł����ƌ���ꂽ�獢��̂ŁC���߂��獂�Z�̗p��ɂ��낦�Ă��܂��D
���m�ʂ̕ł���̎���ɑ���n[�����̕ό`�i�������j�ɂ��ā^19.04.22�n
������悤�ɂȂ�܂����B
���肪�Ƃ��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�P�����Ƒ������ɂ��ā^19.04.21�n
�l�I�ɂ�������Ă������悩�����Ǝv�����B
���p�����lj�����̂͂ǂ��ł��傤�B
���̉��@�͂��Ȃ�D���ł�!
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����i�S����,����,�����j�ɂ��ā^19.04.21�n
�Ӗ���������Ȃ��@�Ȃɂ��ǂ����Ă��̍l���ɂȂ�̂��H�@��������������₷�����Ă���邱�Ƃ����肢���܂���
�����m��ҁn�F�A�����肪�Ƃ��D�S����,����,�����Ȃǂ́C���Ȃ̂ŗ��R����������܂���…�������߂����炻���Ȃ��Ă���̂ł��D
1+1�́C�Ȃ�2�ɂȂ�̂��ƕ����Ă����ʂł��D�������߂����炻���Ȃ����̂ł��D
���m�ʂ̕ł���̎���ɑ���n[���̐��E���̐� �P���ɂ��ā^19.04.20�n
���w��N�ɂȂ�������ł������ǁA�ƂĂ��ȒP�ł����B
�@�@�@�C��t���āA������x�A���g�݂܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���̉��@�E���@�ɂ��ā^19.04.19�n
���K��������̂ɂ͂ƂĂ����x�ǂ������ł�!!
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�P�����Ƒ������ɂ��ā^19.04.19�n
2(3a+b)�͓W�J���Ȃ��Ă��A�������ɂȂ�̂ł���?
�����m��ҁn�F�A�����肪�Ƃ��D�u�������ɂȂ�v�Ƃ������t�́C���Ȃ�d�����t�Łu�������ł���v�Ƃ����Ăق������ł��D���Ȃ킿�C���w�ł́C�u�^���͐����ł���v�Ƃ�������͂Ƃ�܂���D�Ⴆ�C����咣���^�ł��邩�ۂ��́C�q�ϓI�ɔ��f�������̂ł����āC�吺��100���ΐ^���ɂȂ�ƌ����悤�ȗ���ɗ����܂���D
�@���鎮���������ł��邩�ۂ��́C���̕\���ɂ���Ăł͂Ȃ��C���̎��̐��藧���ɂ���Č��܂�C�W�J�����Ƃ��ɁCn�����̘a�ɂȂ鎮�́C���ׂđ������ł��D
���m�ʂ̕ł���̎���ɑ���n[�����̕ό`�ɂ��ā^19.04.18�n
����(�P)�ɂ���
����ł�x���E�ӂɈڍ������-y=-x+3�Ƃ���܂���
�ʉ��Ƃ���-y=-(3-x)�ł͂����Ȃ��̂ł���?
�����m��ҁn�F�A�����肪�Ƃ��D����̓_���ł��D
�@�܂��C�r���o�߂͎��R�Ƃ��āC�����������������ǂ����������ׂ�ƁC-(3-x)��-3+x�Ȃ̂ŁC-x+3�Ƃ͕������t�ł��D
�@���ɁC�ό`�̓r���o�߂����������ǂ����ׂ�ƁCx-y=3��-y=-(3-x)�̕ό`�́Cx���ڍ����Ă��炳��ɉE�ӂ̕��������ς��Ă���C���̂悤�ȕό`�͂���܂���D
�@���w���̒i�K�ŁC�Ԉ�����ό`���@���g�ɒ����Ă��܂��ƁC�Ȃ��Ȃ�����܂���D�܂�Ȃ���ł����C�U�M�g���̃A�{�J�h�Ƃ����ׂ��Ƃ�����C�U�g�M���̃A�{�K�h�Ɗo���Ă��܂��ƁC���̉��{��������������K���Ȃ��ƁC���ɖ߂�܂���̂ŋC��t���܂��傤�D
���m�ʂ̕ł���̎���ɑ���n[�����i�S����,����,�����j�ɂ��ā^19.04.17�n
�e�X�g�O���ɂ��̃y�[�W���݂ė��K�����疞�_���Ƃꂽ�̂ł����������������ł��B�{���ɂ��肪�Ƃ��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D����͂悩�����C�Ƃ����ׂ��Ȃ̂ł����C���z�R���@�蓖�Ă��̂ŁC��������@�蓖�Ă���Ƃ͍l���Ȃ������悢��������܂���D���ǂ́C���Ȃ��̓w�͂łł����̂��C�ƍl���������X�v���X�ɂȂ�Ǝv��
���m�ʂ̕ł���̎���ɑ���n[�������ɒ������K�ɂ��ā^19.04.15�n
�����˂��̂���
�����m��ҁn�F�A�����肪�Ƃ��D�������t���g������C�����݂��������肷��ƁC�l�������邾���łȂ��C�ł���Ȏ������g�������܂��D����͒������Ɛ����Ă���ƁC�ς���ς����Ēi�X�ƕ������Ă��邱�Ƃł��D
�@���āC���ʼn��Ǝv���I�������N���b�N����ƁC�̓_���ʂƉ�����o�܂��D���̋��ނł͉���y�[�W������P�P�̃y�[�W�ɁC���̂悤�ɂ͏����Ă��܂��C�S���̃y�[�W�ł��������\���ɂȂ��Ă��܂��D���߂̕��̃y�[�W�ŁC�e�X�g���ƉƂ���������̎��f�[�^�̂������Ƃ����v�����݂̂���ꍇ�����蓾�܂��̂ŁC���̃y�[�W�ɂ́C�̎d�����ꌾ��������ł����܂��D
���m�ʂ̕ł���̎���ɑ���n[�l���v�Z�̗D�揇���ɂ��ā^19.04.14�n
�Ȃ��O���珇�Ɍv�Z���Ȃ��Ɛ����ł��Ȃ��̂�
�����m��ҁn�F�A�����肪�Ƃ��D����̈Ӗ���������Ȃ��̂ŁC�ꍇ�������ē����܂��D
�A�j ���̃y�[�W�̋��ނɂ��āC�u�O���珇�Ɍv�Z���Ȃ��Ɛ����ł��Ȃ��̂��v�Ɛq�˂Ă���̂ł���C��납�珇�ɉ��Ă��̓_�ł��邩��C���₪�Ԉ���Ă���D
�C�j �����Z��|���Z�̂悤�ɓ����ʂ̌v�Z������Ƃ��C�u�O���珇�Ɍv�Z���Ȃ��Ɛ����ł��Ȃ��̂��v�Ɛq�˂Ă���̂ł���C��납�珇�Ɍv�Z���Ă����������ɂȂ邩��C���₪�Ԉ���Ă���D
(x+y)+z=x+(y+z)�����藧����C�O�������Ă���납�����Ă������ɂȂ�D������Cx+y+z�Ə������Ƃ��ł���D���̏ꍇ�́C�ւ��Ȃ���`���Ƃ��Č�납����Ȃ��Ă��C�O����������悢�D
3+(4+5)=3+9=12 ←→ (3+4)+5=7+5=12
(xy)z=x(yz)�����藧����C�O�������Ă���납�����Ă������ɂȂ�D������Cxyz�Ə������Ƃ��ł���D���̏ꍇ�́C�ւ��Ȃ���`���Ƃ��Č�납����Ȃ��Ă��C�O����������悢�D
�E�j �a���ƐϏ����������Ă���Ƃ��́C���̕łɏ����Ă���悤�ɁC�D�揇�ʂ̍����Ϗ����ɍs���D������C�u�O���珇�Ɍv�Z���Ȃ��Ɛ����ł��Ȃ��̂��v�Ɛq�˂Ă���̂ł���C���₪�Ԉ���Ă���D
�RX�{�R���̂QX�|�P
�����m��ҁn�F�A�����肪�Ƃ��D���̃y�[�W�́C���w�Z1�N�������́u���̒l�v�̃y�[�W�ł��D�������̏��������̂��C����ɂ��Ȃ��Ă��Ȃ����ƂɋC�t���Ă����Ȃ��ƁE�E�E�����������₪�Ԉ���Ă��邱�Ƃ�������܂����H
���m�ʂ̕ł���̎���ɑ���n[�~�ɓ��ڂ���l�p�`�ɂ��ā^19.04.11�n
�킩��Ȃ������̂ł��肪�����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�P���������̉������ɂ��ā^19.04.11�n
������l�ł����A���������Ăǂ������������ƌ������Ă��̃y�[�W�ɂ��ǂ蒅���܂����B�ƂĂ�������₷���ėǂ������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���������ɂ��ā^19.04.10�n
���̉��т����肵�������ȁH����������ƃL���C�ɕ��ׂ��肵���������������B�@
���̎��͂����I���ɂ����Ă��₷���I�����I�Ȗ��Ŏ��ƂŖ𗧂I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�_�Ώ̂Ȑ}�`�ɂ��ā^19.04.08�n
�Ӗ���������܂���
�����m��ҁn�F�A�����肪�Ƃ��D���ꂾ���ʼn�b�����藧�͖̂����ł��傤�D���Ȃ��͉��N���H���܂ʼn����w��ł����̂��H�����ǂ�������Ȃ��̂��H
�@���ނ����P���悤�Ƃ����l���̐l�́C���̂悤�Ȕ����͂��܂���D
���m�ʂ̕ł���̎���ɑ���n[�����̉��p�ɂ��ā^19.04.08�n
�Ӗ����킩��Ȃ�
�����m��ҁn�F�A�����肪�Ƃ��D���p���ł��̂ŁC�����Ȑl������܂��D
���m�ʂ̕ł���̎���ɑ���n[���E�����i�܂Ƃ߁j�ɂ��ā^19.04.06�n
������������₷�������ł��B���肪�Ƃ��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�P���������̉������ɂ��ā^19.04.03�n
������Â炢�c�c�Ǝv���܂�😔😔���w1�N
�����m��ҁn�F�A�����肪�Ƃ��D���������܂��K���Ă��Ȃ��V�������X���X�������̂́C���Ƃ��Ɩ����ł��傤
���m�ʂ̕ł���̎���ɑ���n[�P�����̕��͑��ɂ��ā^19.04.03�n
�����b�ɂȂ�܂��AG�Ɛ\���܂��B
��L�A5/6�̌g�т̓d�b�����̖��Ōv�Z���55.55�E�E���A�l�̌ܓ��ł�56���ł����A������56���ɂ����5016�~�A55���Ƃ����4980�~�A�E�E
5000�~�ȉ��ɂ���ɂ�55���ł͂Ȃ����Ǝv���Ă��܂��܂��B
�ǂ��l����悢�̂ł��傤���E�E
�ƂĂ��������ɖ��������b�ŁA���l���Ƃ͎v���܂���B
��낵�����肢�������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D���������Ă����Ȃ��ƁC�����ɂ����ł��D�����ɂ���������肪�����Ă���̂ł͂Ȃ��C�����������v���O�����łł��Ă��܂��̂ŁC100�Ă��������Ă��������͏o�Ă��܂��C��҂��ǎ҂����Ă�����Ɠ����������邱�Ƃ��ł��܂���D�����C���ɏ����Ă���܂��悤�Ɂi�����ɂȂ�Ƃ��͎l�̌ܓ����ē�����D�j�Ƃ����Ȃ̂ŁC�l�̌ܓ����ē�����悤�Ƀv���O��������Ă��邾���ł��D
�@�������x50km/h�̓��H�ŁC59km/h�Ŕ����ؕ����ꂽ���Ƃ͂Ȃ��D���̏ꍇ�́C1���͐�̂ĂƂ����ʼn^�c����Ă���݂����ł��D
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝�ɂ��ā^19.04.03�n
������₷���ł�������������������f�ڂ��Ă����Ɠ����̑�ȂǕ��L���g�����Ƃ��ł���Ǝv���܂��B�ł���Ήߋ��̓������ŏo�����������y�[�W���ɓ���Ă����Ăق����ł�
�����m��ҁn�F�A�����肪�Ƃ��D�������Ɗ�{�����y�[�W�ɏ����͖̂����ł��D�T�u���j���[�œ������̃y�[�W�����Ă��������D
���m�ʂ̕ł���̎���ɑ���n[�A���������i���Z�������j�ɂ��ā^19.04.01�n
A�FB���Q�F7
4A�{B���|15
�݂����Ȃ̂͂ǂ�����Ă��܂����H
�����m��ҁn�F�A�����肪�Ƃ��D���w�Z�Z���̔�Ꭾ�ŏK���u�����̐ςƊO���̐ς��������v�Ƃ����̂��g���āC���ʂ̕������ɒ����Ƃ��ł��傤�D
A:B=2:7 → 7A=2B …(1)
4A+B=−15 …(2)
(2)��(1)�ɑ�������
7A=2(−4A−15)
15A=−30
A=−2, B=−7
���m�ʂ̕ł���̎���ɑ���n[�Q���������̉������ɂ��ā^19.03.31�n
������Ɠ���ł����A������]����������Ɂu���[�Ȃ�قǁv�Ɣ[���ł�����e�Ȃ̂łƂĂ����̃T�C�g�ɂ͏������Ă��܂�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�W�J�����@(x+a)(x+b)�ɂ��ā^19.03.25�n
���ۂɉ����Ă݂č̓_���ł���̂ŏ�����܂����I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�l���v�Z�̗D�揇���ɂ��ā^19.03.24�n
���ʂɕt���������̌v�Z�ɂ��Ă�������Ă���������ƍK���ł��B
-(-1)^2�̌v�Z������
-(-1)���D��ł��傤���A���邢��(-1)^2���D��ł��傤���B
�O�҂ł���A1^2=1�A��҂ł����-(1^2)=-1�ƂȂ�܂��B
�i�\�v�Z�\�t�g�ł͑O�҂ƂȂ�܂��j
�����m��ҁn�F�A�����肪�Ƃ��D���ʂ́C���̃y�[�W�̐擪�ɏ����Ă��܂��悤�ɍŗD��ł��D
�@���w�ł́C-(-1)^2=-1^2=-1�ł��DExcel�ł� =-1^2��1�ł��D�����Excel�̕Ȃ��ƍl����悢�ł��傤�Da1��-1�Ə����Ă����āCb1��=a1^2�Ə����C1�ɂȂ�܂��D
�R���s���[�^�����錋�ʂ́C�u�����n���Ƃ̖��v�ƍl����̂��悭�C�ǂꂪ�������Ăǂꂪ�Ԉ���Ă��邩�ƍl���Ă����ɗ����܂���D�����Ƃ����|�p�́��������������āC���������Ԉ���Ă���Ƃ͍l���Ȃ�����Ƃ悭���Ă��܂��D
Excel, Javascript, Python�ł̉��Z�q�̗D�揇�ʂ������r�������̂́C
���̃y�[�W�̉��[�ɂ���܂��D
65�̎�K���ŁA�]�g���Ŏn�߂Ă��܂��B��낵�����肢���܂��B
���āA�ԈႢ�̎w�E�ł����܂���ł��B���w���w2�N���̈ꎟ���A�ω��̊����Q�i�ω��̊����i�����j�j�A�ω��̊����̗�P�̏�ɂ���g�̐������u�i x �̑����ʁj���i y �̑����ʁj�Ƃ�������Z�ɂȂ�̂Œ��ӂ��邱�ƁD�v�͊ԈႢ�ł͂Ȃ��ł��傤���B�ύX�����҂��m�[�g�ɏ����ʂ��ĕ����āA�n�e�H�Ⴄ�ȂƎv���܂����B�i �� �̑����ʁj���i �� �̑����ʁj�������̂ł͂Ȃ����Ǝv���܂��B
���̊��Ⴂ�łŕ����Ă���\�������܂���B
�����m��ҁn�F�A�����肪�Ƃ��D���̓~�X�ł��̂Œ������܂����D
��ʌ��m�}�c�W�W����^19.03.21�n
65�̎�K���Ŕ]�g���̂��߁A������萔�w���ȑO��苻��������A���p�����Ă��������Ă���܂��B���Z�҂܂ōs�����������Ǝv���܂��B��낵�����肢���܂�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�O�p�ɂ��ā^19.03.20�n
�ƂĂ��A������₷�������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���������ɂ��ā^19.03.19�n
Good game.
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����̐����ɂ��ā^19.03.19�n
�ƂĂ������I�킩��₷���I�ō��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�P���������̉������ɂ��ā^19.03.17�n
�ƂĂ��킩��₷����
��
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������̕��͑��ɂ��ā^19.03.11�n
��肪�ǂ݂ɂ�������
�����m��ҁn�F�A�����肪�Ƃ��DPC�p�̃y�[�W���X�}�z�œǂ�ł����܂����C�y�[�W�̐擪�ɏ����Ă���܂��悤�ɁC�X�}�z�p�̃y�[�W�͕ʂɂ���܂�
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝�ɂ��ā^19.03.11�n
�u�ʁv���Ǝv���Ă��̂ł����u�ǁv�Ȃ̂ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D�����ϊ��~�X�ł��̂Œ������܂����D�i�S���ǂ̓ǂ݉߂������j
���m�ʂ̕ł���̎���ɑ���n[�u���������v�̂͂������ɂ��ā^19.03.10�n
����͂ƂĂ������I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���̂̕\�ʐ��ɂ��ā^19.03.09�n
���9�̃q���g�̒��ɂ���(�Q)��(�P)�͂ǂ����������R�Ŋ���̂ł��傤��
�����m��ҁn�F�A�����肪�Ƃ��D�����Ă݂��番����܂��F


�����܂�����C����

�����܂�D
���m�����������iH31�j�̐��w
���R�́i1�j�`�i3�j��������肢�ł��܂��ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��D
���_���猾���Ζ����ł��DH31�N��H31�N�x����1�N�Y���܂����C��������e�X�̊w�K�m�����F�̃Z�b�g�����J���Ă��܂����C���̂ǂ������ӏ����s���Ȃ̂��C�����ɑ���Ȃ��v�����q�ׂĂ��������Ȃ��ƁC�������ĂɂȂ�̂ł͂Ȃ��ł��傤��
���m�ʂ̕ł���̎���ɑ���n[�������ɒ������K�ɂ��ā^19.03.07�n
11.1�͂ǂ����܂����H
�����m��ҁn�F�A�����肪�Ƃ��D
�ǂ����܂����ł͎���ɂȂ��Ă��܂��C�����ɂ�����ǂ��Ȃ�̂�������Ȃ��Ƃ������₾�Ƃ��܂��傤�D��肪���������Ă���̂ɁC�����ǂ�ł��C�{���ɕ�����Ȃ��̂ł����H

�o��(��+��)(��+��)�p�̌v�Z�͂ǂ̂悤�ɂ����炢���̂ł��傤��
�����m��ҁn�F�A�����肪�Ƃ��D
(1) �u���������v�̂͂������Ƃ����y�[�W�ł����C������̖��ł͒��������͉������ɗ����Ă��܂���D�܂�v��܂���D
(2) ���ɁC�Z���������̂��Ȃǂł���ꍇ�C3(x+2)(x+4)�̂悤�Ȗ��́C���w2�N�ł͈����܂���D���w3�N���̓W�J�����̃y�[�W�����Ă��������D
(3) �Z�����̏ꍇ�F3(2+3)(4+5)�̂悤�ȏꍇ�C�{���͊ԂɊ|���Z�̋L�����K�v�ł����C�|���Z���ȗ�����Ă���ꍇ�ɂ́C3�~5�~9�̂悤�Ɍv�Z����Ώ\���ł��D
���m�ʂ̕ł���̎���ɑ���n[���̂̕\�ʐ��ɂ��ā^19.03.01�n
������ł�
�����m��ҁn�F�A�����肪�Ƃ��D�u�v���u�v
�Ǘ��l�ɂ́C���ނ����P����ӎu�͂���܂����C���̊��z�ł͂ǂ��ɂ��Ȃ�܂���D
• �N�ɂƂ���…��1�Ő��w���s���ӂ����������͓̂��R�ł��傤
• �ǂ̖�肪…���ꂪ�����ĂȂ���C�����ǂ������̂��������t���Ȃ�
• �ǂ�����̂�…�����̂��Ƃŏ������݂ɂ����Ƃ������Ƃ��q�ׂĂ���̂��C�����������w�̓��e��������Ȃ��Əq�ׂĂ���̂��������ĂȂ�
�ȏ�̂悤�Ȗ�ŁC�����������z�𑗂��Ă��炢�܂������C���ނ̉��P�Ƃ������Ƃɂ��āC�u���_����̓I�ɒ�N���āC��̓I�ɉ�������v�Ƃ����ϓ_����͎Q�l�ɂȂ�܂���ł����D�i���܂������Ă��炤�K�v�͂���܂��C�����̒u����Ă���ɂ��ĉ����L�q���Ȃ��āC�����u����v�����ł͂ǂ��ɂ��Ȃ�܂���j
?�m�Ђ܂�肳��^19.02.23�n
�F�X�ƎQ�l�ɂȂ�܂�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝�ɂ��ā^19.02.24�n
������Ƃ����������������炩�����ł��B
���ǁA���������Ċy���������ł��I
���肪�Ƃ��������܂�😊
�����m��ҁn�F�A�����肪�Ƃ��D
?�m�Ђ܂�肳��^19.02.23�n
�F�X�ƎQ�l�ɂȂ�܂�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���̂̕\�ʐ��ɂ��ā^19.02.23�n
���ɗ����܂����_(^o^)�^
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����͉����H �ɂ��ā^19.02.23�n
�ǂ���😆
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[��i�@�ŕ\�킳�ꂽ���̘a�ɂ��ā^19.02.23�n
�o���o���̕��n�Ő�A��15�_���Ƃ������Ƃ̂���o�J�ł��킩��₷�������ł��I���ꂩ������p���čs�������Ǝv���܂�👍
�����m��ҁn�F�A�����肪�Ƃ��D�Ǘ��l�����C���o�Ă����D
���m�ʂ̕ł���̎���ɑ���n[�ő���ƍŏ����{���ɂ��ā^19.02.22�n
�킩��ɂ���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�O�����̒藝�̉��p�ɂ��ā^19.02.22�n
������킩��Â炢
�����m��ҁn�F�A�����肪�Ƃ��D���̃y�[�W�͉��p���Ȃ̂ŁC��{�̃y�[�W�ł����������K���Ă���łȂ��ƁC����ł��D
���m�ʂ̕ł���̎���ɑ���n[�A���������i����@�̂₳�������j�ɂ��ā^19.02.22�n
���P�́i�R�j�́A����-1/7�ł͂Ȃ��ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D�������܂����D
���m�ʂ̕ł���̎���ɑ���n[�O���t�������̎��ɂ��ā^19.02.21�n
���������Z�����ł�(^^;;
�����̕����S�R�킩���ĂȂ������̂ł����A������������₷�������ƁA���₷���z�F�łƂĂ����ɂȂ�܂����I�L��������܂����I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�H�����̔Z�x�ɂ��ā^19.02.13�n
���K��肪�����ē��e��[���������邱�Ƃ��ł��܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�H�����̔Z�x�ɂ��ā^19.02.13�n
�H�����̎���������Ă����������҂ł�
�����Ɠǂ߂킩�鎖�Ȃ̂ɓlj�͂��Ȃ����܂�ڒ����Ȏ�������Ă��܂����݂܂���B
�ɂ�������炸���J�ɑΉ����Ă������芴�ӊ����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�H�����̔Z�x�ɂ��ā^19.02.11�n
�ǂ����Ă������ɓ�q���Ă��邽�ߎ��₳���Ă��������܂��B
���Z�����Ƃ��낷�݂܂���B
������̃y�[�W�ł�����
�H���̏d���̍��v�� 200�~0.12 + 300�~0.07=45(g)�C
�H�����i=�H��+���j�̏d���̍��v�� 200+300=500(g)�C
�H�����̔Z�x�� 45��500�~100=9(%)
�Ƃ���܂����A����܂ł̉���ɂ��ƁA
���̏ꍇ�H�����̏d���́A���Ɛ��𑫂���545g�Ōv�Z����̂���
�l���Ă����̂ł����A����ȍ~�S�ė��̌v�Z���ɂ�
�H�����̏d���ɉ��̏d���������ꂸ�Ɍv�Z����Ă���̂������o�����c
�l�������ǂ����Ԉ���Ă��܂��ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D�H�����i=�H��+���j�̏d���ɂ́C���łɐH���̏d���������Ă��܂��D
���m�ʂ̕ł���̎���ɑ���n[�H�����̔Z�x�ɂ��ā^19.02.07�n
質問です…、E2%の食塩水500gに4%の食塩水を??g混ぜると9%の食塩水になる」??に入る数孁E
⤴のような問題�Eどのようにとけ�EよろしいでしょぁE��。。、E
�����m��ҁn�F�A�����肪�Ƃ��D�Q���U�������Ƀv���o�C�_�[�l�ɂ����ăT�[�o�����e��Ƃ�����C���̌��ʁCSend-mail CGI�̊����ϊ��ɃG���[�������Ă���悤�ł��D���̋��ނ̊Ǘ��l�́C���[�U�Ƃ��ăf�[�^�t�@�C�������������Ă��܂��C�v���o�C�_�l�ɑΉ����˗����邵���Ȃ��ł��D
�����M���ꂽ�����̊����R�[�h���CUnicode,UTF-8,Shift-JIS,jis,EUC,������C�؍���C��p��Ȃǂǂ�ɕϊ����Ă��ǂ߂܂���ł����̂ŁC�v���o�C�_�l�̑Ή��҂��Ƃ������ƂŁC���炭���҂����������D����܂ł͓ǂ߂܂���̂ʼnł��܂���D
���G���[�̌X���Ƃ��āCShift-JIS�̃R�[�h��UTF-8�ɕϊ�����Ă���悤�ł����C�t�ϊ����|���Ă��ꕔ�����ǂ߂܂���D
��2019.2.6�ȍ~�Ɏ�M�������z���͂��ׂĂ���ɊY�����܂��D���炭�����f�����������܂���
�� ?�m #�K���p�ԉ���������^19.02.05�n
�����������╶���ɐF��������Ȃǂ��킢���Ă������Ǝv���܂�(�B-_-�B)
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�P�����Ƒ������ɂ��ā^19.02.05�n
�܂�A
��j8x��������1
����Ȃ��ł����H
���Ⴀ���̎���1�������Ă��Ƃł����H
�����m��ҁn�F�A�����肪�Ƃ��D 8x�͂P�����ł��D
���m�ʂ̕ł���̎���ɑ���n[�ꎟ�������i�������ƌ��Z�̎d���j�ɂ��ā^19.02.01�n
���������āA������Â炢�������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D 320�~568��iPhone��PC�p���ނ�ǂ�ł�����悤�ł����C
�g�їp������܂��̂ł������ǂ�ł��������D
������������₷�������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D����ł��ӌ��ł��Ȃ��C���z���ꌾ�̏ꍇ�́C�Ǘ��l���@�B�I�ȉ������Ă���悤�Ɍ����܂����C�ǂ̂悤�ȃy�[�W���u�����ˁI�v�Ȃ̂����������Ă��܂��D�Ǘ��l����J���č���āC�悭�ł����ƍl����y�[�W�ƁC�ǎ҂��u�����ˁI�v�Ƃ����y�[�W�Ƃ́C�K��������v���܂��C���̂[���͈�v�����悤�ł��D
���m�ʂ̕ł���̎���ɑ���n[�������ɒ������K�ɂ��ā^19.01.29�n
���̖��̗�A�ƂĂ�������₷�������ł��I
������Ȃ���肪�������̂ŁA�Q�l�ɂȂ�܂���👍
���肪�Ƃ��������܂���😊
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝(�������)�ɂ��ā^19.01.24�n
�ƂĂ��Q�l�ɂȂ�܂����B�w�Z�̖��ł́@�����܂ōl���邱�ƂȂ������ł�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝�ɂ��ā^19.01.24�n
�����Ƃ�肽���Ȃ��� ���肪�Ƃ�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������̉��̌����ɂ��ā^19.01.19�n
��ς킩��₷����������Ă���A���肪�Ƃ��������܂��B
�Ƃ���ŁA2���������̉��̌����̏ؖ��ŁA�E��̂ɍs�����Ƃ����2�s�ڂ�3�s�ڂ�����Ă��܂��B
3�s�ڂ�-(b^2/4a^2)+(c/a)�����ӂɈړ������悤�Ƃ��Ă����̂ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D�������܂����D
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝�ɂ��ā^19.01.18�n
���������ɂȂ����I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���̕ψ��ɂ��ā^19.01.17�n
������������₷�������I�I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝(�������)�ɂ��ā^19.01.16�n
�e�X�g�O���Ȃ̂łƂĂ����ɗ����܂����I���肪�Ƃ��������܂�
������ƂĂ��킩��₷�������ł�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���̂̕\�ʐ��ɂ��ā^19.01.16�n
���9���s���S�ł�
�����m��ҁn�F�A�����肪�Ƃ��D�����ƁC�O�̖�肩��`���R�s�[���Ă���C���g���������������Ƃ�Y��Ă����悤�ł��D�������܂����D
���m�ʂ̕ł���̎���ɑ���n[�����}�`�ƕӂ̔��ɂ��ā^19.01.14�n
���߂Ďg���܂����B�{���ɂ��肪�Ƃ��������܂��B
��肪���荂�Z�����̕s���v�f��1�����Ȃ�܂����I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝(�������)�ɂ��ā^19.01.13�n
�ƂĂ��ǂ����ł����B
�Q�l�ɂ����Ă��������܂��B
�s���{���ʂ�1������Ɨǂ��Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�����̌����C�ɂȂ�Ƃ������z�͕�����܂����C47��������Ƒ��߂��܂��D���̃y�[�W�ł́C�����ڂ̃e�[�}���ɐ������Ď��Ă��܂��D
���m�ʂ̕ł���̎���ɑ���n[�O�p,���p�`�ɂ��ā^19.01.13�n
�厖�ȏ��͐ŋ������Ă����ĂƂĂ��킩��₷���ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~�ɓ��ڂ���l�p�`�ɂ��ā^19.01.12�n
���ɏ�����܂���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝�ɂ��ā^19.01.08�n
�i���w�Z�̐搶�̕��̂悤�ł����C�U���I�ȕ��͂ɂȂ��Ă��܂��̂ŁC�̂f�ڂ��܂��j
�����m��ҁn�F���w�Z�̋��ȏ��ł́C�قƂ�ǂ̏ꍇ
��x�̂悤�ɏ�����܂����C���Z�i�w��95%�Ƃ�������ŁC���Z�ł͂قƂ�ǂ̏ꍇ

�ȂǂƏ����܂��D�܂�C���w�Z�ł��̕������撣���Ă��C1�N�o�ĂΕ��ʂ͂��������Ȃ��Ƌ����Ȃ���Ȃ�Ȃ��̂ŁC�����������Ă���������k�ɂƂ��Ă͍��������Ȃ��ƍl�����܂��D
�@���ɂ��C�悭���鋳�����Ƃ��āC�����Ɋ|���Ă���萔���W���Ƃ������Ƃ���C

��

�͌W���ł͂Ȃ��Ɗ撣���ċ�����搶��������悤�ł��D�������C���Z�ł�

�̂Q�̉���

�Ƃ���Ƃ��C

�ƂȂ邱�Ƃ����ƌW���̊W�Ȃǂƌ����܂�.���̗�ł́C

�͌W���ł͂Ȃ��Ɗ撣���Ă��炤���́C

���W���Ƃ��Ă��炤���������������܂��D
���7�̖�蕶�ƑI�����������Ă��Ȃ��悤�ł�
�����m��ҁn�F�A�����肪�Ƃ��D���̃R�s�y�ɂȂ��Ă��܂����̂ŁC�������܂����D
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝�ɂ��ā^19.01.08�n
��قǃA���P�[�g�𑗐M�������̂ł��B��قǂ̕��ɕ⑫���܂��B�C���̕ӂ�v�Ƃ����̂́A��3���獂1���x���̐��w�Ƃ����Ӗ��ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝�ɂ��ā^19.01.08�n
�͂��߂̌�.���Ƃ� �̂Ƃ���ŁA�I�ՂɁA�C��AB�Ƃ��������Ƃ��v�Ƃ���̂ŁA�����肢�܂��B���ƁA���z�Ƃ��ẮA�ȒP�Ȗ�肩�班��������܂ł���A�m�����蒅���Ă����̂�������܂����I�����͒�2�Ȃ�ł����ǁA�咆�w���A���悤�Ǝv���Ă��܂��B���̂������炱�̕ӂ�̕��͂��Ă����������ǂ��ł���ˁB���肢���܂��B�������炵�܂����B
�����m��ҁn�F�A�����肪�Ƃ��D�A�C��AB�Ƃ��������Ƃ��v���A�C��AB�Ƃ����Ƃ��v�C�������܂����D���Q�����w������Ƃ́C�ғ��w�������ȁH
���m�ʂ̕ł���̎���ɑ���n[���P.�������̉���Ɨ��K�ɂ��ā^19.01.08�n
���4��(1)�Ő�����I�Ԃƃo�c���o�܂�
�����m��ҁn�F�A�����肪�Ƃ��D�������܂����D�i���퐶���łP�Ԃ��v���O�������0�C�Q�Ԃ��vۃO�������1�Ƃ���Ƃ�����C���퐶���̕��̔ԍ������Ă��܂����̂ŁC����Ȃ��Ȃ��Ă��܂����j
���m�ʂ̕ł���̎���ɑ���n[�Β��p,���ʊp,���p�ɂ��ā^19.01.07�n
�e�X�g�O�������̂ł���Ă݂܂����I
��������Ă���̂ł킩��₷���A�ƂĂ��Q�l�ɂȂ�܂����B
�ł����A���ȏ��̖�肪�����Ƃ�������肻�����s�ւł����c�c(�ؖ��̖��)
�X�}�z�Ŗ�肪������Ȃ�Ă������y�����ł������A���ɂ��Ȃ�܂����B
���ꂩ������X��������҂��Ă���܂��B
���肪�Ƃ��������܂��I
�����m��ҁn�F�A�����肪�Ƃ��D�O�p�`�̓��p�̘a�Ȃǂ̏ؖ����Ȃǂ́C�T�u���j���[�����ǂ�Ƃ��̌�̍��ڂɂ���܂��D
���m�ʂ̕ł���̎���ɑ���n[�������̕\�����ɂ��ā^19.01.07�n
���4��(2)�ɂ͐�����2����̂ł�
�����m��ҁn�F�A�����肪�Ƃ��D�����ƁC���̗�����낤�Ƃ��āC�M�҂�㩂�...�������܂����D
���m�ʂ̕ł���̎���ɑ���n[�P���������̕��͑��ɂ��ā^19.01.06�n
���̎�ނƂ��Ď��Ԃ̖�肪���Ȃ̂ł����A��ނ̒��ɂȂ������̂ŏ����c�O�ł����B����ȊO�͂ƂĂ��g���₷��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D�P�O��
���Ԃ⑬���������Ă���y�[�W������܂��̂ŁC����������Ă��������D
�����̈��������̌v�Z�̎d����������Ȃ��̂ŋ����Ă��ꂽ�炤�ꂵ���ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�����̈��������Ƃ͉��̂��ƂȂ̂��C���������Ƃ��Ȃ��ł��D���t�ʂ�ɂƂ炦��C����ƕ��q�����ꂼ��i�f�j����������������̂ł͂Ȃ����D
�@�Ƃ������C���̃y�[�W��2���������̉������̃y�[�W�Ȃ̂ŁC�u�����W���̂Q���������v���������߂ɁC������������v�Z�̎d����������Ȃ��ƌ����Ă�����̂Ȃ�C����͍l���Ȃ��Ă��悢 - - �܂�C������Đ����W���̕������ɒ����ĉ����悢����D
�m��n

�����������Ƃ��C���Z���Ȃ玟�̂悤�ɉ����ꍇ�����邪�C���w���ɂ͂����߂ł͂Ȃ�
(x-\frac{1}{3})=0\rightarrow x=\frac{1}{2},\hspace{3}\frac{1}{3}&chf=bg,s,fff9f9&chco=ff0000)
���̂悤�ɁC������̂��ԈႢ�̏��Ȃ����U�@�ł��D�i���ӂ�6���|����j

���̌������g��



�ƂĂ������ł�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝�ɂ��ā^19.01.05�n
�����Ɖ�����A����Ȃǂ�����̂ŕ�����₷���ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Q���������̉������i�܂Ƃ߁j�ɂ��ā^19.01.05�n
ax2+bx+c=d(d��0)
���̏ꍇ���Ăǂ�����ĉ����̂ł����H������Â炭�Ă��݂܂���B"��"�̍���(���w�Z�̎Z���ł��������̕���)��0����Ȃ��ꍇ�ł��B
�����m��ҁn�F�A�����肪�Ƃ��D����ɂ͍��Ə�����Ă��܂����C�E�Ɖ��߂��ē����܂��D
���̌����ɂ��
&chf=bg,s,fff9f9)
�̉���

�ł��D������
=0\hspace{5}(a\ne 0)&chf=bg,s,fff9f9)
�̉���
}}{2a}&chf=bg,s,fff9f9)
�ł��D�i

���ڍ����邾���ł��j
�ǂ���ƂĂ��킩��₷���ėǂ������ł��B
���͎��ł��B�����Ŏ���Ȃ̂ł����A�����n�̕��͂ǂ̂悤�ɂ��Ηǂ��ł����H
�Ȃ�ׂ��ԐM���Ăق����ł��B2���ȓ��ɂ́B�ǂ������肢���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D����̈Ӗ����m���߂܂����C���Ȃ��͒��w3�N���ł����D�����n�Ƃ����̂́C�w�Z�������n�Ƃ������ƂȂ̂��C���Ȃ␔�w�̊w�K�Ƃ������ƂȂ̂��H���܂łǂ�ȕ������Ă����̂ł���- - ����ɂ���āC�œK�헪���ς��܂��D
�@���������܂܂łǂ�ȕ������Ă��āC�ǂꂭ�炢�̎��͂ŁC�ǂ�Ȗ�肪�o��w�Z�Ɏ����̂��C�Ȃǎ���҂̃f�[�^���Ȃ���ԂŁu���ꂪ�����������@�ł��v�ȂǂƎ��M���肰�ɏq�ׂ邱�Ƃ͂ł��܂���D���̋��ނ̊Ǘ��l�́C�肢�t�ł͂Ȃ��̂ł��D
�@�w�Z�ɍs���Ă���̂Ȃ�C���Ȃ��̂��Ƃ��悭�������Ă���S�C�̐搶�ɕ����̂��x�X�g�ł����D
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝�ɂ��ā^19.01.3�n
�~���p�ƒ��S�p�̊W�͏��߂Ēm��܂������A���̖��͊ȒP�ł����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�O�p�ɂ��ā^18.12.31�n
�A�j���[�V�������킩��₷�������ł��B�l�N���ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝�ɂ��ā^18.12.30�n
���A�w�Z�ŏK���Ă��Ȃ��Ƃ��낾�����̂ł����A������₷���ď�����܂����I�I
�m�ł����Ă��������ł��I
���肪�Ƃ��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝(�������) �ɂ��ā^18.12.29�n
�Ƃ��Ă������Ƃ������܂��B👍🏻������50�������̂łȂ����Ă�������
�����m��ҁn�F�A�����肪�Ƃ��D�Ȃ�ق�...�S��قǑ����悤�ł����C�u���p�v�Ȃ̂ŁC���̐��l�����ρE�ҏW���邱�Ƃ́C�����쌠�҂̓��ꐫ�ێ����Ƃ̌��ˍ����Ŗ����ł��D�c����@�́C���ނ̏�������ꊷ���āC���������������Ȃ��悤�ɂ�����@�ł����C���ނƂ��Ă͗��Ɏ����������ڂ��Ƃɂ܂Ƃ߂�\�����Ƃ��Ă���̂ŁC����������ɂȂ�܂��D
�@�o�肷�鍂�Z�̑����猩�āC���ꂮ�炢�̊p�x����Ԑ}�����₷���̂�������܂���D���̋��ނƂ��ẮC�u�܂��������������������Ƃ͂Ȃ����낤�v�Ɨ��̗���ǂ�Ŗ����Ă��炦�C�悢�Ƃ������܂��D…�ԍ����̑I����̏ꍇ�ł��C�u�����I�����������͕̂s�K�����v�Əq�ׂ�搶�����܂����C�Z���^�[�����̐��w�ł́u�P�����ƂȂ��肪����=���ʂɗǂ��������C�����l�ł͂P�ɂȂ邱�Ƃ������v�ƌ����Ă��܂��D…�u�����I�����������Ȃ��悤�ɂ���v�ƌ��߂�ƁC�I�����͎����I�ɂP�����Ă��܂��āC�܂Ƃ��ɖ����������́C���ł̉������̃e�N�j�b�N���L���ɂȂ�Ƃ������܂��D
�@����Ȃ킯�ŁC���낢��ƍl����ޗ�������̂ł��D
���m�ʂ̕ł���̎���ɑ���n[�A���������i�����@�j�ɂ��ā^18.12.29�n
�킩��܂�����������ڂ������肢���܂�
�����m��ҁn�F�A�����肪�Ƃ��D���Ȃ��̏ꍇ�́C(1) ����320�h�b�g��iPhone�ło�b�p�̋��ނ�ǂ�ł��܂��D(2) �ǂ̂́C��������5�b�Ԃł��D
(1)
�g�їp�i�X�}�z�p�j�̋�����ǂ�ł��������D(2) �ǂ�ȋ��ނł��C���Ȃ��Ƃ�4���ȏ�͓ǂ܂Ȃ���Ζ����ł��傤�D
�ƂĂ����₷���A������₷������
�����m��ҁn�F�A�����肪�Ƃ��D���₷���Ƃ������Ƃ��d�v�ȗv�f����
���m�ʂ̕ł���̎���ɑ���n[�A���������i����@�j�ɂ��ā^18.12.26�n
Positive points are that it is very easy to understand with several calculators and examples.
Negative points are that it does not contain �s���� version.
Over all, it is fine, but if you may, please add �s���� version.
�����m��ҁn�F�A�����肪�Ƃ��D�p��ŏ����ꂽ���̂�SPAM�������̂ŁC�����Ƃ��ĉ��܂���Dtokyo-ocn�Ȃ獑������ł��傤�D
���Ȃ��̌��Ă���̂́C���w�������̋��ނł��D���{�̒��w�Z�ł́C�A���s�����͈����܂���D
���Z�̋��������Ă��������D
3�Ԃ̍Ō�̖��̓������Ă����Ă܂����H�H
�����m��ҁn�F�A�����肪�Ƃ��D���ɂǂ�ȓ���������̂��C���Ȃ��̍l�������Ă��������D�ʂɒp�ł͂Ȃ��C���k���ԈႢ�₷���X������Ǘ��l���w��ŁC������@�̎Q�l�ɂ��܂��D
���m�ʂ̕ł���̎���ɑ���n[�O�����̒藝�ɂ��ā^18.12.23�n
74�ł��B
�{�P�h�~�ɂƒ��w���w�ɏ����������g��ł���܂��B
���ƁA�l������l��Ȃǂɂ��B
���d�˂�ƂȂɂ��ɂ��č��C�������Ȃ��āA���������̂ł����A�ȒP�Ȗ��ł��A�������Ƃ��ł���Ǝ��Ȗ�������̂��y���݂ł��B
�Ȃ��ł����p�I�Ȃ̂������N���v�Z�B
�����g�����Ƃ��ȒP�ł����A�������킹�p�Ɏg���Ă��܂��B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�̑��Y
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���̒l�ɂ��ā^18.12.17�n
�������m�肽��
�����m��ҁn�F�A�����肪�Ƃ��D���̒l�̖��ŁC������ׂ��l�⎮�������ɂȂ��Ă�����̂́C
���̃y�[�W�ɏ�������܂����C���Ƃ��ƍ��Z�������ł�������ׂ��l�⎮�������ɂȂ��Ă�����̂́C�����Ȃ��悤�ł��D
�ƂĂ��A�Q�l�ɂȂ�܂����B
�L��������܂����I
����������������L��ƁA�����ƕ�����Ղ��Ȃ邵�ǂ��Ǝv���܂��I
�����m��ҁn�F�A�����肪�Ƃ��D����ɃT�u���j���[������܂��̂ŁC�����̃y�[�W������Ă��������D
���m�ʂ̕ł���̎���ɑ���n[���������������ɂ��ā^18.12.09�n
������������n�̗ޑ�P��2�v���X���[�g�R��2��͂Ȃ��P�R�ɂȂ�̂ł���?
�����m��ҁn�F�A�����肪�Ƃ��D�Ȃ�13�ɂȂ�̂ł����Ɛq�˂Ă���̂ŁC�q���g�͌��Ă���悤�ł��D�q���g�ɂ�7+6��13�ɂȂ�Ə����Ă���̂ł����C���w�Z�ȗ�7+6��13�ł��傤�D����ɗ��R������܂����H
���m�ʂ̕ł���̎���ɑ���n[�O�p�ɂ��ā^18.12.09�n
���肪�Ƃ��������܂�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�i���o�[�v���C�X���쐬�ɂ��ā^18.12.09�n
�r���Ŏg���Ȃ��Ȃ�̂ǂ��ɂ����āH
�����m��ҁn�F�A�����肪�Ƃ��D��̓I�Ȏg�p��@��Ȃǂ̗��p�����q�ׂȂ��ƁC�Ή��̂��悤������܂���DAndroid��Chrome�ł͑S�����Ȃ��g���܂��DiPhone��Safari���g���Ă�����悤�ł����C�����s�C��C�u���b�N�ɓ������������Ă���ȂǁC�����̂��������������ł��܂��H
���m�ʂ̕ł���̎���ɑ���n[�P���������ɂ��ā^18.12.04�n
��������10��Ȃ̂ŁA���C���o�܂����I�܂��A�킩��Ǝ��͂ǂ�Ȗ�肩�ȂƊy�����Ȃ�܂����I���������̒B�������ǂ������ł��B�t�ɁA�ԈႦ����Ȃ�ł����Ȃ�́H�Ǝ��R�Ɍ��������ł��܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�P���������̉������ɂ��ā^18.12.04�n
X�|(3X�|2�j=�|11�@�̉��������킩��܂���B
�����Ă��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�h��̓�����q�˂Ă���ƍ���̂ŁC����ς��ē����܂��D
=-13)
�̏ꍇ
���ӂ�����


�萔���i���������̍��j���E�ӂɈڍ�����

���ӂ�

�̌W���Ŋ���
 …�i���j
…�i���j
�ǂ���肾��❤
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�O�����̒藝�ɂ��ā^18.12.03�n
�߂���߂���Q�l�ɂȂ�܂��I
��ς��肪�Ƃ��������܂��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[��Ԑ}�`�ƎO�����̒藝�ɂ��ā^18.12.01�n
enter�������Ɖł���悤�ɂ��Ă͂������ł����H
�����m��ҁn�F�A�����肪�Ƃ��D���̂��߂ɁH�uHELP�v��u���̖��v�Ƃ̑����̐����������Ȃ�����ƁC��舫���Ȃ�܂�
���m�ʂ̕ł���̎���ɑ���n[���̃O���t�ɂ��ā^18.11.30�n
��肪�����炭��̓I�ł͂Ȃ������̂ŋ�̓I�ɂ��Ăق���
�����m��ҁn�F�A�����肪�Ƃ��D���̃y�[�W�͑Ή��\�ɍi�������e�ɂ��Ă��܂����C�O���t�Ȃǂ́C�����Ɏ������T�u���j���[�Łu���ݒn�v�̑O��̃y�[�W�ɂ���܂��D�i����1366�h�b�g�C�c��768�h�b�g�̉�ʂŌ��Ă�����̂ŁC�T�u���j���[���\�������͂��ł��j
���m�ʂ̕ł���̎���ɑ���n[�S�����i�p�[�Z���g�j�ɂ��ā^18.11.29�n
�ƂĂ��킩��Ղ������ł��B
���ׂĂ̖��Ɏ����L�ڂ��Ă���Ə��悩�����Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�O�����̒藝�ɂ��ā^18.11.29�n
��肾�������ǂ���̂������œ��ӂɂȂ�܂���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�i���o�[�v���[�X�i�G���Ȃǂ̖��������j�ɂ��ā^18.11.29�n
�������o���Ăق���
���傤����5�N����o���Ăق���
�Ⴆ���b�g���≖�̖ʐ�
�����m��ҁn�F�A�����肪�Ƃ��D���w�Z�̋��ނɂ͌��o�����Ȃ��悤�ɂ��Ă��܂��D
���m�ʂ̕ł���̎���ɑ���n[�����̐����ɂ��ā^18.11.29�n
���肪�Ƃ�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���Ώ�,�_�Ώ́i�܂Ƃ߁j�ɂ��ā^18.11.28�n
���Q�i�S�j�̉���ŁA���x�Ђ͓��u�Ђ̊ԈႢ���Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�������������ϊ��ɂȂ��Ă��܂����̂Œ������܂����D����C���u�Б�̐H���Ńn���o�[�O��H�����������ɂȂ�܂����D
���m�ʂ̕ł���̎���ɑ���n[�Q�����̃O���t�ƒ����ɂ��ā^18.11.26�n
��S��㈡�̂R�ڂ̎��ɂȂ�l�����H���������Â炩�����ł�
���̑��̂��̂͂ƂĂ�������₷���đf���炵���ȂƎv���܂���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���E�����i�������j�ɂ��ā^18.11.26�n
�킩��₷�������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���ʊp�C���p�C�O�p�`�̓��p�̘a�C�O�p�̗��K����ɂ��ā^18.11.26�n
���������������ɂ��������ł��B
�������l�X�ȉ��p�����o���Ă����������肪�Ƃ��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝�ɂ��ā^18.11.26�n
�p�ꂪ�����킩��ɂ��������̂ŁA�p�ɐF��}(⚪�)�Ȃǂ��g���Ƃ����Ƃ킩��₷���Ȃ�Ǝv���܂�
�����m��ҁn�F�A�����肪�Ƃ��D��ABC�͉p��ƌ������͋L���ł��傤�D
���m�ʂ̕ł���̎���ɑ���n[�A���������̕��͑��ɂ��ā^18.11.25�n
1�̖��������̂ɑ��ēr������������}�X������������ǂ����̂ɂȂ�Ǝv���܂����B�Ȃ̂ŁA�A���P�[�g�ɏ������܂��Ă��������܂����B���ǂ����މ��P�Ɍ����Ċ撣���Ă��������B�킩��₷���đ��̂Ƃ͑S�R����ăq���g�Ȃǂ�����̂łƂĂ����₷���ł��B���̂悤�Ȃ킩��₷�����������Ă��������{���ɂ��肪�Ƃ��������܂��B�������A�Ԉ���Ă���Ƃ��ɖ��o�Ă����ł����ŏ��͂����Ă���̂��킩��Ȃ������̂ŏC�����Ă������������ł��B���̃A�C�f�A�ł����A�����N�}���~�̊Ŕ������ė����Ă���ȂǁE�E�E�����̓o���U�C�����Ă�������N�}�Ȃǂǂ��ł����H
�����m��ҁn�F�A�����肪�Ƃ��D���̋��ނ͍���Ă���20�N�߂��o�߂��Ă���C��ʍ\���Ȃǂ����̃X�}�z�Ή��ɂȂ��Ă��Ȃ��̂ŁC���낻���蒼���Ȃ���Ȃ�Ȃ��悤�ł�
���m�ʂ̕ł���̎���ɑ���n[�������ł������ɂ��ā^18.11.25�n
�𗧂��Ă���̂ł��炵���Ǝv���܂�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�_�Ώ̂Ȑ}�`�ɂ��ā^18.11.23�n
�ƂĂ�������₷��������܂���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝�ɂ��ā^18.11.23�n
�y����
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�P�����̕��͑��ɂ��ā^18.11.21�n
�ƂĂ�������₷���A������܂���😁���B����̂ł܂��͎����ʼn����Ă݂���Ă������Ƃ��ł��ėǂ������ł�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�ɂ��ā^18.11.21�n
�����Ɩ�萔�𑽂����Ăق����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�����Ɂu���ݒn�ƑO��̍��ځv�Ƃ������j���[��������̂ł����Ciphone�ł͓ǂ߂܂��H
���m�ʂ̕ł���̎���ɑ���n[�P���������̉������ɂ��ā^18.11.20�n
���������ʼn����̂ł͂Ȃ��L�[�{�[�h�őł��ĊԈႦ�Ă�����ǂ����Ԉ���Ă����̂����ӂ��������炢���Ǝv���B
�����m��ҁn�F�A�����肪�Ƃ��D�L�[�{�[�h������͂���y�[�W������܂��̂ŁC��������g���Ă�������
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝�ɂ��ā^18.11.20�n
�����ɊԈႢ�̊m�F���ł��邵�A����������̂łƂĂ��g���₷��
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������̕��͑��ɂ��ā^18.11.16�n
����ʼn������������Əڂ������ĉ�����
���������L��������������Ղ��Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�s�����̎g�����ɂ��ā^18.11.15�n
������ƂĂ�������₷���ł�!!
�e�X�g�ł́A���͖�������̂ŁA
���͖�肪����Ƃ����Ɨǂ��Ǝv���܂��I
(�s�����̖��ł�)
�����m��ҁn�F�A�����肪�Ƃ��D�s�����̕��͑���l���Ȃ��ẮI
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝(�������) �ɂ��ā^18.11.15�n
����t���Ȃ̂͗L���B������܂��B
�ȒP�Ȋ�{�̖�肪����Ƃ����Ə�����B
�����m��ҁn�F�A�����肪�Ƃ��D�㔼�̗v�]�̈Ӗ���������܂���DiPad���c�Ɏg���ƃT�C�h���j���[�������Ȃ��Ƃ������Ƃł����H
���m�ʂ̕ł���̎���ɑ���n[�O�����̒藝�ɂ��ā^18.11.14�n
�~���p���ق����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�ȗ����߂��ňӖ������m�ɓ`���܂��C�~���p�̒藝�̋��ނ��~�����ł��Ƃ����Ӗ��Ȃ�C���j���[������̂�����C���j���[�����ǂ���
�~���p�̒藝���������̂���Ȃ��ł����D
�O�p�̒�`�͂��ꂪ���߂��̂ł����H
�����m��ҁn�F�A�����肪�Ƃ��D�ǂ��̋��ȏ��ɂ������ĂȂ����Ƃ́C�o����K�v�͂Ȃ��ł��傤�D�Ƃ������C�L�j�ȑO����g���Ă���~�C���a�C�p�x�Ȃǂ̊T�O�ɂ��āC�����҂ɖ��O�����邩�ǂ�����������Ȃ��ł��傤�D
���m�ʂ̕ł���̎���ɑ���n[�~�ɓ��ڂ���l�p�`�ɂ��ā^18.11.12�n
�����������₷���Ă����Ǝv���܂��B�e�X�g�����Ŏ��ۂɐ�������������������ł��̎��ɍ̓_�ł���̂͂ƂĂ�����I���Ǝv���܂��B�����Ƒ�R�̖��������Ă݂����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
��?�m�͂ނ̂�����/��2�n�^18.11.11�n
���₷���킩��₷�������B
�ł��A1�����ς��Ă��܂�����A������x���邱�Ƃ��ł��Ȃ����ĂƂ��낪�c�O�ŕs�ւ��Ǝv�����B
�����m��ҁn�F�A�����肪�Ƃ��D�ǂ̃y�[�W�̂��Ƃ��������Ȃ��ƁC�b���ʂ��܂���D
���m�ʂ̕ł���̎���ɑ���n[�P�����̕��͑��ɂ��ā^18.11.11�n
�g���₷���I���̈ꌾ�ł��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝�ɂ��ā^18.11.11�n
�������킩��₷�������ł��B
�����Q�l�ɂ����Ă��������܂��I
���̓�Փx�����������グ�Ă��������Ă������Ǝv���̂ŁA���ꂩ������҂��Ă��܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�O�p�`�̖ʐ��ɂ��ā^18.11.06�n
�F�X�Q�l�ɂȂ邱�Ƃ����X����A���肪�Ƃ��������܂��B����������ɔY��ł���܂������������������������܂��B�ӎO�p�`�̈�ӂ�6�p�œ��p��30���̖ʐς����߂�Z����肪�������ɍ����Ă���܂������Ē����܂��悤���肢�v���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�ӎO�p�`�̈�ӂ�6�p�œ��p��30���Ƃ��������ł�4�ʂ�̌`������C���Ă����߂��܂���D�܂��C��������Z�����ł͂Ȃ��C���Ȃ��Ƃ��O�����̒藝���O�p�����K�v�ł��傤�D
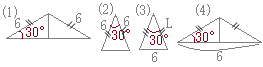
(1) �ӂ�6cm�ŗ���p��30���̏ꍇ�F

(2) �ӂ�6cm�Œ��p��30���̏ꍇ�F

(3) ��ӂ�6cm�Œ��p��30���̏ꍇ�F�]���藝�ɂ��

)
(4) ��ӂ�6cm�ŗ���p��30���̏ꍇ�F

(�R)��
�������BAT�L��90���́A����ł����ǁA����Ȃ��Ƃ�������ł����B
(73�˖��E�j)
�����m��ҁn�F�A�����肪�Ƃ��D�Ȃ������v���̂ł����H
���m�ʂ̕ł���̎���ɑ���n[�H�����̔Z�x�ɂ��ā^18.11.03�n
���肪�Ƃ��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���̃O���t�ɂ��ā^18.11.02�n
���W�̏������������Ă��炢�����ł��B
�ł��A�������킩��₷���Ă���ȊO�́A�킩��܂����B
�����m��ҁn�F�A�����肪�Ƃ��D���W�̏�������
���̃y�[�W�����Ă��������D
�ƂĂ�������₷�����K�ɍœK�ł����B�����������₷�������ł�
���肪�Ƃ��������܂���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�O�p,���p�`�ɂ��ā^18.10.29�n
���ɂȂ����A������������A�������Ă��炦����A�������̂����A
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���̃O���t�ɂ��ā^18.10.26�n
���̃O���t�́����ɂȂ聛�̓_��ʂ�
�킩��܂����Ă�������
�����m��ҁn�F�A�����肪�Ƃ��D�ǂ̏o�ŎЂ̋��ȏ��ł��C�O���O���ɑ��g�ň͂�ŏ����Ă����ˁD�Z�̓_�ł͂Ȃ�����ǁD
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝�ɂ��ā^18.10.26�n
�ƂĂ�������₷�������ł��B���肪�Ƃ��������܂�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���̒l�ɂ��ā^18.10.22�n
�� �� �� �� �� �B�B�B
�����m��ҁn�F�A�����肪�Ƃ��D�����Ƌ�̓I�ɏ����Ȃ��ƁC���ꂾ���ł͎肪����������Ȃ��̂ŁC�����悤���Ȃ��ł��D
���m�ʂ̕ł���̎���ɑ���n[���Ώ�,�_�Ώ́i�܂Ƃ߁j�ɂ��ā^18.10.22�n
���肪�Ƃ�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Ă��ɂ��ā^18.10.17�n
�d��̏d�������łȂ��A�x�_����̋��������߂��肪����ƂȂ��ǂ��Ǝv���܂��I�I
�����m��ҁn�F�A�����肪�Ƃ��D������͂����Ă��悢���C���������܂��Ă��Ȃ���C�G�ɂ͂ł��Ȃ��̂���_
���m�ʂ̕ł���̎���ɑ���n[�Β��p,���ʊp,���p�ɂ��ā^18.10.17�n
������������𑝂₵�ė~�����ł��B
���ƁA���Ȃǂ����ĂЂƂ߂ŕ�����悤�ɂ��Ăق����ł�
�����m��ҁn�F�A�����肪�Ƃ��D����ȏ�H
���m�ʂ̕ł���̎���ɑ���n[�ꎟ�������i�������ƌ��Z�̎d���j�ɂ��ā^18.10.16�n
�����Ă�����Ă�������Ȃ�����ǂ������番����܂����H
�����m��ҁn�F�A�����肪�Ƃ��D����N�ɋ����Ă�����āC�ǂ��̕������ǂ�������Ȃ��̂�������Ȃ���…���̃y�[�W�̂悤�Ȗ�������Ă�������Ȃ��ƌ����Ă�����̂ł�����C�₳������肩�班���������Ƃ悢�ł��傤
���m�ʂ̕ł���̎���ɑ���n[�A���������̍���������͑��ɂ��ā^18.10.16�n
�����̏������̍s�ƕ������d�Ȃ��ĂČ����ɂ����̂ł����������Ԃ��J���Ă����Ɗ������ł�
�����m��ҁn�F�A�����肪�Ƃ��D�����J���܂����DAndroid��Chrome��PC�p�̃y�[�W��ǂ�ł�����悤�ł����C�X�}�z�p�͕ʂɍ���Ă��܂��D
���m�ʂ̕ł���̎���ɑ���n[���s���Ɗp�ɂ��ā^18.10.16�n
�}�������Ă���̂��ʔ��������ł���I�I�S�ē������Ă݂��炢���Ǝv���܂����I�I�I�F�B�̂W�X�D�Q�U�R�T�S�������������炢���Ǝ^�����Ă���܂�����I���ɗF�B�̍�������(����)�͓������ق����y�������ɓ���ƌ����Ă����܂������I�悩�����ł���ˁI�I�I���ЁA�킽���������̈ӌ���������Ă��������܂��悤�A��낵�����˂����������܂��B�@�k�C���ݏZ(��)�@�H�R�@�P��(�y���l�[��)���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝�ɂ��ā^18.10.11�n
�킩��₷���ł��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������ɒ������K�ɂ��ā^18.10.10�n
���Z�̏����ŕ\���܂��傤�Ƃ���̂ł����A��邩���A����鐔
�ǂ��炪����A���q�ɂ���̂ł����H
�����m��ҁn�F�A�����肪�Ƃ��D�����ɁC�i�d�v�F���q�������鐔�C���ꂪ���鐔�ł��j�Ə����Ă���܂��D���́u�d�v�v�Ƃ��������������Ƃ������Ƃ炵���̂ŁC�����Ɩڗ��悤�ɂ��Ă����܂��D
�@�����w���̊ԂɁC���̎�������āC�^����������Ă������Ƃ���ł��D�����̐��k�ɂƂ��ẮC���̘b�͓��R�̂��ƂȂ̂ŁC���́u�d�v�v�Ƃ�������傫�������߂���ƁC�n���ɂ���Ă���Ǝ~�߂�ꍇ������C��舵���͐T�d�ɂ��Ȃ���Ȃ�܂���D�����C���Z���ł��t�Ɏv������ł��鐶�k�͂��܂ɂ��āC���N������Ă��܂��Ă���ƁC�����ɂ����̂ł��D
���m�ʂ̕ł���̎���ɑ���n[�Q�_��ʂ钼���̕������ɂ��ā^18.10.10�n
�q���g�ʼn��������o�Ă��邩�番����₷���Ƃ��Ă悩����
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������ƒ����i���ĕt:���j�ɂ��ā^18.10.9�n
�ǖ₠�肪�Ƃ��������܂��B�y�R��(o_ _)��))
(�Q)�̖��ŁA���{��̕��@�Ƃ��āu�`�Ƃ���Ƃ��v�Ƃ����\�L�������Ă����_�������C�ɂȂ����̂ŁA
���_��O�Ƃ���Ƃ��A�_B��ʂ����AB�ɕ��s�Ȓ�����x���Ƃ̌�_��F�Ƃ���B
���̎��A�_F�̍��W�����߂Ȃ����B
�Ƃ������`�ɂ�����悢�Ǝv���܂��B
���̂ق��͂ƂĂ��f���炵���Ǝv���̂ŁA���ꂩ����撣���Ă��������B
�������炵�܂����io_ _)���j�j
�����m��ҁn�F�A�����肪�Ƃ��D�������܂����D
���m�ʂ̕ł���̎���ɑ���n[�_�Ώ̂Ȑ}�`�ɂ��ā^18.10.9�n
��������������₷��
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[��i�@�ɂ��ā^18.10.8�n
��i�@�����ł��܂��o�����Ă��Ȃ������̂ł����A���̃y�[�W��ǂ�ŗ������邱�Ƃ��ł��܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Q�_�Ԃ̋����̌����ɂ��ā^18.10.8�n
����ɂ��́B�R�����g���炵�܂��B�O�����̒藝�͒��p�O�p�`�ł����g���Ȃ����ǁA�Q�_�Ԃ̋����͒��p�O�p�`�ȊO�ł��g���܂���??
�����m��ҁn�F�A�����肪�Ƃ��DYes, No�����œ�����̂Ȃ�CYes�ł����C�����������₪�ς���Ȃ����ȁD2�_�ł͎O�p�`���ł��Ȃ�����C���p�������O�p�`���Ȃ��D�i���ꂪ�\�����̓��j
�i�������̓��j���̃y�[�W�ɏ����Ă���悤�ɁC2�_�Ԃ̋����̌����͒��p�O�p�`�������ďؖ�����̂ŁC���p�O�p�`���g���D
���m�ʂ̕ł���̎���ɑ���n[�ω��̊����ɂ��ā^18.10.7�n
You are great! I love this site!!! Thank you very much.
I'm 51years old. I'm learning from you a lot.
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������ɒ������K�ɂ��ā^18.10.7�n
�����̏o���Ȃ��Ƃ��낪�ǂ�������܂����B���肪�Ƃ��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�P���������̕��͑�i���ĕt:���j�ɂ��ā^18.10.6�n
���ȏ��Ƃ��ɏo�Ă�����Ƃ�������Ȃ̂Ńe�X�g���ɂȂ��Ă����Ǝv���܂��B�@��1�j�q���
�����m��ҁn�F�A�����肪�Ƃ��D�悢�]�������Ă�����Ă���̂ŁC�f���ɂ��肪�Ƃ��ƌ��������̂ł����C���e�҂Ɖ҂������ǂ�ł��邾���łȂ��āC���J���Ă���ꍇ�ɂ́C���̐��Ƃ��ǂޏꍇ������̂ŁC�����Ȗ�肪�܂܂��ꍇ������܂��D�u���ȏ��Ƃ��ɂ�������v�ƂȂ�ƁC���쌠�͂ǂ��Ȃ��Ă���̂��Ƃ�����肪��������̂ł��D����ɂ��ẮC���ȏ��̃��x���͍l�����܂����C�����̓R�s�[���Ă��܂���Ɠ����܂��D���́C���̃y�[�W�͂ƂĂ���J���č�������̂ŁC�����̕����͂��ׂăv���O�����Ő������Ă��܂�…���C����C���͊Ǘ��l�����߂����̂łȂ��C���̎��X�ɗ����I�Ɍ��߂Ă��܂��D
���m�ʂ̕ł���̎���ɑ���n[�������̍����ɂ��ā^18.10.1�n
�����Ɠ�������p�ӂ��Ăق��������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D���̃T�u���j���[�Ɏ�����**�������̕��͑�**�Ƃ������ڂ̒��ŁC��ԊȒP�ȍ��ڂ�����Ă��邩��C�ȒP�Ȃ̂ł��D���̍��ځC���̎��̍��ڂ����Γ���Ȃ�܂��D
���m�ʂ̕ł���̎���ɑ���n[�����v�Z�i�j�ɂ��ā^18.9.30�n
�ׂ��������܂ŏ�����Ă��ĂƂĂ�������₷�������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Q���������̉������i�܂Ƃ߁j�ɂ��ā^18.9.30�n
���ɗ������I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�O�p�`�̖ʐς̓����ɂ��ā^18.9.30�n
�_�n��ʂ�Ȃ��O�p�`�̖ʐς�2�����͂ǂ��������ł����H
�����m��ҁn�F�A�����肪�Ƃ��D����̈Ӗ����ʂ��܂���D…���Ԃ̖��̘b�Ȃ̂��C�_�n��ʂ�O�p�`�̖ʐς�2�����Ƃ������͂ǂ��ɂ���̂�
���m�ʂ̕ł���̎���ɑ���n[�O�p�ɂ��ā^18.9.30�n
�|�C���g�̕����������Əڂ������Ăق����ł�
�����m��ҁn�F�A�����肪�Ƃ��D�����|�C���g�ł��邩�́C�e���̊w�K�̐i��ɂ���ĕς��܂����C���Ȃ��̏ꍇ�͂��Ԃ�C�ڎ���
���̍�����ǂނƂ悢�ł��傤�D
���������킩��₷��!
����ł��A�܂Ƃ߂Ă��炦��ƁA�����Ɨǂ��ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[ �~�ɓ��ڂ���l�p�`�ɂ��ā^18.9.29�n
������ƂĂ��킩��₷���ĎQ�l�ɂȂ�܂��B���肪�Ƃ��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������̕��͑�i���̗��K�j�ɂ��ā^18.9.28�n
�ςɌł��l����Ə�������ł����B��������ƕ��͂�ǂނƊȒP�ɉ����܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�H�����̔Z�x�ɂ��ā^18.9.28�n
���̗l�ȃc�[�������邱�Ƃ����߂Ēm��܂����A���S�҂ɂƂ��Ĕ��ɗ������₷�����ނƂȂ�܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���ލ����܂Ƃ߂��ɂ��ā^18.9.27�n
�����ƕ�����₷���Z���������Ăق���
�����m��ҁn�F�A�����肪�Ƃ��D����ȏ�͖����ł��D�d�����i����i���w�������Ƃ��ł��C���̒��x�̒Z�������������ǂ߂Ȃ���C���퐶�����s�ւɂȂ�܂�����C�����悤�ɂ�������悢�ł��D
���m�ʂ̕ł���̎���ɑ���n[�O�p�ɂ��ā^18.9.27�n
�ƂĂ�������₷�������ł�
�O�p�̒�`�������܂��ɂȂ��Ă����̂ł��̋L�����݂ė������邱�Ƃ��ł��܂���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������̕��͑��ɂ��ā^18.9.26�n
1��140�~�̃P�[�L��350�~�̃P�[�L140�~�̃P�[�L���3�����Ȃ�悤�ɔ������Ƃ��덇�v��4480�~�ɂȂ�܂����B2�̃P�[�L�͂��ꂼ�ꉽ�����܂������H
�����m��ҁn�F�A�����肪�Ƃ��D�����ƁC���̋��ނ�ǂ�ł��̎��₪����Ƃ������Ƃ́C���̋��ނ�����ĉ����g�ɒ����Ȃ������Ƃ������ƂɂȂ�܂��H���Ղɓ������������߂�ԓx�͋^��ł��D�����̓r���o�߂������܂��傤�D
���m�ʂ̕ł���̎���ɑ���n[�_�Ώ̂Ȑ}�`�ɂ��ā^18.9.25�n
�Z���D���̘V�l�ł��B��ς킩��₷���Ă������낢����ł����B�����A�_�Ώ̐}�`�̐����Ƃ��āA�u�Ώۂ̒��S��ʂ钼���Ő�ƁA�ʐς͕K���������B�v�Ƃ����̂��Ȃ��̂ŏ����s���ł��B
���̂��Ƃ́A�����Ƃ��Ēf�����邾���ł����̂��ǂ����A�܂�ʐς͕K��������闝�R����������[�������闝�����K�v���ǂ�����������܂���B�i�ؖ��̕K�v���̗L���j�_�Ώ̗��̐}�`�̂Ƃ��A�u�Ώۂ̒��S��ʂ镽�ʂŐ��(�ؒf����Ɓj�̐ς͕K���������B�v�͂ǂ�����Ĕ[���������炢���ł��傤���B��낵�����w�쉺�����B
�����m��ҁn�F�A�����肪�Ƃ��D���w�Z1�N���̓_�Ώ̂Ƃ��Ắi���j�Ώ̂Ƃ̈Ⴂ�������邱�Ƃ��K�v���\���ȖڕW�ł��傤�D�ɍ��W�ł̖ʐς̋��ߕ��͍��Z���w�V�ōl����ꍇ������܂����C���ȏ��ł͈������Ԃ͂Ȃ��ł��傤�D�������Ƃ��Ă͂��肦�܂��D
���m�ʂ̕ł���̎���ɑ���n[1�����ɂ��ā^18.9.25�n
�ƂĂ��킩��₷���ǂ������ł�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�P���������̉������ɂ��ā^18.9.23�n
�悭������܂���
�����m��ҁn�F�A�����肪�Ƃ��D���̋��ނ̊Ǘ��l�͂��Ȃ��̎��_�ł͂���܂���D���Ȃ������܂łǂ�Ȋw�K�����Ă��āC���̋��ނɂ��āC�ǂ̉ӏ����ǂ�������Ȃ������q�ׂȂ�����C�����悤������܂���D�Œ�ł��C���{�l�Ȃ̂��C���w���Ȃ̂��C�w�Z�ɂ͍s���Ă���̂��������Ȃ��ƁC�b�����藧���܂���D
���m�ʂ̕ł���̎���ɑ���n[�����i�S����,����,�����j�ɂ��ā^18.9.21�n
500����70�p�[�Z���g�̏d���́H
�����m��ҁn�F�A�����肪�Ƃ��D���̃y�[�W��ǂ��ʂƂ��āC���̎��₪����̂��H����͂܂�C���������ł��Ȃ������Ƃ������Ƃł͂Ȃ��̂��H
���m�ʂ̕ł���̎���ɑ���n[�P�����̕��͑�i���ĕt:���j�ɂ��ā^18.9.19�n
�������ł����B�ƂĂ��Q�l�ɂȂ�܂����B���肪�Ƃ��������܂����I
�����m��ҁn�F�A�����肪�Ƃ��D���̃y�[�W��J�߂Ă����̂́C�m�I�����������ڂ̐��k���Ǝv���D�i�Ȃ��������v���j
���m�ʂ̕ł���̎���ɑ���n[�A���������̍����ɂ��ā^18.9.5�n
���̉��ɂ��̖��̓������ڂ��Ă���Ă��珕����܂��B
�����m��ҁn�F�A�����肪�Ƃ��D���̃y�[�W�́C�A���������̍����̃y�[�W�ł��D�������K�v�ł�����������̉������̃y�[�W�����Ă��������D
���m�ʂ̕ł���̎���ɑ���n[�P�����Ƒ������ɂ��ā^18.9.4�n
�����̌�ɗ��K��肪�����āA�ƂĂ��ǂ������ł��B�P�����Ƒ������̈Ⴂ�ɂ��Ă悭������܂����B�ق��̃T�C�g�ɂ͍ڂ��Ă��Ȃ������AX����1�͒P�����ł��������ł������Ƃ����̂������āA�ǂ������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������ɒ������K�ɂ��ā^18.9.2�n
������₷���ėǂ��ł��I�I�X�X���ł��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�P���������̉������ɂ��ā^18.9.2�n
�y���߂܂���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�O�p�ɂ��ā^18.9.1�n
���������A���̏�ō̓_�A�q���g�����炦�āA�ƂĂ��������ɂȂ�܂����B
�L��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�i���o�[�v���[�X�ɂ��ā^18.8.31�n
������ɒ�܂���ł����Ă����߂��Ȃ��ӏ�������ƕ\�������
�����m��ҁn�F�A�����肪�Ƃ��D���������Ȃ���C����1�ɒ�܂�Ƃ͌����܂���D
���m�ʂ̕ł���̎���ɑ���n[�s�����̎g�����ɂ��ā^18.8.30�n
���肪�Ƃ��������܂��B
�@����������ɂȂ�Ȃ����I
�@�@�ł������ĂȂɂ����
���̂ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D�O���Łu���ɂȂ�܂����v�Əq�ׂĂ���̂�����C����ł����̂���Ȃ���
���m�ʂ̕ł���̎���ɑ���n[��`�̖ʐ��ɂ��ā^18.8.26�n
�ƂĂ��킩��₷���Q�l�ɂȂ�܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����`�̕������ɂ��ā^18.8.26�n
���ӂ̕����x�����������̏ꍇ�͂ǂ̂悤�ɉ��������̂ł����H
�����m��ҁn�F�A�����肪�Ƃ��D���̃y�[�W�͒��w�������̋��ނł��D���w�������ɕ���ɂ����Q�����Ă���������̖��͏o�܂���D���̎���͍��Z�������̃y�[�W����Ȃ炠�蓾�܂��D
&chf=bg,s,fff6f6)
�̂Ƃ��C

…(1)�Ƃ��ė��ӂ̕������
x=0&chf=bg,s,fff6f6)

�̂Ƃ�

�����(1)�ɔ����邩����Ȃ��D

�̂Ƃ��C�Ⴆ��

�̂Ƃ��́C

�ƂȂ邘�͉��ł����D
�@���Z�Ȃ�C�����������̖��Ƃ��āC���̂悤�Ȗ����o�܂��D


…(1)�Ƃ��ė��ӂ̕������



������ڂ����ĂƂĂ��Q�l�ɂɂȂ�܂���😆
�������A�����ȒP���Ǝ��͊������̂ł���������Փx�̍��������f�ڂ��Ăق����ł�
��낵�����肢���܂�🙇��
�����m��ҁn�F�A�����肪�Ƃ��D��{���͂₳�����ł��D���j���[�Ŏ��̃y�[�W�ɐi�ނƓ�����ɂȂ�܂��D
���m�ʂ̕ł���̎���ɑ���n[���߂��P���s��(1.1)�ɂ��ā^18.8.23�n
77�ł��킩��₷���B���Ɉӗ~���N���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D���̃y�[�W�͍ŋ߂̍�i�ŁC�ǂ������Ă���̂��C�C�ɂȂ��Ă��܂������C�悢���̊��z�Ǝ��܂����D
�u�ł��v�͕t���Ȃ��Ă��悢���ƁD…�\�̈ʂ܂Ŏ��t���āC�l�̌ܓ��̎d�����H�v����ƁC�Ǘ��l�Ɠ���
���m�ʂ̕ł���̎���ɑ���n[�A���������̉������i����@�j�ɂ��ā^18.8.21�n
�� x���� y �]�@
��x���� y+�� �]�A
���̌`�̑���@�̂����������ė~���������ł�
�����m��ҁn�F�A�����肪�Ƃ��D
��x����y �]�@
��x����y+�� �]�A
�̂����Ƃ������̂����ʂɂ���ƍl���邱�Ƃɖ���������܂��D����Ȃ��̂��̂܂Ŋo����K�v�͂Ȃ��̂ł�
��x−��y=0 �]�@
��x−��y=�� �]�A
�ɒ����Ή������𑝂₳�Ȃ��čςނ̂ł��D
�����ɋ߂Â��Ă��������������͂ɂ��Ăق����ł�
�ق��͖𗧂��܂��� ���̒��q�ō��x�̖͎����撣�ꂽ��Ǝv���܂�
�����m��ҁn�F�A�����肪�Ƃ��D���̃y�[�W�ł́C���͑�̕����ˑ����i�����̘b�Ȃ番���邪�C���x�̘b�ɂȂ�ƕ�����Ȃ��Ȃ�Ȃǁj�Ɋւ��āC�������ɂ����猋�Ǔ����Ȃ̂��Ƃ������Ƃ�[�����Ă��炤���Ƃ�ڕW�ɂ��Ă��܂��D
���m�ʂ̕ł���̎���ɑ���n[�Q�_��ʂ钼���̕������ɂ��ā^18.8.16�n
�������킩��₷���ł��B
�w�Z�̋����Ȃ�������ۂǗǂ������ł��B
�����̌�̖��1���ƂĂ��ǂ������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�l���v�Z�̗D�揇���ɂ��ā^18.8.14�n
5�~3+(5-3)7��7�͎w��
�������悤�Ȏ����������ꍇ�A�ǂꂩ���Ɍv�Z��������̂ł����H
�����m��ҁn�F�A�����肪�Ƃ��D���̋��ނɏ����Ă���ʂ�ɂ��ł��܂�.
^7&chf=bg,s,fff6f6)
�̏ꍇ�C(�T)�������̒���(�U)�ݏ恨(�V)�揜��(�W)�a���̏�������
\rightarrow 5\times 3%2B 2^7\hspace{10}(II)\rightarrow 5\times 3%2B 128&chf=bg,s,fff6f6)
\rightarrow 15%2B 128\hspace{10}(IV)\rightarrow 143&chf=bg,s,fff6f6)
���Q��{���|3=0
�̓���
�����m��ҁn�F�A�����肪�Ƃ��D
���̌������ɕ����܂��傤�i�������߂�v���O�����ɐ������������ށj
���4����ȍ~�A�}�̎w�肪�ЂƂ���Ă���
�����m��ҁn�F�A�����肪�Ƃ��D�������܂����D
���m�ʂ̕ł���̎���ɑ���n[�����̕ό`�ɂ��ā^18.8.9�n
�����Ɠ�������o���Ăق����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�u�悭�킩�����̂ŁC�����Ɠ�����ł����ӗ~���o�Ă����v�Ƃ������C�̕��܂܂�Ă��邱�Ƃ͕�����܂��D�����C���Ȃ��Ɍ��炸�X�}�z�ǎ҂̓����Ƃ��āu���̃y�[�W�ɂ��ׂĂ̏������Ă��Ȃ���Ȃ�Ȃ��v�Ƃ����v�����݂͂Ȃ��̂��H�@�艺���Č����C���w�͓_�v�l�ł͂Ȃ��C���Ƃ��ĂȂ��āC�ʂƂ��čL���čl����Ȃ���̊w��i�W�̊w��j�Ȃ̂ŁC�_�v�l�͂悭�Ȃ��ƍl���܂��D
�����Ɠ�����́C���j���[�̎��̃y�[�W�����邾���ŏo�܂��D
���m�ʂ̕ł���̎���ɑ���n[�l���v�Z�̗D�揇���ɂ��ā^18.8.8�n
�ƂĂ�������₷�������ł��B���肪�Ƃ��������܂����I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����`�̕������ɂ��ā^18.8.7�n
�N�}�̕\�������Ȃ��������������ƏΊ�ɂȂ�Ƃ����Ă��ꂽ�番����₷���������ȁB
�Ȃ�Ƃ������A�A�A�����ƕ|���\��������琳�����������ԈႦ���Ǝv���Ă��܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�ǂ��炩�Ƃ����ƁC���̋��ނ̍�҂͗��Ȍn�ŁC�G�����ӂł͂Ȃ�…���w�Z�̐}��H��̐��т́C����3���炢���������ȁD
�����C���̏�ʂ́u�ɂ�������v�Ƃ���������\�������̂ł͂Ȃ��C�F�̂����肳�CVIP���̐l���ʂ����Ƃ��Ɍh�炵�Ă��銴����\��������ł��D
���m�ʂ̕ł���̎���ɑ���n[�Q���������̉������i�܂Ƃ߁j�ɂ��ā^18.8.6�n
x2=x �͔@�������Ηǂ��̂ł����H
�����m��ҁn�F�A�����肪�Ƃ��D(B)���������ł�����͈̂��������ʼn����̂��悢����C
=0&chf=fffff3)

���������b�ɂȂ��Ă���܂��B�l�p�`�̊O�S���l�p�`�̊O�܂�l�p�`�����a�̏㔼���܂��͉������łS�_�����邱�Ƃ͂Ȃ��̂ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D���ɕς�������ƂłȂ��C���ʂɂ���܂��D���2�C���4�̐}�͂��傤�ǒ��a��ł�������������������点��ƁC�����Ȃ�܂��D�i���ۂɂ́C�ǂ�Ȏl�p�`�ł��O�S������킯�ł͂Ȃ��C3�_�ŊO�ډ~�����܂�̂ŁC4�ڂ̒��_�͂��̉~����Ɏ��Ȃ���Ȃ�܂��C4�_�Ƃ����~�̈�����ɂƂ�C�����Ȃ�܂��j
���m�ʂ̕ł���̎���ɑ���n[�A���������̕��͑�2�ɂ��ā^18.8.2�n
�r�̖��o��
�����m��ҁn�F�A�����肪�Ƃ��D���t���������\�Ȃ̂ŁC�ʏ�͉��Ȃ��̂ł����C�Q�l�܂łɁD�u�r�̖��v�ł͘b���ʂ��܂���D�����̂���Ă���h��ɂ͉��Ə����Ă��邩�킩��܂��C���{�����ɂ���Œʂ���l�͂��Ȃ��ł��傤�D
���������āC�o��^���l�Z�̂��Ƃ������Ă���̂��ȁH
���m�ʂ̕ł���̎���ɑ���n[�P���������̉������ɂ��ā^18.8.1�n
6=�w����18
�����m��ҁn�F�A�����肪�Ƃ��D����Ȃ玿��ƁC�ӌ��Ȃ�ӌ��Ə����Ȃ�����߂ł��D���ꂾ�����ƒʂ肪����̂�������ɐ���𓊂��Ă���悤�Ȃ��̂ł��D

�̗��ӂ�

���|���ĕ����

���ӂ��U�Ŋ���

���܂ŋ�����Ƃ��߂ɂȂ�Ȃ��̂ŁC���Ƃ͎�����
�~���p�̒藝��2�̗�̐�������
��BCD=2�~��BCO�́A�����炭��BCO=2�~��BCD���Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�m���ɂ��������Ƃ��낪�������̂Œ������܂����D�����C���Ȃ��̐��������ɂ���Ă���Ƃ��낪����܂��D
���m�ʂ̕ł���̎���ɑ���n[�f���������̉��p�ɂ��ā^18.7.31�n
�ƂĂ�������₷��������肪�Ƃ��������܂���‼︎
���̂��Ƃ����Ė����������Ƃ��ł��e�X�g�ɔ����ꂽ�C�����܂�
�{���ɂ��肪�Ƃ��������܂���‼︎
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���Ώ̂Ȑ}�`�ɂ��ā^18.7.30�n
�f���炵���I�����ł��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���̂̕\�ʐ�.�W�J�}�ɂ��ā^18.7.30�n
2.3 �O�p���̕\�ʐ�
�c��̗����̂̕\�ʐ�
S�Q��3�~3�~1/2+��BDE+3�~3�~3
S2�[S 1��27
���Ǝv����ł����B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂���
���m�ʂ̕ł���̎���ɑ���n[���ލ����܂Ƃ߂��ɂ��ā^18.7.29�n
���肪�Ƃ��������܂����B�悢�Q�l�ɂȂ�܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Q�������� (x+a)2=A �̉��ɂ��ā^18.7.26�n
�R���Q��|���|1�̂����������Ă�������
�����m��ҁn�F�A�����肪�Ƃ��D2���� �R���Q��|���|1��2���������R���Q��|���|1��0�̈Ⴂ�ɒ��ӂ��܂��傤�D
���̃y�[�W�̉��̕��ɖ����������ނƓ������o�܂��D�������C-x��(-1)x�Ə����D
�ƂĂ����₷��
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�P�����Ƒ������ɂ��ā^18.7.23�n
3x-2y�͉������ł���
�����m��ҁn�F�A�����肪�Ƃ��D3x��1������2y��1�����Ȃ̂ŁC�����̍������i�������ꍇ���悢�j�łP�����ł��D
���m�ʂ̕ł���̎���ɑ���n[���Ώ̂Ȑ}�`�ɂ��ā^18.7.22�n
�f���炵���I�����ł��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�ɂ��ā^18.7.22�n
�߂����Ⴑ�[��[��y�ɉ������肪����Ɗ������ł��B✨
���p�Ƃ��̉������Ȃǂ�������Ē�������������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D���p���̓T�u���j���[�ł����ƌ��̖���I��ł��������D��������HELP�ŏo�܂��D
���m�ʂ̕ł���̎���ɑ���n[�������ɒ������K�ɂ��ā^18.7.21�n
���肪�Ƃ��������܂�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���̐��w�ɂ��ā^18.7.18�n
�ǂ��ł��I
�����m��ҁn�F�A�����肪�Ƃ��D38���C39���ɂȂ�ƁC�N�[���[�������Ȃ��āC�o�b���_�E�����Ă��܂��č�Ƃ��ɂ����D�Ƃق�
���m�ʂ̕ł���̎���ɑ���n[�ŏ����{���̉��p����ɂ��ā^18.7.10�n
����������������o���ĉ������B
�����m��ҁn�F�A�����肪�Ƃ��D���w�Z�̖��Ȃ̂�…
���m�ʂ̕ł���̎���ɑ���n[�������ɒ������K�ɂ��ā^18.7.07�n
1.05�͂ȂɂԂ�̉��H
�����m��ҁn�F�A�����肪�Ƃ��D(7)�̏�ɏ����Ă���܂��D

�������킩��₷���ł��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����̉��p.�Ă��̌����ɂ��ā^18.7.06�n
�����͂����߂�ȊO�ɁA���������߂�������肢���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�v�]�̈Ӗ��͕�����܂����C���̏������������
���m�ʂ̕ł���̎���ɑ���n[�����̕ό`�ɂ��ā^18.7.06�n
����ȊO�Ƀ��[�g�̕ό`�̖�肪�ł���T�C�g���Ȃ������̂Ŋ������ł��B����������肪������Ί������ȂƎv���܂��I
�����m��ҁn�F�A�����肪�Ƃ��D�y�[�W�̐擪�ɂ���T�u���j���[�ŁC�m���ݒn�n�ƕ\�����Ă���܂��悤�ɁC���Ȃ����ǂ͍̂����Ɋւ���20�y�[�W�قǂ���y�[�W�̂����̂P�y�[�W�ł��D�S�����Ƃ͌����܂��C���ʂ͏\������Ǝv���܂��D
���m�ʂ̕ł���̎���ɑ���n[�O�ӂ̒������^����ꂽ�O�p�`�ɂ��ā^18.7.05�n
�e�X�g�O�ŁA���������ɗ����܂����I
���肪�Ƃ��������܂��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[����ɍ����̂Ȃ��`�ɂ��ā^18.6.29�n
���P�i�S�j�̐ݖ₪�i�R�j�Ɠ����ɂȂ��Ă��܂��B����ł̓��[�g�̒���2/3�������ۂ�����Ă��܂��B���������肢���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂����D
���m�ʂ̕ł���̎���ɑ���n[�A���������i�����@�j�ɂ��ā^18.6.28�n
�ƂĂ��ǂ��Ǝv����
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������g�������ɂ��ā^18.6.28�n
�e�X������܂�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�P���������y a�̒l �z�ɂ��ā^18.6.28�n
�����������킩��ɂ����ł�
�����m��ҁn�F�A�����肪�Ƃ��D���̃y�[�W���C�ԐM���ꂽ�ޗ��ʼn��P����͖̂����ł��D���̃y�[�W�����邩�C������x���ȏ���ǂݒ������C�������������ōl���Ă��������D
���m�ʂ̕ł���̎���ɑ���n[�P�����̌v�Z�ɂ��ā^18.6.27�n
�����Ɠ������������ė~�����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D����ɃT�u���j���[������܂��̂ŁC���̌v�Z�C���̒l�C���͑�Ɛi��ł��������D
���m�ʂ̕ł���̎���ɑ���n[�Q���������̉������i�܂Ƃ߁j�ɂ��ā^18.6.27�n
�悭������܂���B��������������₷�������ĉ������B
�����m��ҁn�F�A�����肪�Ƃ��D���̃y�[�W�͂܂Ƃ߂̃y�[�W�ł��D�܂Ƃ߂̃y�[�W����ǂނ̂ł͂Ȃ��C�����ƑO�̕��i��ɂ���T�u���j���[��x2=a�ɂ��������j����ǂ݂܂��傤�D
���m�ʂ̕ł���̎���ɑ���n[�������������ƂȂ邎�̒l�ɂ��ā^18.6.27�n
�������悩�����ł�������܂����A
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������ɂ������ɂ��ā^18.6.27�n
�������Ă�̂��悭�킩��Ȃ������Â炢
�����m��ҁn�F�A�����肪�Ƃ��D������B���ɂ������悤�ɂ��܂��傤�D�u�^��������v���Ƃ���X�^�[�g����Ɗy�ł�=�Տ��̊����ŁD
���m�ʂ̕ł���̎���ɑ���n[�ω��̊����ɂ��ā^18.6.27�n
(9)�̉���ł����Ax���`�̂Ƃ�y���`�ƂȂ�͂��̂Ƃ��낪�A�����Ƃ�x�ɂȂ��Ă��܂�
�����m��ҁn�F�A�����肪�Ƃ��D�������܂����D
���m�ʂ̕ł���̎���ɑ���n[�A���������ɂ��ā^18.6.26�n
���m�ʂ̕ł���̎���ɑ���n[�ڌ��藝�ɂ��ā^18.6.25�n
�ʂ̎����Ԉ���Ă܂�
�����m��ҁn�F�A�����肪�Ƃ��D�����ƁC�Ǘ������ɂȂ��Ă��܂����̂Œ������܂����D�H�������̌��̒��Ԃ̌ʂ��������D
���m�ʂ̕ł���̎���ɑ���n[�����ŕ\���ꂽ���̑召��r�ɂ��ā^18.6.24�n
�L�����Ƃ̊W�������ė~����
�����m��ҁn�F�A�����肪�Ƃ��D���w�Z�̋��ȏ��ł́u����̗L�����v�Ƃ����p�ꂪ�o�Ă���Ƃ͌���Ȃ��̂ŁC�u����ɍ������Ȃ��`�v�Ƃ����薼�Ő擪�̃T�u���j���[�ɂ܂Ƃ߂Ă��܂��D������ǂނƊW���킩��܂��D
���m�ʂ̕ł���̎���ɑ���n[��������iNo.�R�������^�j�ɂ��ā^18.6.10�n
���߂ė����ł��܂����I���肪�Ƃ��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~�ɓ��ڂ���l�p�`�ɂ��ā^18.6.09�n
PC�ŗ��p���Ă��܂����A����ɏo�錻�݈ʒu�́u�~�ɓ��ڂ���l�p�`�@�v��I��Ŋw�K�����PC�̃��j���[���D�ł́u�~�ɓ��ڂ���l�p�`�A�v���w�K�ς̐F�\���ɂȂ�܂��B
�����m��ҁn�F�A�����肪�Ƃ��D���j���[��ʂ̐����ԍ����t�ł����̂Œ������܂����D�ڂ��������ƁC���̋���
�~�ɓ��ڂ���l�p�`�̕�����ɍ�����̂ł����C������ڂ������Ă��邤���ɁC������̕������S�Ҍ����ɏ[�����Ă����̂ŁC���j���[��ʂőO�Ɏ����Ă������߁C����������ւ�����悤�ł��D
15���ɂȂ����ƁH
�����m��ҁn�F�A�����肪�Ƃ��D

�Ȃ�
1�����̃O���t�i�ؕЁj�̑�8��@4x-3y=12�̐ؕЂ����߂���ŁA������(0,-1)�ƂȂ��Ă��܂����A(0,-4)�ł͂Ȃ��ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D���̎���\�����邽�߂̃f�[�^�C���̃O���t��\�����邽�߂̃f�[�^�C�̎���\�����邽�߂̃f�[�^�C�̎���\�����邽�߂̃f�[�^�F�����S��ނ̓����i�V���N���j�����Ă��܂���ł����̂ŁC�������܂����D
���m�ʂ̕ł���̎���ɑ���n[�Q��C�������C���[�g�ɂ��ā^18.5.31�n
���[�g�Q�Ƃ��R�Ƃ����t�I���g�͂ǂ��ɂ���܂����B
�����m��ҁn�F�A�����肪�Ƃ��D�����⍪���Ȃǂ̐��w�L���́C�t�H���g�Ƃ��Ă͂���܂���D�v���O�������g���ď����ɂ́C(1)PDF (2)Google API (3)Google API (4)���̍�ғƎ��̃v���O���� �̂����ŁC�M�҂�(2)�܂���(4)���g���ď����Ă��܂��D
���̃y�[�W�ɊȒP�ȃ���������܂��D
����������Əڂ������肢���܂�
�����m��ҁn�F�A�����肪�Ƃ��D���Ԃ�3�����x�Łu�S����v�ɂȂ����̂ł��傤�D�����C�Ԉ���Ă�����C�ԈႢ�������}���\������܂����C�Ԉ��Ȃ������̂ŁC��������������o�Ȃ������̂�������܂���D
���m�ʂ̕ł���̎���ɑ���n[���̐��E���̐��ɂ��ā^18.5.31�n
�������o��悤�ɂ��Ăق���
�����m��ҁn�F�A�����肪�Ƃ��D���ꂾ���͂��Ȃ��ƌ��߂Ă��܂��D�l������ň�l�œǂ�ł���ꍇ�́C�e��������܂��C�w�Z�ł܂��͓d�Ԃ̒��œˑR�����o��̂͂悭�Ȃ��̂ŁC�����o��悤�ȋ��ނ́C�O�����āu���̋��ނ͉����o�܂��v�Ƃ����x�����\���m�点�Ă����K�v������܂�
���m�ʂ̕ł���̎���ɑ���n[�P���������̉������ɂ��ā^18.5.31�n
�Ј���50�������Ђ�����B���̓��A�j���Ј���25���Ə����Ј��̔�����
�@�@�@�d�Ԓʋ����Ă���A���v��18������B���̉�Ђ̒j���Ј��̐������߁A
�@�@�@�����̂ݓ�����B
�����m��ҁn�F���ނ̓��e�ƑS�R�W�̂Ȃ����Ƃ𑗐M���Ȃ��ł��������D�����̏h��͎����ł��܂��傤�D
���w2�N���̘A���������͂�����
�}���킩��₷��
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�P�����Ƒ������ɂ��ā^18.5.24�n
�ƂĂ��A������₷���Đ������₷�������ł��B���ƁA���ꂼ��͖����݂����Ȃ̂����Ă��ĉ��K���ł��ė������[�܂�܂���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������Q����Ƃ��̎��̒l�ɂ��ā^18.5.23�n
���������킩��₷���Ǝv���܂�
�����m��ҁn�F�A�����肪�Ƃ��D���������̂ɋC�t���Ȃ��̂́C�P��������������ɁC�������߂Ă����ꍇ�ł��D���ہC���Ȃ��̉�ʂ̐i�ݕ��ɂ͖��ɓ������`�Ղ�����܂���D
���m�ʂ̕ł���̎���ɑ���n[�H�����̔Z�x�ɂ��ā^18.5.23�n
�Z�x�͖ڂɌ����Ȃ����̂Ȃ̂ŁA�H��������
���t���o�Ă��������ŁA����[�B�Ǝv���ċ��ł������A���̉����������������₷���āA
����킩���Ă��܂���(^�[^)
���肪�Ƃ��������܂��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�S�����i�p�[�Z���g�j�ɂ��ā^18.5.22�n
�ǂ�����152�p�[�Z���g�Ȃ�Ă��蓾��̂��H
�Ȃ�
�����m��ҁn�F�A�����肪�Ƃ��D�p�[�Z���g�C�����Ȃǂ͊����̕\�����̂P�ŁC�Q�̗ʂ̈������Ƃ��đ����̊�����\�������̂ł��D
�`����ɂ��Ăa�̊�����\���ɂ́C�a���`�Ƃ��܂��D���Ƃ��C�挎�̎�����10���~�ō����̎�����25���~�̂Ƃ��C�挎�̎����ɑ��鍡���̎����̊����́C25��10=2.5�C������p�[�Z���g�ŏ�����250�p�[�Z���g�ɂȂ�܂��D�܂��C�����̑�����15���~��挎�̎����Ŋ����Ď����̐L�ї����v�Z���邱�Ƃɂ���C�����̐L�ї���150�p�[�Z���g�ɂȂ�܂��D
���̗�Ƃ��āC���140�l�̗�Ԃ�210�l�̏�q��������ꍇ�C��ԗ�150�p�[�Z���g�ł��傤�D
���̂悤�ɁC�������l����Ƃ��̕���ƕ��q�́C���ꂼ��̕���ł悭�g���ɉ����Č��߂���̂ŁC���q���K������̈ꕔ���ɂȂ��Ă���Ƃ͌���܂���D
���ۂɎg���邩�ǂ����m��܂��C���Ƃ��u�����Ԃ̎������v���u�����Ő��Y���ꂽ�����Ԃ̑䐔�������Ŕ��ꂽ�����Ԃ̑䐔�v�i�N������j�Œ�`����ƁC���q�ɗ���u�����Ő��Y���ꂽ�����Ԃ̑䐔�v�̒��ɂ͗A�o����鎩���Ԃ����������Ă���̂ŁC�����Ԃ̎�������150�p�[�Z���g�ȂǂƂȂ邱�Ƃ��l�����܂��D���̂悤�ɁC�����Ɏg������ƕ��q�́C��`�ɂ���ĕς����ł��D
���m�ʂ̕ł���̎���ɑ���n[��Βl�ɂ��ā^18.5.19�n
�w�Z�̎��Ƃł́A�����킩��Ȃ�������ł����ǁA����̂������ŁA������̃e�X�g�͑��v�����ł��I
�P����Ȃ�ł����A
��Βl��6�����̐��̐���S�Ă����Ȃ����B
��Βl��5�����̕��̐���S�Ă����Ȃ����B
�Ƃ��A
10�ȉ��̐��̐��ŁA��Βl��7���傫������S�Ă����Ȃ����B
�|10�ȉ��̐��̐��ŁA��Βl��7���傫������S�Ă����Ȃ����B
�ȂǂƂ������̈Ӗ���������܂���B
�悩������ڂ��Ă����Ə�����܂��B
���X�Ƃ��݂܂���ł����I
�����m��ҁn�F�A�����肪�Ƃ��D�ǂ̖����u�����v�Ƃ���������t���Ȃ��ƁC�����������ɂ����đS�ďq�ׂ邱�Ƃ͂ł��܂���D���ۂɓ�����ɂ́C�������̐}�������ΊȒP�ł��D
(1)�@��Βl��6�����̐��̐��������ׂČ����Ȃ���
x=1,2,3,4,5
(2)�@��Βl��5�����̕��̐��������ׂČ����Ȃ���
x=−1,−2,−3,−4
(3)�@10�ȉ��̐��̐��ŁA��Βl��7���傫�����������ׂČ����Ȃ���
x=8,9,10
(4)�@�|10�ȉ��̐��̐��ŁA��Βl��7���傫�����������ׂČ����Ȃ���
�|10�ȉ��̐��̐��Ƃ������̂͂Ȃ�
(�T)�̉�����ލ����W�߂鏊��20y��20x�ɂȂ��Ă��܂��B
���m�F���肢�������܂�
�����m��ҁn�F�A�����肪�Ƃ��D�������܂����D
���m�ʂ̕ł���̎���ɑ���n[�������ɒ������K�ɂ��ā^18.5.12�n
������������܂ŏo���Ē���������₷�������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������g�������ɂ��ā^18.5.12�n
�|�C���g���悭��������Ă��đ�ώQ�l�ɂȂ�܂����B���肪�Ƃ��������܂����I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����̎g�p�ɂ��ā^18.5.12�n
�ʔ����̂łǂ�ǂ���������Ȃ�܂����I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������̕\�����ɂ��ā^18.5.12�n
�Q�l�ɂȂ�܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[����ɂ��ā^18.5.11�n
���U�@�Q�D�\�̒��ŁA�����Q�̂Ƃ��A����-�P�ł͂Ȃ��ł��傤���H
�����m��ҁn�F�A�����肪�Ƃ��D�������܂����D
���m�ʂ̕ł���̎���ɑ���n[�����̎��ɂ��ā^18.5.11�n
���Q�ŁA�����́i�S�j���N���b�N���Ă�☓�ɂȂ��Ă��܂��܂��B�i�Q�j���N���b�N����Ɓ��ɂȂ�܂����B
�����m��ҁn�F�A�����肪�Ƃ��D�������܂����D
���m�ʂ̕ł���̎���ɑ���n[�����v�Z(�������) �ɂ��ā^18.5.8�n
���K���͌P���A�b�B�ł��B�ʔ��������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���ލ����܂Ƃ߂��ɂ��ā^18.5.7�n
���������J�ɐF��������Ă��ēǂ݂₷�����ƂĂ��킩��₷���ł��B
�e�X�g�O�ɎQ�l�ɂ����Ă��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Q���������̉������ɂ��ā^18.5.4�n
2�����-5��+2�̈��������������Ă�������
�����m��ҁn�F���̃y�[�W�̓��e�ƑS�R�W�̂Ȃ����ł��D���Z���Ȃ�C�����̏h��͎����ł��܂��傤�D
�������|����������
���Ȃ����čl���������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D�����ɓ��Ă͂߂��瓚���o��������C�����ł��Ȃ������ł��Ȃ��ƍl���邱�Ƃ͂悢���Ƃ��Ǝv���܂��D
���m�ʂ̕ł���̎���ɑ���n[���s���Ɛ����̔��ɂ��ā^18.4.30�n
�y���R�z
�@�}6������ BD//CE , a=5 , c=2 , z=3 �̂Ƃ��Cx �̒��������߂Ȃ��� �}5�̌��ł�
�����m��ҁn�F�A�����肪�Ƃ��D�g�єłŏc���ɂȂ��Ă����ʂ��CPC�ł�2�i�g�ɂ����Ƃ��ɁC�ԍ����Y�����悤�ł��D
���m�ʂ̕ł���̎���ɑ���n[�����̕ό`�ɂ��ā^18.4.28�n
�ƂĂ�������₷�������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Q��C�������C���[�g�ɂ��ā^18.4.28�n
��ϕ�����₷�������B�ǂ������肪�Ƃ��������܂����B���̂悤�ȕ����R�����Ă�������
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Q��C�������C���[�g�ɂ��ā^18.4.28�n
��ϕ�����₷���ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�_�Ώ̂Ȑ}�`�ɂ��ā^18.4.27�n
�Ƃ��Ă��悢�ł��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�O�����̒藝�ɂ��ā^18.4.24�n
��萔�𑝂₵���ق��������Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D��ʂ̍��̗��ɃT�u���j���[������܂��D���ꂪ�S���C�O�����̒藝�̖��ł��D
���m�ʂ̕ł���̎���ɑ���n[���̑̐ςƕ\�ʐ��ɂ��ā^18.4.22�n
��艉�K�̃v�����g������ė~�����ł��B
�Z�����Ǝv���܂�����낵�����肢���܂��I
�����m��ҁn�F�A�����肪�Ƃ��D���̃y�[�W�̐擪�ɁC����pPDF�łւ̃����N�������Ă���܂��D�i�����Ă���̂ɁC����Ă���ƌ�����̂́C�������Ȃ��̂��j�D����android�ɂ̓l�b�g���[�N�E�v�����^���C���X�g�[������Ă���̂ł����H
���m�ʂ̕ł���̎���ɑ���n[���ʐ}�`�̗p���ɂ��ā^18.4.22�n
�����킩��₷���ł��B
�ƂĂ�������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[��Βl�ɂ��ā^18.4.22�n
���̐���������₷���ł��I�I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���ލ��ɂ��ā^18.4.17�n
���A�o�J�߂��Ă悭����������c😢
�����������Ǝv���āA���������������ǁA����ς薳�����I�ł������ǂ�ʼn��ƂȂ��͕��������I�I�I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�P�����Ƒ������ɂ��ā^18.4.15�n
�������ł́Fx2+3xy−x+3 �� ������2�i�Q�����Ƃ����j
�@���Q�����Q����Ƃ��������͂Q���Ƃ���B�i�����Ȃ�Q�Ƃ��ō��j
���̏ꍇ�A����2��ƂR�����̂������A�����ʂŁu�ł����������v�ɂȂ�ƍl���Ă悢�̂ł��傤���B
�����m��ҁn�F�A�����肪�Ƃ��D���̒ʂ�ł��D
���m�ʂ̕ł���̎���ɑ���n[�P�����Ƒ������ɂ��ā^18.4.14�n
�P�����Ƒ������̐������ڂ����ȒP�ɏ����Ă����āA�ƂĂ����ɂȂ�܂����I
���������A�e�X�g������̂ł����A�����ŕ��������Ƃ�����悤�ɂ��Ă��������ł��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����̐����ɂ��ā^18.4.14�n
���̂Ƃ���ŁA�I��ł��������A�킩��₷���ĂƂĂ��ǂ������ł��I
�ł��A��肪�ȒP�߂����Ǝv���̂ł��������A������Ă������Ǝv���܂��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���ލ����܂Ƃ߂��ɂ��ā^18.4.12�n
�Ux2�{�T�{�Rx
�̏ꍇ�͑傫����������ׂ܂����H
���@�Ux2�{�Rx�{�T
��������Đ��w�̐搶���狳�����܂����B
�����m��ҁn�F�A�����肪�Ƃ��D����͂����Ȃ�ł����C���̃y�[�W�łȂ����̘b���o�Ă���̂��C�Ӗ��s���ł��D�~�ׂ��̏��ɐ������邱�Ƃ́C�P�O�̃y�[�W�ɏ����Ă���܂��D���̃y�[�W�ɂ́C���̘b�͏����Ă���܂���D
���m�ʂ̕ł���̎���ɑ���n[�S�����ɂ��ā^18.4.12�n
500�~�����������ɖ߂��Ƃǂ��Ȃ�H������
�����m��ҁn�F�A�����肪�Ƃ��D���w�Z�S�N�����炢�̂Ƃ��ɁC�����������ł��Ă��Ȃ��ƌ���ꂽ���Ƃ͂���܂��H���̎���́C���Ƃ��Đ��藧���Ă��܂���D500�~������500�~�����ŁC����Ȃ���Ί����ɂ͂Ȃ�܂���D
���m�ʂ̕ł���̎���ɑ���n[���Ώ̂Ɠ_�Ώ��ɂ��ā^18.4.12�n
�ʔ����B�N�̂Ȃ́A�Ȃ�Ȃ�����̒n�}
�����m��ҁn�F�A�����肪�Ƃ��D�N�̖��́B�Ƃ����A�j���̘b�����Ă���悤�ł����C��͒��ԓ������Œʂ���p��H
���m�ʂ̕ł���̎���ɑ���n[���������ɂ��ā^18.4.11�n
�킩��₷���Ă����ł��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�ςƘa���l������������ɂ��ā^18.4.11�n
�ƂĂ��킩��₷���A���₷���ł��I�I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�P�����Ƒ������ɂ��ā^18.4.10�n
�i��j
�P�U��x
���������Ă��鎮�ł́A�����Ƃ��Đ����Ă������ł����H
�����m��ҁn�F�A�����肪�Ƃ��D
��=3.14…�̂悤�ɓ���̐����X�Ə������ɂP�̋L���ŕ\�������̂́C�u�L���萔�v�ƌ����邱�Ƃ������Ǝv���܂����C���̗p��͒��w�Z�̐��w�̋��ȏ��ɂ͂Ȃ��悤�ł��D�������C����́u�����𐔂��镶���ł͂Ȃ��C�P�Ȃ�萔�v�Ƃ��Ĉ������Ƃ��d�v�ł��D
�y��z
(1)�@16��x → 1�����i��=3.14…�͉~�����j
(2)�@2.0g → �萔�ig=9.80665 m/s2�͏d�͒萔�j
(3)�@ → 2�����i
→ 2�����i =1.4142…�͂Q�悵����Q�ɂȂ�萔�j
=1.4142…�͂Q�悵����Q�ɂȂ�萔�j
�萔���͒P�����Ƒ������A�����Ƃ��ɂ���܂����H
�����m��ҁn�F�A�����肪�Ƃ��D�������܂܂Ȃ�����萔���Ƃ����̂ŁC���ʂ͒萔���͑������̒��̐�����������ł��Ă��鍀���l���܂��D�P�������萔����������C�萔�Ƃ��������������邱�Ƃ͑����Ǝv���܂����C�萔���ƌ����Ă��\��Ȃ��ł��傤�D

�ɂ����āC

��萔���Ƃ����܂����C���̒�`��

�̏ꍇ�ɂ��g���܂��D
3����1�~ 2�~ �|4����x���Ăǁ[���́H
�����m��ҁn�F�A�����肪�Ƃ��D������e�ƌ��Ă���y�[�W���Ⴂ�܂��D
�P�����������������D
�S�R�킩��܂���B
�����Ɓc�ڂ����̂��Ă��������B
�����m��ҁn�F�A�����肪�Ƃ��D������Ȃ��ꍇ�́C
�����ƑO�̕����猩�Ă��������D
��肪���邩��ƂĂ�������₷���A���ɂȂ�܂����B�}�`�����̂͂ƂĂ��ǂ��ł��ˁB
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Q���������̉������i�܂Ƃ߁j�ɂ��ā^18.4.7�n
���̌����̗�13�̖��I�����������5����3�}2��6���Ǝv���܂����c�c��������ł����Ă���̂Ȃ�}�C�i�X�����闝�R�������Ă�������
�����m��ҁn�F�A�����肪�Ƃ��D�����ɊԈႢ������܂����̂Œ������܂������C���Ȃ��̍l���Ƃ͂��傤�Njt�ł��D

������C���q��1���̕����͕��ɂȂ�܂��D
���͋�����}�`���A�w�Z�̉��̐Ȃł��A��l�����o���Ȃ������̂ŁA5����̉�����ƂĂ�������₷�������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���Ώ̂Ȑ}�`�ɂ��ā^18.4.3�n
�ƂĂ�������₷�������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�_�Ώ̂Ȑ}�`�ɂ��ā^18.4.2�n
�V��6�̎Z���ŏ��߂ɕ�����P���ł��B���s�l�ӌ`�͐��Ώ̂ł͂Ȃ��_�Ώ̂Ƃ������Ƃ��}�`���Ċm���߂���̂ŁA��ώQ�l�ɂȂ�܂����B�܂�������肪�m�̏h��ɂ��o�āA�ǂ��_�����܂����B���肪�Ƃ��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�H�����̔Z�x�ɂ��ā^18.4.1�n
�ŏ��́u��90(��)�ɐH��10(��)���n���Ă���H�����̔Z�x�́v�̖��Ɉ�a��������܂��B���ɐH�����n���Ă���A�ƂȂ��Ă���̂ł����琅�̒��ɐH�����n���Ă����Ԃ�90g���Ƃ������߂ɂȂ�܂��H�u��90(��)�ƐH��10(��)���n���Ă���H�����̔Z�x�́v�łȂ���Ή��߂��ς��Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D���k�łȂ��Љ�l�̕��ł��̂ŁC������Ȃ��ŁD�n�}�ɗn����n�����Ɨn�t�ɂȂ�Ƃ����������͂悢���C�n�}�ɗn�����n���Ă���i���ʂ��n�}�Ɖ��߂ł��邩��j�ƌ����Ă͂Ȃ�Ȃ��Əq�ׂĂ�����悤�ł����C�H�����n�������ʂ͐��Ƃ͌����܂���D
�n�}�ɗn����n�������Ƃ��C�n�}�ɗn�����n���Ă���ƌ����͉̂�����肪�Ȃ��ƍl�����܂��D
���m�ʂ̕ł���̎���ɑ���n[�������̍����ɂ��ā^18.3.31�n
�ƂĂ������Ǝv���܂�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[��������iNo.�R�������^�j�ɂ��ā^18.3.23�n
�C���X�g�����菮�X�킩��₷�������ł��B
�܂�����������\�̒�����I�Ԗ��Ȃ̂ł��炷��Ɖ����܂����B���肪�Ƃ��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���Ώ̂Ȑ}�`�ɂ��ā^18.3.22�n
�ȒP�ł����@�@
���ɂȂ�܂���
���肪�Ƃ��������܂���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�P���������ɂ��ā^18.3.22�n
�ƂĂ��f���炵���ł�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������̌v�Z�ɂ��ā^18.3.22�n
�ƂĂ��킩��₷�������B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Q��ƂR���ɂ��ā^18.3.22�n
�{���ɕ�����₷���ėǂ��ł��ˁI���z�ɂ܂��܂����������Ⴂ�܂��I�I
�V���������A�����o���ė~�����f�X�l�I�I
�����A������_������܂��Ė�蕶���킩��ɂ����Ƃ���ł��B
�Ȃ̂ł������A������P���ė~�����ł��I
����Ɋ��҂��Ă��܂�
�����m��ҁn�F�A�����肪�Ƃ��D�i���������܂Łj
���m�ʂ̕ł���̎���ɑ���n[�����̎g�p�ɂ��ā^18.3.22�n
�������̖������߂ĉ����܂����B������������Ď������ł��Ȃ��Ƃ��낪�킩�����̂ł悩�����ł��B
���肪�Ƃ��������܂�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�s�����̉������ɂ��ā^18.3.22�n
�킩��܂���I��������������₷�������ė~�����ł��I
�����m��ҁn�F�A�����肪�Ƃ��D����ے����ς���āC���݂͒�1�ŏK��Ȃ��Ǝv���܂�.���̋���ے������܂ł̑��ɒu���ꏊ���Ȃ��̂ł����ɂ����Ă���܂��D
���m�ʂ̕ł���̎���ɑ���n[�����̎g�p�ɂ��ā^18.3.22�n
������肾�Ǝv���܂�
������킩��₷���ď�����܂�
�����m��ҁn�F�A�����肪�Ƃ��D�i�����P�̊w�Z����ߑO��������2300���]��̃A�N�Z�X�������āC���z�������̂ł����C�Ή�������܂���̂ŁC��Ȃ��̂����f�ڂ��܂��D�j
���m�ʂ̕ł���̎���ɑ���n[�l���v�Z�̗D�揇���ɂ��ā^18.3.20�n
()���̌v�Z�͍ŗD�悳���킯�ł����A����ɂ����������̂͂ǂ��Ȃ��ł��傤���H
6 �� 2(1 �{ 2)
����A6 �� ( 2 �~ 3) ��1 �ɂȂ�̂��@6 �� 2 �~ 3 ���@�����珇�ԂɌv�Z���� 9 �ɂȂ�̂�
����1�ɂȂ�Ǝv���Ă����ł����c
�����m��ҁn�F�A�����肪�Ƃ��D���̖��ɂ��ẮC�P�����O�ɂ����Ă��܂����C�Ⴆ��
2×a�̂悤�ɁC�|���Z������O�̂��̂�
2a�̂悤�Ɋ|���Z���������ʁi�ρj�Ƃ��ĂP�̒l�ɂȂ������̂̂ǂ����\�����ɂ��āC�i�@�j������ƃg���b�L�[�Ȗ�肪����Əq�ׂĂ�����悤�ł���
�@�Ⴆ�C�����Ɛ����̊Ԃɉ��������Ȃ�
2 3�̂悤�ȋL����
2(3)�̂悤�ȋL���͎g���܂���D
�@

��

��\���܂���D�������C�����͂P�̕������Ƃ��Ĉ���

��

���v�Z�������ʂ�\���܂��D
�y�܂Ƃ߁z
�i�����ƕ���,�����ƕ����̊Ԃ́~���ȗ������猋�ʂ�\���j

�i�����ƍ����̊Ԃ́~���ȗ������猋�ʂ�\���j

�i�����ƕ����̊Ԃ́~�͏ȗ��ł��Ȃ��j
&chf=fffff3)
←�ʏ폑���Ȃ�������
�i�����Ɛ����̊Ԃ́~�͏ȗ��ł��Ȃ��j
&chf=fffff3)
←�ʏ폑���Ȃ�������
������������₷���Ă悩�����ł�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����̐����ɂ��ā^18.3.17�n
�����̏ꍇ���Ȃ��č���܂���
�����m��ҁn�F�A�����肪�Ƃ��D���̃y�[�W�̐擪�Ɂu���ݒn�v�Ə������T�u���j���[������C�����̃y�[�W����R����܂��D
���m�ʂ̕ł���̎���ɑ���n[2��̈��������ɂ��ā^18.3.16�n
36X���|4
�����m��ҁn�F���₪����Ȃ�C����炵�������܂��傤�D�Ȃ��C���Ă���y�[�W���Ⴂ�܂��D
�������̃y�[�W�ɏ����Ă���܂��D
��{�I�Ȃ��̂����łȂ��A����������̂��o��
�������́A�������̃��x����
����Ă����Ăق����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D���̃y�[�W�̐擪�Ɂu���ݒn�v�Ə������T�u���j���[������܂��D���Ȃ���������̂́C��ԍŏ��̂P�y�[�W�ł��̂ŁC���̎��̃y�[�W�ɐi��ł��������D
���m�ʂ̕ł���̎���ɑ���n[�S�����i�p�[�Z���g�j�ɂ��ā^18.3.13�n
�킩��₷��
���w���T�{��܂����Ăč��S�����K���Ń}�W�ł킩��₷��
�����������������Ƃ��Ă�������ق���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�s�����ɂ��ā^18.3.10�n
�s�����͒�1�͈̔͂ł������A��������Y��Ă��܂����B
�����m��ҁn�F�A�����肪�Ƃ��D����ے��̉����������āC�s�����̎�舵���͂��Ȃ�ς��܂����D���݂ł́C�s��������舵���Ă���̂����w1�N�������Ȃ̂ŁC�����ɉ��u�����Ă��܂����C����f���Ă��܂���D
�@���݂̋��ȏ��ł́C3>5��3<5�̂ǂ��炪����������I������̂悤�ɁC�萔�̑召��s�����ŕ\�����Ƃ����S�ł��D�s�����̒��ɖ��m�����܂܂�Ă�����C�u�s����x+3<5�������v�Ƃ�����Ȗ��́C�i�����w�Z����ɍl����Ɓm���w�Ƃ�������тł͂��̋�ʂ͂Ȃ��ł��傤�n�j���Z1�N�ŏ��o��̂悤�ł��D
���m�ʂ̕ł���̎���ɑ���n[1�����ɂ��ā^18.3.9�n
���|�����W�c����n�܂�������ڂ��Ăق����B
�����m��ҁn�F�A�����肪�Ƃ��D�ʏ�C���w�̋��ȏ��ł͂��̌����͈����܂���D���Z���Ȃ�
���Z�������̃y�[�W�����Ă��������D
��Ɠ����̖��P�O�A���q���W�߂���F�Troute3/3�ł́H
�����m��ҁn�F�A�����肪�Ƃ��D�Ō�̎��ɓ��̓~�X������܂����̂Œ������܂����D
���m�ʂ̕ł���̎���ɑ���n[�P�����Ƒ������ɂ��ā^18.3.9�n
�Ⴊ�����ĕ�����₷���ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Ώ̈ړ��ɂ��ā^18.3.7�n
���Ώ̈ړ��ł͂Ȃ��A�Ώ̈ړ����Ǝv���܂��B
�E�`�̊w�Z�̋��ȏ��ɂ́A�u���Ώ̈ړ��v�Ƃ������t���o�Ă��܂���B
�����m��ҁn�F�A�����肪�Ƃ��D����Ș_�_�Ŋ撣���ĉ��ɂȂ�̂��^��ł��D�����������w�Z�̋��ȏ��ɂ́C�ړ��Ƃ����p��͂Ȃ��i���3�Ёj�悤�ł��i�Q�l���ɂ͂���܂��j�D�Ώ̈ړ��Ƃ����p����Ȃ��̂ł��D���Z���܂߂����w�p��Ƃ��ẮC���s�ړ��C�Ώ̈ړ��C��]�ړ��������ĥ���_�Ώ̂͑Ώ̈ړ��ł͂Ȃ��ĉ�]�ړ��ť���Ƌ��������������₷���Ƃ͎v���܂��C���ȏ��ɏo�Ă��Ȃ�����u�������|�����������v�Ƃ����p��Ȃǂ��g���Ă͂����Ȃ��Ƃ��v���܂���D
���m�ʂ̕ł���̎���ɑ���n[�P�����Ƒ������ɂ��ā^18.3.5�n
�����قǑ���������͊ԈႢ�ł����B
���̂悤�ɒ����������܂��B�i�u�������v���u�u�ǂ���ł��Ȃ��v�ɕύX�E�j
���3�̒P�����ł��邩�������ł��邩��₤����5�ԖځA2/���̓������u�ǂ���ł��Ȃ��v�ƂȂ��Ă��܂��B
����͊ԈႢ�ŁA�������͒P�����um�v�ł͂���܂��H
�����m��ҁn�F�A�����肪�Ƃ��D���̃y�[�W�̐擪�����ʼnE�������Ă��������Dx������ɂ��鎮�́C�P�����ł��������ł��Ȃ��C�������ł��D�i���w2�N�̗p��Ƃ��Ă͏K���܂��C���w1�N�̔����̂Ƃ��Ɏ��Ƃ��Ă͏K���Ă��܂��D�j
���m�ʂ̕ł���̎���ɑ���n[�_�Ώ̂Ȑ}�`�ɂ��ā^18.3.5�n
�ƂĂ�������₷�������ł��I���̍l���ł͂����_����ꂻ���ł��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[2���������̉��ɂ��ā^18.3.5�n
===��2���������̉���===2�ځ�1�ڂ̕�����x+a=X�Ƃ���
�Ə����Ă���܂����Ax+k=X
���Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�����ł��D�������܂����D
���m�ʂ̕ł���̎���ɑ���n[�����v�Z�i�j�ɂ��ā^18.3.4�n
���ʂɎg���₷�������ł�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�A���������̍����ɂ��ā^18.3.4�n
��������������܂���B����A�������������Ƃ킩��₷���A�f�����Ă��炦��Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D����Ή���͏o�܂��D���Ȃ���Ή���͏o�܂���D���Ȃ��̊��z�́C�P��������Ă��Ȃ��Ƃ������Ƃ������Ă��܂��D���������āCPDF�ŏ����ꂽ���W�̂悤�ɁC���Ɠ������邾���̂��̂��ƍl���Ă��܂��H�����Ǝv�����̂��N���b�N����̂ł��D
���m�ʂ̕ł���̎���ɑ���n[���������ɂ��ā^18.3.2�n
����́u�ڂ������]���ɂ���Ƃ��āv�u�����ɂ���Ă�v���ƂĂ��킩��₷���āA�L���ɂ��c���Ă悢�Ǝv���܂����B�`������z���g�ɏI�����c�Ȑ��l���(���)
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�������������ƂȂ邎�̒l�ɂ��ā^18.3.2�n
������₷���A��肪���������ėǂ�����
�����m��ҁn�F�A�����肪�Ƃ��D
���H�m�H�^18.3.1�n
�u�H�����̔Z�x�v�̑���
��/�m����/�l�i���C�m�C���A�l��0�j�̂Ƃ��A��/�m���i��+���j/�i�m+�l�j����/�l�����B
���u�`���l�i��+���j�|���i�l+�m�j�ƒu���Ƃ`���l���|�m�����l�m�i��/�l�|��/�m�j��0����Ă�/�m���i��+���j/�i�m+�l�j����/�l�v�i������ƕЕ��͂�����Ă܂����A����Ȋ����ɂȂ�܂��ˁj
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�_�Ώ̂Ȑ}�`�ɂ��ā^18.3.1�n
��������������₷���I
�����m��ҁn�F�A�����肪�Ƃ��D���ꂪ�ڈ�t����
���m�ʂ̕ł���̎���ɑ���n[�H�����̔Z�x�ɂ��ā^18.3.1�n
���̔Z�x�̖��ł́A����ʔ������ۂ�����܂����B���̖��̓������A�Z�x�̊T�O���g���ƁA���w���ł������I�ɔ[���ł��邱�Ƃ�����̂ł��B�^�N�C�Y�{�Ō������u��̕����i�ѕ����͏����j�̕��q�ǂ����A����ǂ����������ďo���������̑傫���́A�K���ŏ��̓�̕����̒��ԂɂȂ邱�Ƃ�����i�ؖ��j���Ȃ����B�v�̓����́u�Z�x�̔Z���̂Ɣ����̂�������A�ł����n�t�̔Z�x��
������O�̓�̗n�t�̒��ԂɂȂ�i�����̐�������v���l���₷���j�v�ŁA�������̒ʂ�ƂȂ�܂��ˁB�h�ؖ�����h�ƌ�����Ɠr�f���܂���---�B�Z���ł͂��̂悤�Ɏ��ۂ̐�����̎��ۂɑ������l���ŁA�n������[���ł����肷����̂��ȊO�ɑ�������A�N�C�Y���Ȃǂ͂��������܂����p�������̂��ʔ������ɂȂ�܂��ˁB
�����m��ҁn�F�A�����肪�Ƃ��D
&chf=fffff3)
�̂Ƃ�

���ؖ�������́C���Z1�N�̔��`�������ӂ肩�ȁD
�q���g�ł͂Ȃ������ɂȂ��Ă���
�����m��ҁn�F�A�����肪�Ƃ��D�{�^���̃��x��������ɂ��܂����D
���m�ʂ̕ł���̎���ɑ���n[�������ɒ������K�ɂ��ā^18.2.28�n
�����͕���������ł����ǂ��w5�A49�x�������ꍇ�͂ǂ��Ȃ�̂ł����H�����͂ǂ��Ȃ邩�킩��Ȃ��āc�c�c
���݂܂���(�L�G�ցG`)
�����m��ҁn�F�A�����肪�Ƃ��D���̃y�[�W�̍����ł͏ォ��4�ԖځC�E���ł͏ォ��5�ԖڂɗႪ�����Ă���܂��D
 �ɂȂ�܂��D
�ɂȂ�܂��D
��������Ă����ɂ͉��������Ă���̂��C�����ł��܂���ł����D�p�ꕶ������X�|�[�c�V���Ȃǂł́C�����_�𒆓_�ŏ����āC
5•49�Ə������Ƃ�����C�p��ȊO�̕������ł́C�����_���J���}�ŏ����C3�����Ƃ̈ʎ����J���}��
1.234.678,49�Ə����悤�ł����C���{�̎��Ƃł�3�����Ƃ̈ʎ��̓J���}�ŁC�����_�̓s���I�h��
1,234,678.49�ŏ������@�����Ȃ��ł��傤�D5�A49�����͐�ɂȂ��g�������Ǝv���܂��D�iiPad�̊����ϊ��V�X�e���Ɋ���Ă��Ȃ��������������j
�����Ȃ��ꍇ�͂ǂ�����悢�̂�
�����m��ҁn�F�A�����肪�Ƃ��D��ӂ̒������P�ŁC�������P�̂悤�ȏꍇ�̂��Ƃ������Ă�����̂Ȃ�C����͑��v�C���ёO�ł��D�����⏬���œ�����̂ł��D�i�����̐��w�ł͕����̕����悭�g���܂��j�D

�Ȃ�
������킩��₷���ĂƂĂ��悩�����ł��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�_�Ώ̂Ȑ}�`�ɂ��ā^18.2.21�n
���A�u���ʐ}�`����{�̒����Ŗʐς������ɂ́A�ǂ������������悢���v�������Ă��܂��B�_�Ώ̐}�`�̂Ƃ��̂݁A�����̒����͕K�������_��ʂ�A�܂����̋t�����藧�A���Ȃ킿�A�u���̏d�S�_��ʂ钼���������A�ʐς͕K���������v���Ƃ��A�����I�ɕ�����܂����B�O�p�`�̏d�S�ł͂����͂Ȃ�܂���B�i�悭���Ⴂ����̂ł����j����͎O�p�`���_�Ώ̐}�`�ł͂Ȃ�����ł��B���̎������p����ƁA�����w���p�̖ʔ����}�`��肪���낢��ł��܂��B�Ⴆ�u��̒����`�̂��ꂼ��̈�ӂ��҂�����d�Ȃ�����`�i�ǂ̓��p��1�A�܂���3���p�ł��鑽�p�`�j�̖ʐς���{�̒����œ�����ɂ́A�ǂ̂悤�Ȓ����������悢���v�Ȃǂł��B
 �����m��ҁn�F
�����m��ҁn�F�A�����肪�Ƃ��D�����`�̑����Z�̏ꍇ�́C�H�Z�Ƃ����������N�O��TV�Ŏ������Ă���ꂽ�悤�ł��D�����₷���̂�2�{�����ˁD
����ɁC�����`�̈����Z�ł��s�������Ȋ����ł��D���}�̂悤�ɁC���`���R�̏�ɔ��`���R���͂�t���Ă���D�n���Ă��邤���ɉ��H�����̂ŁC���̉��ɂ͍��͂Ȃ��D���̃`���R���C�i�C�t�łP�����ɐ��āC2�l�̎q���ɔ������������ʐςɂȂ�悤�ɕ��������D�ǂ̂悤�ɐ�悢���D�Ȃǁi�������̃m���ł��悢�j
���̂Ƃ�����Ȃ��g���Ă܂��B
�������������܂��A���肪�Ƃ��������܂�😊
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�O�����̒藝�̉��p�ɂ��ā^18.2.16�n
�ƂĂ��Q�l�ɂȂ�܂���
�ǂ������肪�Ƃ�������������
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���Ώ̂Ȑ}�`�ɂ��ā^18.2.12�n
�}�`�������̂ŁA������₷���B
�������A��]���x�����������̂ŁA���x���ߋ@�\�Ȃǂ�����ƁA���ǂ����ނɂȂ�Ǝv���B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�ӎO�p�`�̊p�ɂ��ā^18.2.12�n
��ABC��AB��AC�̓ӎO�p�`�ł��BAD��AE�A�pDAE��43�x�A�pDBF��25�x�̂Ƃ��A�pBFC�̑傫�������߂Ȃ����B
�������������B
�����m��ҁn�F�A�����肪�Ƃ��D�w�Z��w�K�m�̏h��̌`�����Ă��鎿��ɂ͓����܂��C����ɁC���̖��ɂ͖��̎ʂ��ԈႢ������܂��D
���m�ʂ̕ł���̎���ɑ���n[�l���v�Z�̗D�揇���ɂ��ā^18.2.11�n
6��3�i1�{2�j�͂ǂ���������ł����H
�����m��ҁn�F�A�����肪�Ƃ��D�������̒��͗D��I�Ɍv�Z���܂����C��������ƂU��3(3)�ƂȂ�܂����C���ʂ��������������͂��܂���D3�~3�Ə�������33�Ə����C�S���ʂ̐�����\���Ă��܂��D������C����͖�肪�Ԉ���Ă���̂ł��D
���m�ʂ̕ł���̎���ɑ���n[�O�����̒藝�̉��p�ɂ��ā^18.2.9�n
������舵���ė~�����ł�
�����m��ҁn�F�A�����肪�Ƃ��D��������悢�ˁC�����ł�
��?�m���n[18.2.8�n
���͎��I�����Z�̗\�K�����Ă��܂��B���̎��ɏo�Ă���
�g6a^2+4ab-2b^2-10a+6b-4�h
�̂����������ĉ������B�o����A�������낵�����肢���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�܂�2�ł�����܂��傤�D���Ƃ�
���̃y�[�W�����Ă��������D
�_�Ώ́A���Ώ̂̈Ⴂ���悭�����ł��܂���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���Ώ̂Ȑ}�`�ɂ��ā^18.2.3�n
�ƂĂ������Ǝv������������킩��₷�������Ǝv��🌈☺
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Q��C�������C���[�g�ɂ��ā^18.2.1�n
�i2��3�j�Q�� ���v�Z�̎d�������ĉ������I
�����m��ҁn�F�A�����肪�Ƃ��D�h��̖�肩������Ȃ��̂ŁC�v�Z�̎d���������܂��D���͎����ōl���Ă��������D
�w���@���ɂ��C
(ab)n=anbn���P�����悵�����̂̐ςɂȂ�
������
�m��P�n
^2=3^2(\sqrt{2})^2=9\times 2=18&chf=bg,s,fff9f9)
�m��Q�n
^2=5^2(\sqrt{3})^2=25\times 3=75&chf=bg,s,fff9f9)
�m��R�n
^2=2^2(\sqrt{5})^2=4\times 5=20&chf=bg,s,fff9f9)
�̂悤�Ɍv�Z���܂��D�����^�����Ȃ���C
^2&chf=bg,s,fff9f9)
���l�����������D
���������ʼn����āA������Ȃ����̓q���g���o�Ă����Ǝv���B
�ƂĂ��g���₷���B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���Ώ̂Ȑ}�`�ɂ��ā^18.1.29�n
���������₷���Ă킩��₷���ł��I�I
�����������ƁA�����Ɂ��~���o��̂ŗǂ��ł��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�O�����̒藝�ɂ��ā^18.1.29�n
�����������Ǝv��
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�A���������̕��͑��ɂ��ā^18.1.28�n
�����̉������Ȃ̂��ԈႢ�Ȃ̂����Ԃŕ\������Ă�������ɂ����Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D���̊��z�͈ꌩ���炩�̎������w�E���Ă���悤�Ɍ����܂����C���͂��Ȃ����S��Ԉ�����Ƃ������Ƃ�������̂ł��D1��ł������ɂȂ����l�͂��̊��z�͌����܂���D�����Ƃ͂����茾���C���Ȃ��������y�[�W�͌��݂̂��Ȃ��̊w�͂ƍ��v���Ă��܂���D���[�̃T�u���j���[�ɂ�������@�����@���ɂ��ׂ��ł��D���͑�̑��̃y�[�W�𐔕b���Ă��܂����C�قƂ�ǐg�ɒ��Ă��܂���D
���m�ʂ̕ł���̎���ɑ���n[�H�����̔Z�x�ɂ��ā^18.1.28�n
����ł��B
�����m��ҁn�F�A�����肪�Ƃ��D���Ȃ����g�̏������Ă��܂���̂ŁC�����悤������܂���D��莩�̂͏��w�������̂��̂ł����C���Ȃ������w���Ȃ̂����w���Ȃ̂����킩��܂���D����google�Ō���������o�Ă����Ƃ��������ł͉����Ԃ��錾�t���Ȃ��ł��D
���m�ʂ̕ł���̎���ɑ���n[�O�p,���p�`�ɂ��ā^18.1.26�n
�ƂĂ��ǂ����ł����I
�����m��ҁn�F�A�����肪�Ƃ��D
�� ?�m N����^18.1.25�n
���̂��������₳���Ē�����N�ł��B���肪�Ƃ��������܂��B
���̎���̂������ō�҂��V���Ȕ��������Ă��������ƂĂ������������܂��B���ꂩ����g�킹�Ă��������܂��B���肪�Ƃ��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�ԈႢ�T���ɂ��ā^18.1.25�n
N�ł��B���P����Ă܂����B���肪�Ƃ��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�O�����̒藝�ɂ��ā^18.1.24�n
�ʂ̃p�^�[���̂��������
�����m��ҁn�F�A�����肪�Ƃ��D�y�[�W�̐擪�ɃT�u���j���[�������āC�ގ���肪����y�[�W��I�ׂ�悤�ɂȂ��Ă��܂��D
�� ?�m N����^18.1.23�n
�����g�킹�Ă����������肪�Ƃ��������܂��B
http://www.geisya.or.jp/ ~mwm48961/math/ mobile/mobile_index3.htm�̓��̗��̊ԈႢ�T���̃{�^����������http://www.geisya.or.jp/ ~mwm48961/math/mobile/ m3para03_m.htm�ɍs���͂��Ȃ̂ɁAhttp://www.geisya.or.jp/ ~mwm48961/math/mobile/ m3para02_m.htm�ɍs���Ă��܂��܂��B
�@�Ȃ��ł����H
�A���̌��ۂ́A����iPad�����ɋN�����Ă��܂����H
���Љ��肢���܂��B�����āA���Ȃ̂ł���A���P���Ă������������ł��B�X�������肢���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�ǂ̋@��ł��������Ǝv���܂��D�����N��̃y�[�W�����Ԉ���Ă���\��������܂��̂ŁC���ׂĂ݂܂��D
���łɁC���Ȃ��̎��₩��C���ꂵ�����Ƃ�������܂����DiPad������ې����@�A��������I- - �@��ˑ��������g���Ɠǂ߂Ȃ��ꍇ������̂ŁC�ې������ł��邾�������Ă��܂������C�A�b�v���n�ł��\�������̂�������C�����Ȃ��g����̂ł��ꂵ���D
���m�ʂ̕ł���̎���ɑ���n[�~�ɓ��ڂ���l�p�`�ɂ��ā^18.1.23�n
�w���v�͏�������
�����m��ҁn�F�A�����肪�Ƃ��D������Ȃ��l������̂ŁC�w���v�͕K�v�ł����C��蒼���{�^�����N���b�N�����Ƃ��ɁC����������Ăق����Ƃ����v�]�ł�����C���̂悤�ɉ��P���܂����D
���m�ʂ̕ł���̎���ɑ���n[�ԈႢ�T���ɂ��ā^18.1.23�n
���肪�Ƃ��������܂����B
�����Ɩ�肪����Ƃ����Ǝv���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�ԈႢ���Ă͌��\����Ǝv���܂����C���̃O���t�̎�ނ͉��ʂ肩�����Ȃ��C�v�����̂������ɏ����Ă��邭�炢�������Ƃ������Ƃł��D
���m�ʂ̕ł���̎���ɑ���n[���Ώ̂Ȑ}�`�ɂ��ā^18.1.23�n
�}�`�������̂������ėǂ�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Ϗ��ƈ����Z�ɂ��ā^18.1.22�n
�������낢
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�ڌ��藝�ɂ��ā^18.1.22�n
�������ł����B����ł������܂��B�ڌ��藝��������̂ɖ𗧂��܂����B���肪�Ƃ��������܂��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�W�J�����ɂ��ā^18.1.22�n
�u���������́v���u�������̂��v�ɂȂ��Ă���̂ŏC�����Ē��������ł��B
�����m��ҁn�F�A�����肪�Ƃ��D�����Ƃ��ƁC���b�̂悤�Ȍ�ϊ��Ő\����Ȃ��D�������܂����D
���m�ʂ̕ł���̎���ɑ���n[�ω��̊����ɂ��ā^18.1.22�n
�ǂ��Ǝv���܂�
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���������͂����ɂ��ā^18.1.19�n
2���A���������͂��܂�킩��Ȃ������̂ł��̂悤�ȃT�C�g������Ă���ĂƂ��Ă��������ł��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�����v�Z�i���̒l�j�̓������ �ɂ��ā^18.1.19�n
�i4�j�̉���́E�E�E�i�Q�j�̂Ƃ����x^3�̌W�����Ⴄ��Ȃ��ł����H
�����m��ҁn�F�A�����肪�Ƃ��D���̌W���Ɏʂ��ԈႢ������܂����̂Œ������܂����D
���m�ʂ̕ł���̎���ɑ���n[���l���E�X�̒藝,�`�F�o�̒藝�ɂ��ā^18.1.19�n
���3��a��b�������፬���c�����킩��܂���
�����m��ҁn�F�A�����肪�Ƃ��D���3�Ƃ������̂͂���܂���D
���m�ʂ̕ł���̎���ɑ���n[�Q�_��ʂ钼���̕������ɂ��ā^18.1.18�n
�ƂĂ�������₷�������ł悩�����ł��B������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Q�����̃O���t�ƒ����Ƃłł���}�`�̖ʐ��ɂ��ā^18.1.14�n
2�����̃O���t�̖ʐς̋��ߕ����킩��܂����B�w���v�̐������悭�킩��܂����B�L��������܂��B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�~���p�̒藝�ɂ��ā^18.1.13�n
hint�͕⏕����}�ɏo���Ηǂ�����
�����m��ҁn�F�A�����肪�Ƃ��D���������Ă���ƁC���̒��ɂ͌���I�F�����D�ʂ̐l�ƁC��I�}�`�I�F�����D�ʂȐl������炵���Ƃ������Ƃ�������̂ł��D�ǂ��炩�ƌ����C���Ȃ��͕M�҂Ɠ��l�ɔ�I�}�`�I�F�������ӂȕ��̂悤�ł����C���̎v�l�p�^�[���ɍ��v����l�͏����h�݂����ł��D������C���l����ΏۂƂ���v�������ނł́C��I�ȈÎ������ł͖����݂����ł��D
���m�ʂ̕ł���̎���ɑ���n[�Ώ̈ړ��ɂ��ā^18.1.12�n
�킩��₷��
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Q�����̃O���t�ƒ����ɂ��ā^18.1.8�n
����ς������(�� ˃̶͈̀��˂̶͈́)੭ꠥ⁾⁾
�������(�E�E?)
�ǂ�������c
���������� http://www.geisya.or.jp/ ~mwm48961/math/mobile/ m3para11_m.htm
�̊��z�̑��M�{�^�����Ȃ��ł���낵�����肢���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�㔼�F��x���M����ƁC�������o�߂��Ȃ��Ƒ��M�{�^���͏o�܂���D
�O���F�Q�����ƒ����̖��́u�����̎��v�u�Q�����v�u�A���������̉������v�̑S�����ł��Ȃ��Ɖ����Ȃ��C����u�����́v���������̂ŁC�������P���m���ɂł���悤�ɂ��邵���Ȃ��ł��傤�D���̃y�[�W������Ă���Ƃ������Ƃ͒��w�R�N���ŁC�����̒��O�Ƃ����ꍇ�ł��u�}���Ή��v�̕����悢�ꍇ������܂����C�S�R�_���ȏꍇ�́C���̃y�[�W�ɂ���u����v��^�����Ă悭�������������̂��P�̕��@�ł��D���S��������Ȃ��Ƃ��́C�^��������̂ł��D
���m�ʂ̕ł���̎���ɑ���n[�ω��̊����ƃO���t�ɂ��ā^18.1.8�n
�ȒP�ȉ��@�C�C�ld(^_^o)
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�f���������̉��p�ɂ��ā^18.1.7�n
���肪�Ƃ��������܂����B
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�O�����̒藝�ɂ��ā^18.1.7�n
������₷���Ă���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�O�����̒藝�ɂ��ā^18.1.6�n
�����`�Ɛ��O�p�`�����̒��ɓ���ė~���������B
�����m��ҁn�F�A�����肪�Ƃ��D���̃y�[�W�̏�[�ɖڎ�������̂ŁC�~�������̂��o�Ă���y�[�W��T���Ă�������
���H�m �V�L�����N����n[18.1.4�n
���b�`�����������������������������������������������������������B
���肪�Ƃ��������܂����B����̃e�X�g�Ɏg�������ł��B�����킩��₷���ď������܂����B
���Ȃ݂� 4x�~23y=280 ���ĂȂ�ł���?
�������肢���܂��B
�����m��ҁn�F�A�����肪�Ƃ��D�����Ăق����̂����͂����肳���Ȃ���C���Ƃ��Đ��藧���Ă��܂���D���̎������藧����x, y�̑g�͖�������܂��D
���m�ʂ̕ł���̎���ɑ���n[�������������ƂȂ邎�̒l�ɂ��ā^18.1.4�n
���P�_�͓��ɂȂ��Ǝv���܂��B
�����Č����A����n�̒l�����߂���ŁA
�ŏ��̂����������߂�Əo�����̂������ł�
�`�������ƂȂ�悤�Ȏ��R��n�̒l��S�ċ��߂�
�Ƃ����������o���ė~�����ł�
��ς��Ǝv���܂����ƂĂ����ɂȂ�܂��B
�撣���Ă��������B
�����m��ҁn�F�A�����肪�Ƃ��D����������ꍇ�ɁC���������Ƃ͂ł��Ȃ��ł��傤�i���w���ł͓������Ȃ��ꍇ������j�D�܂��C����������ꍇ�ɁC�ꕔ�����C�ꕔ�s�����̏ꍇ�̍̓_���ʂ̕\��������ł��傤�D
���m�ʂ̕ł���̎���ɑ���n[�������������ƂȂ邎�̒l�ɂ��ā^18.1.4�n
���肪�Ƃ��������܂���
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[���z���ɂ��ā^18.1.4�n
"�A�����肪�Ƃ�"
�����ōς܂��̂�߂���H
�Ȃ����z���ۂ���B
�܂��A�ق��ɈĂ�����킯�ł�Ȃ����c
�܂��A�Z������ł��傤���ǁB
�����g�킵�Ă�����Ă���̂ɂ���Ȏ������̂͗ǂ��Ȃ��Ǝv�����ǁc�[�q�\�R���K���o�b�e�z�V�C�i�@�`�g�I���C�}�X�B
�����m��ҁn�F�A�����肪�Ƃ��D����łȂ��ꍇ�ɁC���������Ƃ͂ł��Ȃ��ł��傤�D
���m�ʂ̕ł���̎���ɑ���n[�O�����̒藝�ɂ��ā^18.1.4�n
��ӂ̒�����1:1.5�̏ꍇ�̌v�Z���́H
�����m��ҁn�F�A�����肪�Ƃ��D���₪�s���m�E�s���m�ł��D��ӂ̒�����1:1.5�Ƃ������Ƃ͂���܂���D
���m�ʂ̕ł���̎���ɑ���n[�H�����̔Z�x�ɂ��ā^18.1.2�n
�ƂĂ��ǂ�����
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�O�p�ɂ��ā^18.1.2�n
�����Ă��Ƃ���ԈႦ���Ƃ��Ȃǂɏo��G���ʔ����A��������������₷���{���ɕ��ɂȂ�܂��I
�@�����͊O�p�ł͂Ȃ��B�Ȃǂ́A���ȏ��ɂ͍ڂ��Ă��Ȃ��悤�Ȃ��Ƃ�A�w���v�̂킩��₷�����A�������Ǝv���܂����I
�@�{���ɂ��肪�Ƃ��������܂��I
�����m��ҁn�F�A�����肪�Ƃ��D
���m�ʂ̕ł���̎���ɑ���n[�Β��p,���ʊp,���p�ɂ��ā^18.1.2�n
���т��オ��܂����I
�킩��₷���āA�ƂĂ��֗��ł��I
���ꂩ������̃T�C�g�ł����������Ǝv���܂��I
�����m��ҁn�F�A�����肪�Ƃ��D
��==���j���[�ɖ߂��@�@�ȑO�̊��z��==��

 ���m�ʂ̕ł���̎���ɑ���n[���s���Ɛ����̔��ɂ��ā^20.12.24
���m�ʂ̕ł���̎���ɑ���n[���s���Ɛ����̔��ɂ��ā^20.12.24
 (A)�̂悤�ɑΏ̂̎������߂�ꍇ�C���̉E�ɂ͉����Ȃ��D���̍��������ɉf�����悤�ɉE�Ɉڂ��ƁC���E�S�̂łP�̐��Ώ̂Ȑ}�`�ɂȂ�D
(A)�̂悤�ɑΏ̂̎������߂�ꍇ�C���̉E�ɂ͉����Ȃ��D���̍��������ɉf�����悤�ɉE�Ɉڂ��ƁC���E�S�̂łP�̐��Ώ̂Ȑ}�`�ɂȂ�D (1) �ӂ�6cm�ŗ���p��30���̏ꍇ�F
(1) �ӂ�6cm�ŗ���p��30���̏ꍇ�F
 �����m��ҁn�F�A�����肪�Ƃ��D�����`�̑����Z�̏ꍇ�́C�H�Z�Ƃ����������N�O��TV�Ŏ������Ă���ꂽ�悤�ł��D�����₷���̂�2�{�����ˁD
�����m��ҁn�F�A�����肪�Ƃ��D�����`�̑����Z�̏ꍇ�́C�H�Z�Ƃ����������N�O��TV�Ŏ������Ă���ꂽ�悤�ł��D�����₷���̂�2�{�����ˁD