|
現在地と前後の項目 *** 二次関数の基本 *** /間違い探し/対応表の完成/関数の用語/係数の決定/ *** 放物線のグラフ *** /点→関数（解説）/点→関数（問題）/関数→点1/関数→点2/関数形の決定（解説）/関数形の決定（問題1）/関数形の決定（問題1）/ *** 変化の割合 *** /変化の割合1/変化の割合2/変化の割合3/変化の割合とグラフ/変化の割合(入試問題)/変域(1)/変域(2)/ *** 面積 *** /放物線と直線→面積1/放物線と直線→面積2/放物線と直線→面積3/2次関数のグラフと直線/放物線と三角形の面積1/放物線と三角形の面積2/ *** まとめ *** /放物線と直線/
【要点】
yがxの関数であるとき，xの値がx1からx2に変化したとき，yの値がy1からy2に変化する場合，
yの増加量
xの増加量
すなわちを変化の割合といいます．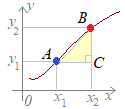 
1.xの増加量は，xの最後の値x2からxの最初の値x1を引いたもの，すなわち （xの増加量）＝x2−x1 によって定義されます． この引き方の順序を間違わないように気を付けましょう．
【例】
2.yの増加量は，yの最後の値y2からyの最初の値y1を引いたもの，すなわち(1) xの値が1から3に変化するとき， （xの増加量）＝3−1=2 (2) xの値が−1から5に変化するとき， （xの増加量）＝5−(−1)=6 ※xの増加量は，xの最後の値x2からxの最初の値x1を引いたもの，によって定義されますので，理屈の上ではx2<x1の場合でも，（xの増加量）として負の数を考えればよいのですが，中学生向けの教材では，ほとんどが（xの増加量）は正の数になっています． ※これに対して，次に述べる（yの増加量）は正の数になる場合も，負の数になる場合もあります． （yの増加量）＝y2−y1 によって定義されます．
【例】
(1) yの値が2から6に変化するとき， （yの増加量）＝6−2=4 (2) yの値が2から−1に変化するとき， （yの増加量）＝(−1)−2=−3 ※この(2)の例のように，最後の値が最初の値よりも小さいときは，実際にはyの値は減少していますが，このような場合でも（yの増加量）といい，負の値で表します． ※文章題をやっている場合のように国語的に考える場合は，(2)の例では「yの減少量が3」と言っても同じ内容を表しますが，数学ではこのような場合でも， （yの増加量）＝−3の形で減少する場合を符号で示すことが多い． 右上に続く↑
|
yの増加量
xの増加量
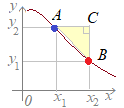
で定義されているので，分子にyの増加量を，分母にxの増加量をもって来なければなりません．図１においては，分母は横の長さAC，分子は縦の長さBC，すなわち
縦
横
なので，「変化の割合」は「線分ABの傾き」を表しています．図２においても同様ですが，図２においては，yの増加量として，BCの長さに負の符号を付けて考えています．この場合，「変化の割合」が負の値になることは「線分ABの傾き」が負の値になること，すなわち右下がりになることに対応しています．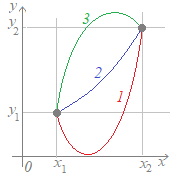 
によって，すなわち最初の点の座標(x1, y1)と最後の点の座標(x2, y2)だけで決まるので，途中の経路がどうなっているのかに関係なく定まります． 右図３において，赤で示した経路１であっても，青で示した経路2であっても，緑で示した経路3であっても，変化の割合はすべて等しくなります．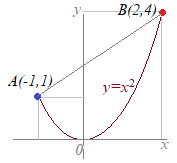 
になり，途中で減ってから増えているという経路は考慮しません．この変化の割合は点A(−1, 1)と点B(2, 4)を結んだ線分ABの変化の割合と全く同じものです．
【例題１】
（解答）関数 （東京都2015年入試問題）
x=6のとき，y=12
x=9のとき，y=27 変化の割合は
４種類の数字が登場するので，落ち着いて，「最後のx」「最初のx」「最後のy」「最初のy」と確認しながら書き込むようにします．
|
|
※以下に引用する高校入試問題で，元の問題は記述式の問題ですが，ｗｅｂ画面上で入力問題にすると操作性が悪いので，選択問題に書き換えています．
【問題１】 （画面上で解答するには，選択肢の中から正しいものを１つクリック）
(1)
関数y=−3x2について，xの値が1から3まで増加するときの変化の割合を求めなさい。 （愛知県Ａ 2017年入試問題）
|
(2)
関数y=−x2について，xの値が1から4まで増加するときの変化の割合を求めなさい。 （宮崎県2017年入試問題）
|
|
(3)
関数y=2x2で，xの値が0から2まで増加するときの，変化の割合は4である。xの値が−2から0まで増加するときの，変化の割合を求めなさい。 （岐阜県2000年入試問題）
|
(4)
関数y=2x2について，xの値が−1から3まで増加するときの変化の割合はである。 （長崎県2000年入試問題）
|
|
【例題２】
関数y=ax2について，xの値が1から4まで増加するときの変化の割合が−15であった。このとき，aの値を求めなさい。 （東京都2015年入試問題）
|
（解答） x=1のとき，y=a x=4のとき，y=16a 変化の割合は 5a=−15 a=−3 …（答） |
|
※以下に引用する高校入試問題で，元の問題は記述式の問題ですが，ｗｅｂ画面上で入力問題にすると操作性が悪いので，選択問題に書き換えています．
【問題２】 （画面上で解答するには，選択肢の中から正しいものを１つクリック）
(1)
関数y=x2で，xの値がaからa+2まで増加するときの変化の割合は4である。このとき，aの値を求めなさい。 （福井県2000年入試問題）
|
(2)
関数y=ax2について，xの値が−2から4まで変化するときの変化の割合を，aを用いて表しなさい。 （静岡県1999年入試問題）
|
|
(3)
関数y=ax2（aは定数）について，xの値が1から4まで変化するときの変化の割合は，xの値が0から1まで変化するときの変化の割合よりも2大きい。このとき，aの値を求めなさい。 （愛知県Ａ 1999年入試問題）
|
(4)
関数y=x2について，xの値が−1から2まで変化するときの変化の割合と，xの値が0からaまで変化するときの変化の割合が等しいとき，aの値を求めなさい。 |
...メニューに戻る
| 笆�縺薙�繧ｵ繧､繝亥�縺ｮGoogle讀懃ｴ｢笆� |