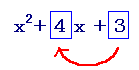|
【解説】 展開公式 (x+a)(x+b)=x2+(a+b)x+ab から 因数分解公式 x2+(a+b)x+ab=(x+a)(x+b) が導かれます. しかし,実際の問題は x2+(1+3)x+1·3 の形で示されることはめったになく,「x2+4x+3 を因数分解しなさい」の形で問われます. これを x2+4x+3=(x+1)(x+3) と変形するには, 和が 4 ,積が 3 となる2つの数を見つけることが重要です. 和が 4 ,積が 3 となる2つの数を見つけるには和と積のどちらを先に調べるとよいかを考えてみます. 【和が4となる数字を先に調べる場合】 2つとも整数として調べるとき,和が 4 になる組合せはたくさん(実は無限に)あるので,和から考えると大変です.
|
【積が3となる数字を先に調べる場合】 積が 3 になる整数の組は,少ないので積から調べると簡単です.
x2+4x+3=(x+1)(x+3) となります.
|