変化の割合

xの値が，3から5に変化したとき，
xの増加量は，5−3=2になります．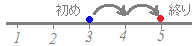

≪注意１≫
　増加量を考えるときは，必ず終りの値から初めの値を引きます．
　上の【例１】のような場合に，図の流れのままに3−5=−2としてしまう間違いが多いので，気をつけましょう．

日常用語では「減少量」が5
数学用語では「増加量」が−5

xの値が，7から2に変化したとき，
xの増加量は，2−7=−5になります．

≪注意２≫
　日常生活では「体重の増加量」「貯金の減少量」などと増加という用語も減少と言う用語もどちらも使いますが，数学では増加量が好んで使われ，減っているときはマイナスの値で示します．
⇒　値が減少していても増加量と言う

yの値が，−2から3に変化したとき，
yの増加量は，3−(−2)=5になります．

関数y=2x+1においてxの値が1から4まで変化するとき

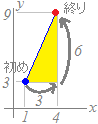
x=1のときy=3，x=4のときy=9だから
xの増加量は4−1=3
yの増加量は9−3=6

変化の割合は.

63n=2になります

「変化の割合」は（縦）÷（横）　
≪縦横とも±付き≫

関数y=−3x+2においてxの値が−1から4まで変化するとき

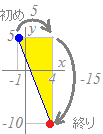
x=−1のときy=5
x=4のときy=−10だから
xの増加量は4−(−1)=5
yの増加量は−10−5=−15

変化の割合は.

−155nnn=−3になります

「変化の割合」は（縦）÷（横）
≪縦横とも±付き≫

計算と答を消す　⇒　OFF

計算と答を出す　⇒　ON

【傾きと変化の割合】
　１次関数y=ax+bについては，xの増加量が変わればyの増加量も変わるが，「変化の割合は，つねに傾きa」に等しい．

(A)　xが1から2まで変化するときの変化の割合
(B)　xが1から4まで変化するときの変化の割合

(A)

x	1 → 2
y	1 → 3

xの増加量
［横方向=］2−1=1
yの増加量
［縦方向=］3−1=2
変化の割合は（縦）÷（横）だから2÷1=2

(B)

x	1 → 4
y	1 → 7

xの増加量
［横方向=］4−1=3
yの増加量
［縦方向=］7−1=6
変化の割合は（縦）÷（横）だから6÷3=2

　上の例から分かるように，変化の割合はどこで測っても等しくなる．
○理由：右図のように１次関数は直線になるので，階段のように縦横の線で切りだすと，
（縦）÷（横）
は「相似図形の縦横の比」だからすべて等しくなる．
○（縦）÷（横）は「傾き」と呼ばれるので，「１次関数の変化の割合」は「直線の傾き」を表している．

　xがどこからどこまで変化するのか，yがどこからどこまで変化するのか，何も書いてないのにどうやって変化の割合を求めるのかと不思議に思った人は「そこそこよく考えている人」です．
　しかし，上には上があって，この問題では「どこで測っても同じになる」から，「xやyの変化する範囲が書いてなくても答が出る」ようになっています．
　自分で試しに，xの範囲を何通りか書いてみると，全部同じ答になることが分かります．

x	0 → 1
y	4 → 7

変化の割合は.

31n=3

x	1 → 3
y	7 → 13

変化の割合は.

62n=3

前の問題と同様に幾つか試してみると

x	0 → 1
y	5 → 1

変化の割合は.

−41nn=−4

x	1 → 3
y	1 → −7

変化の割合は.

−82nn=−4

(1)１次関数y=3x+4においてxの値が1から5まで変化するとき，変化の割合を求めてください．

1 2 3 4 5

解説

x=1のときy=7，x=5のときy=19だから
.xの増加量は5−1=4
.yの増加量は19−7=12

変化の割合は.

124nn=3

※（傾きに等しいから3と即答してもよい）

(2)１次関数y=−2x+3においてxの値が1から4まで変化するとき，変化の割合を求めてください．

−2 −1 0 1 2

解説

x=1のときy=1，x=4のときy=−5だから
.xの増加量は4−1=3
.yの増加量は−5−1=−6

変化の割合は.

−63nn=−2

※（傾きに等しいから−2と即答してもよい）

(3)反比例の関数y=.

12xnnにおいてxの値が2から6まで

変化するとき，変化の割合を求めてください．

−4 −1 1 4 12

解説

x=2のときy=6，x=6のときy=2だから
.xの増加量は6−2=4
.yの増加量は2−6=−4

変化の割合は.

−44nn=−1

※（反比例のグラフでは傾きは一定ではないので，反比例の式を見ただけで答える方法はない）

(4)反比例の関数y=−.

6xnにおいてxの値が1から3まで

変化するとき，変化の割合を求めてください．

−3 −2 1 2 3

解説

x=1のときy=−6，x=3のときy=−2だから
.xの増加量は3−1=2
.yの増加量は−2−(−6)=4

変化の割合は.

42n=2

※（反比例のグラフでは傾きは一定ではないので，反比例の式を見ただけで答える方法はない）

(5)１次関数y=−3x+2の変化の割合を求めてください．

−3 −2 1 2 3

解説

1次関数では，変化の割合は傾きに等しいから，−3

x=1からx=12まで変化するとき

x	1	→	12
y	12	→	1

変化の割合は $\frac{-11}{11}=-1$
これと等しくなるものを探します

x=1からx=4まで変化するとき

x	1	→	4
y	12	→	3

変化の割合は $\frac{-9}{3}=-3$
合わない

x=1からx=6まで変化するとき

x	1	→	6
y	12	→	2

変化の割合は $\frac{-10}{5}=-2$
合わない

x=2からx=3まで変化するとき

x	2	→	3
y	6	→	4

変化の割合は $\frac{-2}{1}=-2$
合わない

x=2からx=6まで変化するとき

x	2	→	6
y	6	→	2

変化の割合は $\frac{-4}{4}=-1$
≪合う≫…（答）

x=3からx=6まで変化するとき

x	3	→	6
y	4	→	2

変化の割合は $\frac{-2}{3}=-\frac{2}{3}$
合わない

髫ｨ�ｳ陋ｹ�ｺ隴ｫ螟撰ｿｽ�ｽ�ｽ驍ｵ�ｺ�ｽ�ｮ髯溷私�ｽ�｢驛｢�ｧ陋幢ｽｵ�ｽ�ｽ驍ｵ�ｺ�ｽ�ｦ驍ｵ�ｺ�ｽ�ｽ�ｽ邇厄ｽｫ�｢雋企ｳｶ�ｦ驍ｵ�ｺ�ｽ�ｯ髯ｷ闌ｨ�ｽ�ｨ鬯ｩ蟷｢�ｽ�ｨ鬮ｫ�ｱ�ｽ�ｭ驍ｵ�ｺ�ｽ�ｾ驍ｵ�ｺ陝ｶ蜷ｮﾂ�ｻ驛｢�ｧ郢ｧ�ｽ�ｽ閾･�ｸ�ｺ�ｽ�｣驍ｵ�ｺ�ｽ�ｦ驍ｵ�ｺ�ｽ�ｽ遶擾ｽｪ驍ｵ�ｺ陷ｻ�ｻ�ｽ�ｼ�ｽ�ｽ
髫ｨ�ｳ陋ｹ�ｺ隨渉髫ｲ�ｽ�ｽ�ｳ驍ｵ�ｺ�ｽ�ｮ髯ｷﾂ�ｽ�ｽ邵ｲ謚ｵ�ｿ�ｽ陟募ｨｯ�ｽ驍ｵ�ｺ�ｽ�ｮ髯懶ｿｽ陜楢ｶ｣�ｽ�｡陟募ｨｯﾂ�ｲ驍ｵ�ｺ�ｽ�ｩ驍ｵ�ｺ�ｽ�ｽ邵ｲ蝣､�ｸ�ｺ郢ｧ�ｽ螟｢驍ｵ�ｺ雋�ｼ会ｽｰ驛｢�ｧ陷ｻ闌ｨ�ｽ�ｭ�ｽ�｣鬩墓慣�ｽ�ｺ驍ｵ�ｺ�ｽ�ｪ髫ｴ�ｽ�ｿ�ｽ�ｽ�ｫ�ｽ�ｽ驍ｵ�ｺ�ｽ�ｧ髣費ｽｨ隴擾ｽｴ遶擾ｽｴ驍ｵ�ｺ�ｽ�ｦ驍ｵ�ｺ�ｽ�ｽ隨ｳ�ｽ�ｸ�ｺ�ｽ�ｽ驍ｵ�ｺ�ｽ�ｽ隨ｳ�ｽ�ｬ�ｾ�ｽ�ｹ髯懈ｻゑｽｿ�ｽ�ｽ�ｦ遶擾ｽｵ隰泌調�ｸ�ｺ�ｽ�ｫ髯晢ｿｽ�ｽ�ｾ驍ｵ�ｺ陷会ｽｱ遯ｶ�ｻ驍ｵ�ｺ�ｽ�ｯ�ｽ�ｽ隰疲ｺｷ�ｺ�ｽ螯呻ｿｽ�ｽ驍ｵ�ｺ�ｽ�ｪ鬯ｮ�ｯ髣企ｯ会ｽｽ鬘俶ｱ橸ｿｽ�ｾ髯滂ｽ｢隲帛ｲｩ�ｽ驛｢�ｧ闕ｵ譎｢�ｽ閧ｲ�ｸ�ｺ�ｽ�ｽ遶企豪�ｸ�ｺ陷会ｽｱ遯ｶ�ｻ驍ｵ�ｺ�ｽ�ｽ遶擾ｽｪ驍ｵ�ｺ陷ｻ�ｻ�ｽ�ｼ髮懶ｽ｣�ｽ�ｼ鬩包ｽｺ�つ�ｽ�ｻ驍ｵ�ｺ�ｽ�ｪ驍ｵ�ｺ陞ゑｿｽ�ｽ�ｼ隴ｴ�ｧ陋ｻ�､髫ｰ�ｦ�ｽ�ｽ陜趣ｽｪ驍ｵ�ｺ�ｽ�ｪ髫ｴ�ｽ�ｿ�ｽ�ｽ�ｫ�ｽ�ｽ驍ｵ�ｺ�ｽ�ｫ驍ｵ�ｺ�ｽ�ｪ驍ｵ�ｺ�ｽ�｣驍ｵ�ｺ�ｽ�ｦ驍ｵ�ｺ�ｽ�ｽ�ｽ邇匁捗�ｽ�ｴ髯ｷ�ｷ陋ｹ�ｻ�ｽ�ｽ�ｽ�ｽ陟募ｨｯ關ｽ驛｢�ｧ陟暮ｯ会ｽｽ螳壽ｦ�ｽ�ｬ鬯ｮ�｢闕ｵ譏ｶ�ｽ驛｢�ｧ闕ｵ譏ｶ�ｽ鬩包ｽｲ�ｽ�ｽ�つ�ｽ�ｽ隨�ｽ｡驍ｵ�ｺ闔会ｽ｣邵ｲ蝣､�ｸ�ｺ�ｽ�ｪ驍ｵ�ｺ陷托ｽｰ�ｽ�ｪ�ｽ�ｭ鬮｢�ｽ�ｽ�ｽ�ｽ繧句擅�ｽ�ｭ驛｢�ｧ�つ驍ｵ�ｺ髦ｮ蜷ｮ�ｽ驍ｵ�ｺ�ｽ�ｫ驍ｵ�ｺ�ｽ�ｪ驛｢�ｧ驗呻ｽｫ遶擾ｽｪ驍ｵ�ｺ陷ｷ�ｶ�ｽ�ｽ驍ｵ�ｺ�ｽ�ｧ�ｽ�ｽ隴ｴ�ｧ雎撰ｽｻ鬨ｾ蛹�ｽｽ�ｨ驍ｵ�ｺ陷会ｽｱ遶擾ｽｪ驍ｵ�ｺ陝ｶ蜻ｻ�ｽ髮｣�ｿ�ｽ髮懶ｽ｣�ｽ�ｼ�ｽ�ｽ