直線の平行条件

== 直線の平行条件 ==

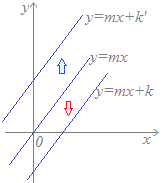
《解説》
　y=mx+k…(2)
のグラフは，
y=mx…(1)
のグラフをy軸方向に平行移動したものです．（k>0ならば上に，k<0ならば下に平行移動したものです．）

y=mx+k'…(3)
のグラフも，
y=mx…(1)
のグラフをy軸方向に平行移動したものです．

　だから，y=mx+kのグラフとy=mx+k'のグラフは互いに平行です．（特に，k=k'の場合は，２つの直線は一致します．）

【要点】
　２つの直線
y=mx+k
y=mx+k'
は，傾きmが等しければ平行になる．
（切片の値k, k'は平行かどうかに関係ない）

【例】

(1)
　y=2x+3
　y=2x+4
は，いずれも傾きが2に等しいから平行です．

(2)
3x+5y=1→ $y=-\frac{3}{5}x+ \frac{1}{5}$
3x+5y=2→ $y=-\frac{3}{5}x+ \frac{2}{5}$

は，いずれも傾きが $-\frac{3}{5}$ に等しいから平行です．

(3)
　y=2x+3
　y=−2x+4
は，いずれも傾きが等しくないので平行ではありません．

(4)
3x+5y=1→ $y=-\frac{3}{5}x+ \frac{1}{5}$
3x+4y=1→ $y=-\frac{3}{4}x+ \frac{1}{4}$
は，傾きが等しくないので平行ではありません．

《問題》
　次のうち，平行な直線を選びなさい．
○初めに左欄の方程式一つクリックし，続けてこれと平行な直線を右欄からクリックしたとき，合っていれば消えます．間違えば消えません．
○間違ったときは，右の欄を連打してもやり直しにはなりません．
○間違ったときは，「HELP」と「再開する」のボタンが表示されます．「HELP」を見る場合でも見ない場合でも「再開する」ボタンを押せば解答を続けることができます．

HELP 再開する

$2x-y+ 1=0$ すなわち $y=2x+ 1$ の傾きは2です 3x+y=0すなわちy=−3xの傾きは−3です 8x−2y=7すなわち $y=4x+ \frac{7}{2}$ の傾きは4です y=−xの傾きは−1です $y=\frac{1}{2}x+ 1$ の傾きは $\frac{1}{2}$ です 2x−5y+1=0すなわち $y=\frac{2}{5}x+ \frac{1}{5}$ の傾きは $\frac{2}{5}$ です 3x−y−1=0すなわちy=3x−1の傾きは3です y−x+1=0すなわちy=x−1の傾きは1です $y=-\frac{1}{2}x$ の傾きは $-\frac{1}{2}$ です 4(x−2)=3(y−1)すなわち $y=\frac{4}{3}x-\frac{5}{3}x$ の傾きは $\frac{4}{3}$ です y=2x+3の傾きは2です y=1−3x=−3x+1の傾きは−3です y=4x−3の傾きは4です 3x+3y=1すなわち $y=-x + \frac{1}{3}$ の傾きは−1です 2x−4y+3=0すなわち $y=\frac{1}{2}x+ \frac{3}{4}$ の傾きは $\frac{1}{2}$ です 2x−5y−3=0すなわち $y=\frac{2}{5}x-\frac{3}{5}$ の傾きは $\frac{2}{5}$ です y=2+3x=3x+2の傾きは3です x−y=2すなわちy=x−2の傾きは1です 2(1−y)=x+3すなわち $y=-\frac{1}{2}x-\frac{1}{2}$ の傾きは $-\frac{1}{2}$ です 4x−3y=1すなわち $y=\frac{4}{3}x-\frac{1}{3}$ の傾きは $\frac{4}{3}$ です傾きが等しい組合せを選ばなければなりません