集合の表し方（オイラー図）

→ 携帯版は別頁

このページのバックアップ・ページ
（グーグルブロガー版）は，こちら⇒

== 集合の表し方（オイラー図） ==

[1]集合の表し方

【問題１】　次の集合を「要素を書き並べる方法」で表すとき，正しいものを下の選択肢から選んでください．（正しいものをクリック）
ただし，Nは自然数全体の集合，Zは整数全体の集合とする．

(1)
$\{x\mid -3\lt x\lt 3,\hspace{5}x\in Z \}$

解説やり直す

$\{1,\hspace{5}2 \}$ $\{0,\hspace{5}1,\hspace{5}2 \}$ $\{1,\hspace{5}2,\hspace{5}3 \}$

$\{-2,-1,\hspace{5}0,\hspace{5}1,\hspace{5}2 \}$ $\{-3,-2,-1,\hspace{5}0,\hspace{5}1,\hspace{5}2,\hspace{5}3 \}$

$x\in Z$

「 $x$ は整数全体の集合に含まれている」
すなわち「 $x$ は整数」

$-3\lt x \lt 3$

$x$ は−3よりも大きくて（−3は含まない）3よりも小さい（3は含まない）

$\{-2,-1,\hspace{5}0,\hspace{5}1,\hspace{5}2 \}$ …（答）

→閉じる←

(2)
$\{n\hspace{5}\mid\hspace{5} n=2m+ 1,\hspace{5}0\underline{\le} m \underline{\le}3,\hspace{5} m\in Z \}$

解説やり直す

$\{1,\hspace{5}2,\hspace{5}3 \}$ $\{0,\hspace{5}1,\hspace{5}2,\hspace{5}3 \}$

$\{1,\hspace{5}3,\hspace{5}5,\hspace{5}7 \}$ $\{3,\hspace{5}5,\hspace{5}7,\hspace{5}9 \}$

$x\in Z$

$m$ は整数

$0\underline{\le} m \underline{\le}3$

$m$ は0以上3以下

その $0\underline{\le} m \underline{\le}3$ を用いて

$n=2m+ 1$ で定義される $n$ は
$m=0$ のとき $n=1$
$m=1$ のとき $n=3$
$m=2$ のとき $n=5$
$m=3$ のとき $n=7$

これらの $n$ を要素とする集合だから $\{1,\hspace{5}3,\hspace{5}5,\hspace{5}7 \}$ …（答）

→閉じる←

(3)
$\{n^2\hspace{5}\mid\hspace{5} n$ は $6$ の約数 $,\hspace{5}n\in N\}$

解説やり直す

$\{1,\hspace{5}2,\hspace{5}3 \}$ $\{1,\hspace{5}2,\hspace{5}3,\hspace{5}6 \}$

$\{1,\hspace{5}4,\hspace{5}9,\hspace{5}36 \}$ $\{1,\hspace{5}2,\hspace{5}3,\hspace{5}4,\hspace{5}5,\hspace{5}6 \}$

$n\in N$

$n$ は自然数（正の整数）で $6$ の約数だから
$n=1,\hspace{5}2,\hspace{5}3,\hspace{5}6$

その $n$ を用いて

$n^2$ で定義される数は
$n=1$ のとき $n^2=1$
$n=2$ のとき $n^2=4$
$n=3$ のとき $n^2=9$
$n=6$ のとき $n^2=36$

これらの $n^2$ を要素とする集合だから $\{1,\hspace{5}4,\hspace{5}9,\hspace{5}36 \}$ …（答）

→閉じる←

→右上に続く

【問題２】　次の集合を「要素と条件で表す方法」で書くとき，正しいものを下の選択肢から選んでください．（正しいものをクリック）
ただし，Nは自然数全体の集合，Zは整数全体の集合とする．

(1)
$\{2,\hspace{5}4,\hspace{5}6,\hspace{5}8 \}$

解説やり直す

$\{n\hspace{5}\mid \hspace{5}2\underline{\le}n\underline{\le}8, \hspace{5}n\in N \}$

$\{n\hspace{5}\mid \hspace{5}1\underline{\le}n\underline{\le}4, \hspace{5}n\in N \}$

$\{n\hspace{5}\mid\hspace{5} n=2m,\hspace{5}1\underline{\le}m\underline{\le}4, \hspace{5}m\in N \}$

$\{2n\hspace{5}\mid \hspace{5}2\underline{\le}n\underline{\le}8, \hspace{5}n\in N \}$

$\hspace{5}2\underline{\le}n\underline{\le}8, \hspace{5}n\in N$

すなわち $n$ を２以上８以下の自然数とすると
$\{2,3,4,5,6,7,8\}$ になって元の問題と合わない

$\hspace{5}1\underline{\le}n\underline{\le}4, \hspace{5}n\in N$

すなわち $n$ を１以上４以下の自然数とすると
$\{1,2,3,4\}$ になって元の問題と合わない

$\hspace{5}1\underline{\le}m\underline{\le}4, \hspace{5}n\in N$

すなわち $m$ を１以上４以下の自然数とすると
$\{1,2,3,4\}$ になり，
その $m$ を用いて $n=2m$ と書ける数 $n$ の集合は
$\{2,4,6,8\}$ となって元の問題と合う…（答）

$\hspace{5}2\underline{\le}n\underline{\le}8, \hspace{5}n\in N$

すなわち $n$ を２以上８以下の自然数とすると
$\{2,3,4,5,6,7,8\}$ になり
その $n$ を用いて $2n$ と書ける数の集合は
$\{4,6,8,10,12,14,16\}$ になって元の問題と合わない

→閉じる←

(2)
$\{1,\hspace{5}\frac{1}{2},\hspace{5}\frac{1}{3} \}$

解説やり直す

$\{n\hspace{5}\mid \hspace{5}\frac{1}{3}\underline{\le}n\underline{\le}1, \hspace{5}n\in N \}$

$\{\frac{1}{n}\hspace{5}\mid \hspace{5}1\underline{\le}n\underline{\le}3, \hspace{5}n\in N \}$

$\{x\hspace{5}\mid\hspace{5} x=\frac{1}{m},\hspace{5}1\underline{\le}m\underline{\le}4, \hspace{5}m\in N \}$

$\{x\hspace{5}\mid \hspace{5}1\underline{\le}n\underline{\le}3, \hspace{5}n\in \frac{1}{N} \}$

$\frac{1}{3}\underline{\le}n\underline{\le}1, \hspace{5}n\in N$

すなわち $n$ を $\frac{1}{3}$ 以上 $1$ 以下の自然数とすると
$\{1\}$ だけになって元の問題と合わない

$1\underline{\le}n\underline{\le}3, \hspace{5}n\in N$

すなわち $n$ を１以上３以下の自然数とすると
$\{1,2,3\}$ になり，
その $n$ を用いて $\frac{1}{n}$ と書ける数の集合は
$\{1,\hspace{5}\frac{1}{2},\hspace{5}\frac{1}{3}\}$ となって元の問題と合う…（答）

$\hspace{5}1\underline{\le}m\underline{\le}4, \hspace{5}m\in N$

すなわち $m$ を1以上4以下の自然数とすると
$m=1,2,3,4$ になり

その $m$ を用いて $x=\frac{1}{m}$ で定義されると書ける数の集合は $\{1,\hspace{5}\frac{1}{2},\hspace{5}\frac{1}{3},\hspace{5}\frac{1}{4}\}$ になって元の問題と合わない

$\frac{1}{N}$

通常は集合で割るような記号は定義されていない

→閉じる←

(3)
$\{1,\hspace{5}2,\hspace{5}3,\hspace{5}6 \}$

解説やり直す

$\{n\hspace{5}\mid \hspace{5}\frac{6}{n}\in N,\hspace{5}n\in N \}$

$\{n\hspace{5}\mid \hspace{5}\frac{n}{6}\in N,\hspace{5}n\in N \}$

$\{n\hspace{5}\mid\hspace{5} n=\frac{m}{6},\hspace{5}m\in N \}$

$\{n\hspace{5}\mid \hspace{5}n=6m,\hspace{5}m\in N\}$

$\frac{6}{n}\in N,\hspace{5}n\in N$

すなわち $n$ が自然数で $\frac{6}{n}$ も自然数になるのだから $n$ は $6$ の約数．元の問題と合う…（答）

$\frac{n}{6}\in N,\hspace{5}n\in N$

すなわち $n$ が自然数で $\frac{n}{6}$ も自然数になるのだから $n$ は $6$ の倍数．
$\{6,12,18,\cdots \}$ となって元の問題と合わない

$m\in N$

すなわち $m$ が自然数であるとき，その $m$ を用いて $n=\frac{m}{6}$ で定義される $n$ は
$\{\frac{1}{6},\frac{2}{6},\frac{3}{6},\frac{4}{6},...\}$ となって元の問題と合わない

$m\in N$

すなわち $m$ が自然数であるとき，その $m$ を用いて $n=6m$ で定義される $n$ は
$\{6,12,18,...\}$ となって元の問題と合わない

→閉じる←

[2]オイラー図（またはベン図）の読み方

【問題３】　次の図で表される集合について，次の記号で表されるものを下の選択肢から選んでください．（正しいものをクリック）

(1)
$A\cap B\cap C$

解説やり直す

P Q R S

T V X Y

AにもBにもCにも含まれているのはR

→閉じる←

(2)
$\bar{A}\cap B\cap C$

解説やり直す

P Q R S

T V X Y

Aの外側でBの内側でCの内側はV

→閉じる←

(3)
$A\cap(\bar{B\cup C})$

解説やり直す

P Q R S

T V X Y

まずB∪Cの外側にあるもの $\bar{B\cup C}$ を考えるとPとY
そのうちでAの内側にあるものはP

→閉じる←

→右上に続く

【問題４】　次の図で表される集合について，次の集合に等しいものを下の選択肢から選んでください．（正しいものをクリック）

(1)
$R\cup S$

解説やり直す

$A\cap B\cap C$ $A\cap B$ $A\cap C$ $B\cap C$

$A\cap C$ はRとSになる

→閉じる←

(2)
$Q\cup R\cup S$

解説やり直す

$A\cup B\cup C$ $A\cap (B \cup C)$

$B\cap (C \cup A)$ $C\cap (A \cup B)$

$A\cup B\cup C$ はY以外の全部が入るから広過ぎる．

$A\cap (B\cup C)$ を考えるために，まず $B\cup C$ を考えるとQ,R,S,T,V,X
そのうちでAの内側にあるのはQ,R,S $A\cap (B\cup C)$ …（答）

同様にして $B\cap (C\cup A)=Q\cup R\cup V$ は違う

同様にして $C\cap (A\cup B)=R\cup S\cup V$ は違う

→閉じる←

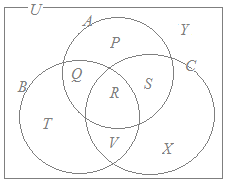
[3]オイラー図（またはベン図）を用いた推論の仕方

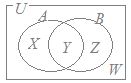
　右の図を利用するとすべての場合の $A,B$ の関係を調べることができる．
　例えば $X=\emptyset$ とすれば $A\subset B$ の場合を表すことができ，
$Z=\emptyset$ とすれば $A\supset B$ の場合を表すことができ，
$Y=\emptyset$ とすれば $A\cap B=\emptyset$ の場合を表すことができる．
　このように， $A,B$ の包含関係（どちらがどちらを含んでいるか，共通部分があるかないかなど）は，問題に応じて右図のX, Y, Z, Wのうちいくつかが「ない」（空集合）だとすればよい．

【例題】
$A\cup B\subset B$
が成り立つのはどのような場合か

右図において $A\cup B$ はX, Y, Z

次に， $B$ はY, Z

$A\cup B\subset B$ となるのはXの部分がない場合
これは， $A\subset B$ の場合と言ってもよい．

【問題５】　次の各々の関係式について，

[1] つねに成り立つ　
[2] 成り立つ場合と成り立たない場合がある　
[3] 絶対に成り立たない

の中から正しいものを選んでください（選択肢をクリック）．

(1)
$\bar{A\cap B}=\bar{A}\cap \bar{B}$

解説やり直す

[1] つねに成り立つ

[2] 成り立つ場合と成り立たない場合がある

[3] 絶対に成り立たない

右図において $A\cap B$ は $Y$ だから， $\bar{A\cap B}$ は $X,Z,W$

右辺の $\bar{A}\cap \bar{B}$ は $W$

したがって， $X=\emptyset$ かつ $Z=\emptyset$ の場合，すなわち $A=B$ のとき等号が成り立つ．そうでなければ成り立たない．→[2]

→閉じる←

(2)
$\bar{A\cup B}=\bar{A}\cap \bar{B}$

解説やり直す

[1] つねに成り立つ

[2] 成り立つ場合と成り立たない場合がある

[3] 絶対に成り立たない

$A\cup B$ は $X,Y,Z$ だから， $\bar{A\cup B}$ は $W$

右辺の $\bar{A}\cap \bar{B}$ は $W$

したがって，つねに等しい．→[1] （※この関係は２つあるド・モルガンの法則の１つになっている）

→閉じる←

→右上に続く

(3)
$A\cap B\supset A$

解説やり直す

[1] つねに成り立つ

[2] 成り立つ場合と成り立たない場合がある

[3] 絶対に成り立たない

右図において $A\cap B$ は $Y$

右辺の $A$ は $X,Y$

したがって， $X=\emptyset$ の場合，すなわち $A\subset B$ のとき成り立つ．そうでなければ成り立たない．→[2]

→閉じる←

(4)
$A\cap B=A$ ならば $A\cup B=B$

解説やり直す

[1] つねに成り立つ

[2] 成り立つ場合と成り立たない場合がある

[3] 絶対に成り立たない

右図において $A\cap B$ は $Y$
これが $A$ に等しいのだから $X=\emptyset$

このとき， $A\subset B$ は成り立つ．→[1]

→閉じる←

(5)
$A\cap B=A\cup B$ ならば $A=B$

解説やり直す

[1] つねに成り立つ

[2] 成り立つ場合と成り立たない場合がある

[3] 絶対に成り立たない

右図において $A\cap B$ は $Y$

$A\cup B$ は $X,Y,Z$

これらが等しいのだから， $X=Z=\emptyset$
したがって $A=B$ は成り立つ．→[1]

→閉じる←

○===メニューに戻る

■［個別の頁からの質問に対する回答］[集合の表し方（オイラー図）について／17.7.7］

集合とオイラー図の理解が進みました。ありがとうございました。 PC版頁の問題2の(2)についてですが、解説文の中で"1≦m≦4"とすべきところが"1≦m≦3"になっていたり"mを1以上3以下の自然数とするとm=1,2,3,4になり"という誤記があったり、選択肢はxになっている箇所の解説がnになっていたり複数の誤記があるようです
＝＞［作者］：連絡ありがとう．確かに，疲労がたまって，誤記があったようです．

■［個別の頁からの質問に対する回答］[集合の表し方（オイラー図）について／17.1.29］

問題２の（２）で正しい答え（上から二番目）を選択しても×となるが、解説には上から二番目が正解と書いてある。
＝＞［作者］：連絡ありがとう．昨日アップしたばかりで，トラブルは初期に起こるのお決まりのコースのようで．訂正しました．