|
�i�T�j�@���߂�x2�̌W�������ɂȂ��Ă���2���s�����́C���ӂɁ|�P���|���āCx2�̌W�������ɂȂ�悤�ɏ��������܂��D 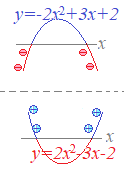 x2�̌W�������ɂȂ��Ă���2���s�����C�Ⴆ��
x2�̌W�������ɂȂ��Ă���2���s�����C�Ⴆ��−2x2+3x+2<0 �̂悤�Ȗ����u���̂܂܉������Ƃ���Ɓv y=−2x2+3x+2 �Ƃ�����ɓʂ̃O���t��`���āCy<0�ɂȂ�悤��x�̒l�͈̔͂�T���Ȃ���Ȃ�Ȃ����ƂɂȂ�܂��D ���̂悤�Ȗ��́C���̕s������ 2x2−3x−2>0 �ɕό`���Ă���������ƂɌ��߂Ă����ƁC���x2�̌W�������� y=2x2−3x−2 �Ƃ����u�悭�����ꂽ�v�O���t�ʼn�����悤�ɂȂ�܂��D �����ŁC�ȉ��ɂ����Ă�x2�̌W�������ɂȂ��Ă���2���s�������o�ꂵ����C���ӂɁ|�P���|���āCx2�̌W�������ɂȂ�悤�ɏ��������ĉ������Ƃɂ��܂��D
y=ax2+bx+c�ɂ����ĂQ���̌W��a�����ł���Ƃ��A�O���t�͒J�`�ɂȂ�܂��B
�ˁ@y=ax2+bx+c�i�������Ca>0�j�͒J�` �i�U�j x2�̌W��������
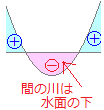
�A�jax2+bx+c=0�̉���x=α, β ( α<β )
�̂Ƃ�
(1) ��肪ax2+bx+c<0 (a>0)�Ȃ�C
����
α<x<β
�}�C�i�X�́u�ԁv (2) ��肪ax2+bx+c>0 (a>0)�Ȃ�C 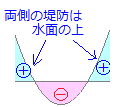
����
x<α, β<x
�v���X�́u�����v (3) ��肪ax2+bx+c��0 (a>0)�Ȃ�C 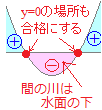
����α��x��β
�}�C�i�X�́u�ԁv �����t�� (4) ��肪ax2+bx+c��0 (a>0)�Ȃ�C 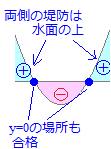
����x��α, β��x
�v���X�́u�����v �����t�� |
|
�C�jax2+bx+c=0�̉���x=α�i�d���j
�̂Ƃ�
(1) ��肪ax2+bx+c<0 (a>0)�Ȃ�C
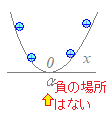
����
���Ȃ� (2) ��肪ax2+bx+c>0 (a>0)�Ȃ�C 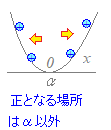
����x<α, α<x
�ix��α�ł��悢�j (3) ��肪ax2+bx+c��0 (a>0)�Ȃ�C 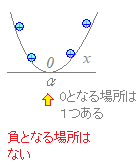
����x=α
(4) ��肪ax2+bx+c��0 (a>0)�Ȃ�C 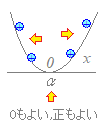
���́u���ׂĂ̎����v
|
|
�E�jax2+bx+c=0���������������Ȃ��Ƃ�
(1) ��肪ax2+bx+c<0 (a>0)�Ȃ�C
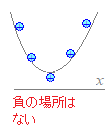
����
���Ȃ� (2) ��肪ax2+bx+c>0 (a>0)�Ȃ�C 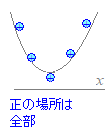
����
���ׂĂ̎��� (3) ��肪ax2+bx+c��0 (a>0)�Ȃ�C 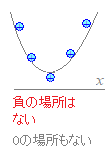
����
���Ȃ� (4) ��肪ax2+bx+c��0 (a>0)�Ȃ�C 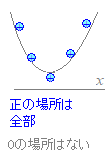
����
���ׂĂ̎��� |