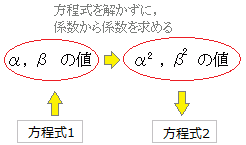
【例３】
実数p, qに対し， x3−px+q=0の解がすべて実数なら（すなわち虚数解を持たないなら）， x3−2px2+p2x−q2=0の解もすべて実数であることを示せ．
（京都大学）
（解説）
x3−px+q=0の解をα,β,γ（実数）とすると，解と係数の関係により
α+β+γ=0
αβ+βγ+γα=−p
αβγ=−q
このとき
α2+β2+γ2=(α+β+γ)2−2(αβ+βγ+γα)=2p
α2β2+β2γ2+γ2α2=(αβ+βγ+γα)2−2αβγ(α+β+γ)=p2
α2β2γ2=(αβγ)2=q2
だから，α2, β2, γ2を解とする３次方程式（のうちでx3の係数が1であるもの）は
x3−2px2+p2x−q2=0
となる．
この方程式の解は，α2, β2, γ2だから実数になる．
≪なぜα2, β2, γ2を思いつくのか？≫
上のように答案を示されると，何の抵抗もないが，なぜα2, β2, γ2を思いつくのか？ということはむずかしい．
定数項が−q2となることから−(αβγ)2すなわちα2, β2, γ2を解とする３次方程式を”試してみる”くらいかな～
実際には，α,β,γの対称式は基本対称式：α+β+γ, αβ+βγ+γα, αβγで表されるが，そうでなければ表されるとは限らないので，とりあえず対称式の組αβ, βγ, γαを”試してみて”，当たればよかったという進め方が考えられます．
数学でも因数分解の係数決めなど「まぐれ当たり」「当てもん」的なやり方が必要なものは，他でもあります．
|
【問題５】
２次方程式x2+ax+b=0の解をα, βとするとき，２次方程式x2+(a+2)x+(a+b+1)=0の解は，次のどれに対応しますか．
1α−1, β−1
2α+1, β+1
32α−1, 2β−1
42α+1, 2β+1
HELP
x2+ax+b=0についての解と係数の関係から
α+β=−a
αβ=b
(1) α−1, β−1を解とする２次方程式について調べると
(α−1)+(β−1)=(α+β)−2=−a−2
(α−1)(β−1)=αβ−(α+β)+1=b+a+1
方程式は
x2+(a+2)x+(a+b+1)=0 → 対応する
(2) α+1, β+1を解とする２次方程式について調べると
(α+1)+(β+1)=(α+β)+2=−a+2
(α+1)(β+1)=αβ+(α+β)+1=b−a+1
方程式は
x2+(a−2)x+(b−a+1)=0 → 対応しない
(3) 2α−1, 2β−1を解とする２次方程式について調べると
(2α−1)+(2β−1)=2(α+β)−2=−2a−2
(2α−1)(2β−1)=4αβ−2(α+β)+1=4b+2a+1
方程式は
x2+(2a+2)x+(4a+2b+1)=0 → 対応しない
(4) 2α+1, 2β+1を解とする２次方程式について調べると
(2α+1)+(2β+1)=2(α+β)+2=−2a+2
(2α+1)(2β+1)=4αβ+2(α+β)+1=4b−2a+1
方程式は
x2+(2a−2)x+(4b−2a+1)=0 → 対応しない
→1
|
【問題６】
３次方程式ax3+bx2+c=0 (a≠0)の解をα,β,γとするとき，３次方程式a2x3+bcx−c2=0 (a≠0)の解は，次のどれに対応しますか．
1α−1, β−1, γ−1
2α+1, β+1, γ+1
3αβ, βγ, γα
4α2, β2, γ2
HELP
ax3+bx2+c=0 (a≠0)の解を α,β,γ（実数）とすると，解と係数の関係により
α+β+γ=−. ban
αβ+βγ+γα=0
αβγ=−.can
(1) α−1, β−1, γ−1を解とする３次方程式について調べると
(α−1)+(β−1)+(γ−1)=(α+β+γ)−3=−.ban−3
(α−1)(β−1)+(β−1)(γ−1)+(γ−1)(α−1)
=(αβ+βγ+γα)−2(α+β+γ)+3=.2bann+3
(α−1)(β−1)(γ−1)
=αβγ−(αβ+βγ+γα)+(α+β+γ)−1=−.can−.ban−1
方程式は
x3+(.ban+3)x2+(.2bann+3)x+(.can+.ban+1)=0
ax3+(b+3a)x2+(2b+3a)x+(a+b+c)=0 → 対応しない
同様にして(2)(4)も対応しない
(3) αβ, βγ, γαを解とする３次方程式について調べると
αβ+βγ+γα=0
αββγ+βγγα+γααβ=αβγ(α+β+γ)=(−.can)(−.ban)=.bca2nn
αββγγα=(αβγ)2=.c2a2n
方程式は
x3+.bca2nnx−.c2a2n=0
a2x3+bcx−c2=0 → 対応する
→3
|
【問題７】
実数a,b,cに対し， x3+ax2+bx+c=0の３つの解がすべて正の実数であるとき， x3−bx2+acx−c2=0の解について，次のうちで正しいものを選んでください．ただし，二重解は２つと数え，三重解は３つと数えるものとします．
1１つは正の実数で２つは負の実数
2２つは正の実数で１つは負の実数
3３つとも正の実数
4１つは実数で２つは虚数
HELP
x3+ax2+bx+c=0の解を α>0,β>0,γ>0（実数かつ正）とすると，解と係数の関係により
α+β+γ=−a
αβ+βγ+γα=b
αβγ=−c
αβ, βγ, γαを解とする３次方程式について調べると
αβ+βγ+γα=b
αββγ+βγγα+γααβ=αβγ(α+β+γ)=(−c)(−a)=ac
αββγγα=(αβγ)2=c2
方程式は
x3−bx2+acx−c2=0
この方程式の解は αβ>0, βγ>0, γα>0だから３つとも正の実数
→3
なぜαβ,βγ,γαを思いつくのか？ということを説明するのは難しい．
いろいろ試してみたら，当たったということで･･･
|
...�域声蟶ｯ迚茨ｼ峨Γ繝九Η繝ｼ縺ｫ謌ｻ繧�