無限級数

【用語】

（有限）数列 a1,a2,a3,···,an	（有限）数列の和 a1+a2+a3+···+an
無限数列 a1,a2,a3,···,an,···	無限級数 a1+a2+a3+···+an+··· 無限級数の和

　「数列」を加えたものを「数列の和」というのは，わかりやすい対応関係ですが，「無限数列」を前から順に加えて行ったものは，「無限級数」と呼ばれる．
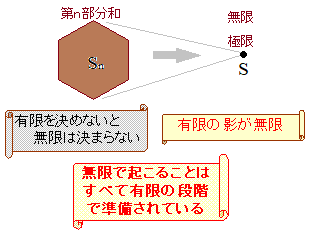
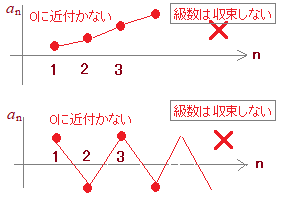
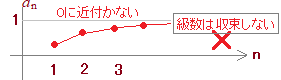
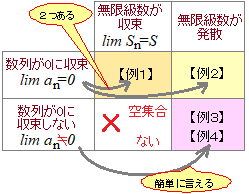
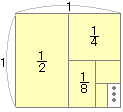
（＃1つ目の落とし穴）
　「無限級数」と「無限級数の和」の対応関係は，「数列」と「数列の和」の関係と同じではない．
　結論から言えば，無限級数が収束するときその値を無限級数の和という．無限級数を「さらに足す」訳ではない．
無限級数が収束しないとき，無限級数は発散するという．
（＃2つ目の落とし穴）
　今の高校の教科書では，級数という用語は無限と言う用語と一緒に使われる．（無限等比級数という用語はある）
　しかし，高卒では「テイラー級数」「フーリエ級数」「超幾何級数」のように級数だけで用いられる用語も多数ある．内容的に，これらはすべて無限級数を表している．要するに，級数と言えば無限級数のことになる．
（＃3つ目の落とし穴）
　小学校以来，足し算はどの順に加えてもかまわないという暗黙の前提を使って計算してきた．実際，有限数列の和を求めるときは，どの順に加えても同じ値になる．
　しかし，無限が入ってくると事情が一変する．無限個のものの和は足す順序によって変わることがあり，無限級数の和を求めるときに，足し算の順序を勝手に変えてはいけない．

【足し算の順序を変えてはいけないことを示す例】
求めたいもの：1−1+1−1+1−1+···
■２つずつ先に足すと：(1−1)+(1−1)+(1−1)+···
=0+0+0+···=0…①
■先頭以外の２つずつを足すと：
1+(−1+1)+(−1+1)+(−1+1)+···
=1+0+0+···=1…②

①②のように足す順序を変えると異なる値になる．（後で詳しく述べるが）正しくは次のように行う．
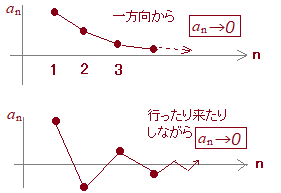
S1=1 , S2=1−1=0, S3=1−1+1=1, S4=1−1+1−1=0 , …
となるから，奇数番目まで足すと1になり，偶数番目まで足すと0になるので，どこまで行っても１つの値に近付かないから，「発散する」「和はない」

■1/2になるようなインチキ答案も書けます：
S=1−1+1−1+1−1+···とおくと
（↑↑これが間違い：実はこの和は定数にならない）
1−S=1−(1−1+1−1+1−1+···)
=1−1+1−1+1−1+···=Sとなるから
1=2S
$S=\frac{1}{2}$ …③

■別の例であるが，次の例はもっと異常さが目立つので，注意を促せる．
S=1+2+4+8+···…④とおくと
（↑↑初めから間違っている．この和は定数にならない）
2S=2+4+8+···…⑤
④−⑤
−S=1
S=−1（正の数ばかり足しているのに，和が負）

【無限級数の和】
無限級数
a1+a2+a3+···+an+··· …(1)
の第ｎ項までの和
Sn=a1+a2+a3+···+an …(2)
を「第ｎ部分和」（教科書では，「第ｎ項までの部分和」）という．

S1=a1
S2=a1+a2
S3=a1+a2+a3
… …
Sn=a1+a2+a3+···+an

このようにして作った第ｎ部分和の数列(2)が収束するとき，その極限値Sを無限級数(1)の和という．
第ｎ部分和の数列Snが収束しないとき，無限級数(1)は発散するという．

次の記号を用いる．

≪第ｎ部分和≫：(2)式
$S_n=\sum_{k=1}^na_k$

≪無限級数の和≫：(1)式
$\lim_{n\rightarrow\infty}S_n=\lim_{n\rightarrow\infty}\sum_{k=1}^na_k=S$ …(1.1)
または
$\lim_{n\rightarrow\infty}S_n=\sum_{n=1}^{\infty}a_n=S$ …(1.2)

(1.1)では末項を表す文字ｎとΣ記号の内部変数とがもつれないように，ｎ以外の文字：例えばｋを使って内部変数を表す．
(1.2)ではΣ記号の初項（1），末項（∞）とも定数・記号で，変数がもつれるおそれはないから，一般項の変数としてｎが使える．もちろん， $\sum_{k=1}^{\infty}a_k$ でもよいが，実際にそう書いている教科書は見たことがない．（整数を表す変数は，特に事情がなければｎで書くのが自然．）

　高校数学Ⅲ大手3社（S社，T社，K社）の教科書には，次の例1，例2の問題が全く同じように出ています（解説文は少しずつ異なります）．これらの問題は「第ｎ部分和が式として示せる」「収束する例と発散する例の２つ示せる」という点で，入門段階で取り上げるには実に最適な問題だと考えられます．
　当教材にこれらの問題をそのまま転記すると，著作権的にどうなのかというグレーゾーンの疑いが脳裏をよぎりますが，昭和30年代の参考書（当時の数ⅡB）から見ても長い間解説用に重宝されてきたことがうかがえるので，当教材でも例として使います．（これ以上やさしい例を他に見つけにくいので，解説の語句で独自性を目指します．管理人は理屈っぽい性格らしい）

【例１】　次の無限級数の和を求めてください．
$\frac{1}{1\cdot 2}+\frac{1}{2\cdot 3}+\frac{1}{3\cdot 4}+\cdots+\frac{1}{n(n+ 1)}+\cdots$

（解答）
第ｎ部分和は
$S_n=\frac{1}{1\cdot 2}+\frac{1}{2\cdot 3}+\frac{1}{3\cdot 4}+\cdots+\frac{1}{n(n+ 1)}$
$=\hspace{10}(\frac{1}{1}-\cancel{\frac{1}{2}})$

第ｎ部分和（有限数列の和）では，どの順に足したり引いたりしても結果は変わらない

$+(\cancel{\frac{1}{2}}-\cancel{\frac{1}{3}})$
$+(\cancel{\frac{1}{3}}-\cancel{\frac{1}{4}})$
$+\cdots\hspace{3}\cdots$
$+(\cancel{\frac{1}{n}}-\frac{1}{n+ 1})$
$=1-\frac{1}{n+ 1}$
だから
$\lim_{n\rightarrow \infty}S_n=\lim_{n\rightarrow \infty}(1-\frac{1}{n+ 1})=1$
したがって，この無限級数は収束し，その和は1である．

【要点】
■いきなり無限を考えるのは無理
■必ず「第ｎ部分和の式」を確定してから，その極限を求めること

【例２】　次の無限級数の和を求めてください．
$\frac{1}{\sqrt{2}+ 1}+\frac{1}{\sqrt{3}+\sqrt{2}}+\cdots+\frac{1}{\sqrt{n+ 1}+\sqrt{n}}+\cdots$

（解答）
第ｎ部分和を求める
$\frac{1}{\sqrt{k+ 1}+\sqrt{k}}=\sqrt{k+ 1}-\sqrt{k}$
だから，第ｎ部分和は
$S_n=(\sqrt{2}-1)+(\sqrt{3}-\sqrt{2})+\cdots+(\sqrt{n+ 1}-\sqrt{n})$
$=\hspace{10}(\cancel{\sqrt{2}}-1)$

第ｎ部分和（有限数列の和）では，どの順に足したり引いたりしても結果は変わらない

$+(\cancel{\sqrt{3}}-\cancel{\sqrt{2}})$
$+(\cancel{\sqrt{4}}-\cancel{\sqrt{3}})$
$+\cdots\hspace{3}\cdots$
$+(\sqrt{n+ 1}-\cancel{\sqrt{n}})$
$=\sqrt{n+ 1}-1$
$\lim_{n\rightarrow \infty}S_n=\lim_{n\rightarrow \infty}(\sqrt{n+ 1}-1)=\infty$
したがって，この無限級数は発散する．

【問題１】　次の無限級数の収束・発散について調べ，収束するときはその和を求めなさい．（選択肢の中から正しいものを１つクリック）

(1)
$\lim_{n\rightarrow\infty}\sum_{k=1}^n\frac{1}{(2k+ 1)(2k+ 3)}$

解説やり直す

$\frac{1}{6}$ $\frac{1}{2}$ $1$ 発散する

第ｎ部分和を求める
$\frac{1}{(2k+ 1)(2k+ 3)}=\frac{1}{2}(\frac{1}{2k+ 1}-\frac{1}{2k+ 3})$
だから，第ｎ部分和は
$S_n=\hspace{10}\frac{1}{2}(\frac{1}{3}-\cancel{\frac{1}{5}})$

第ｎ部分和（有限数列の和）では，どの順に足したり引いたりしても結果は変わらない

$+\frac{1}{2}(\cancel{\frac{1}{5}}-\cancel{\frac{1}{7}})$
$+\cdots\hspace{3}\cdots$
$+\frac{1}{2}(\cancel{\frac{1}{2n+ 1}}-\frac{1}{2n+ 3})$
$=\frac{1}{2}(\frac{1}{3}-\frac{1}{2n+ 3})$
したがって
$\lim_{n\rightarrow\infty}\sum_{k=1}^n\frac{1}{(2k+ 1)(2k+ 3)}=\lim_{n\rightarrow\infty}S_n=\frac{1}{6}$ …（答）

→閉じる←

(2)
$\sum_{n=1}^{\infty}\frac{1}{\sqrt{2n+ 1}+\sqrt{2n-1}}$

解説やり直す

$\frac{1}{6}$ $\frac{1}{2}$ $1$ 発散する

第ｎ部分和を求める
$\frac{1}{\sqrt{2k+ 1}+\sqrt{2k-1}}=\frac{\sqrt{2k+ 1}-\sqrt{2k-1}}{(2k+ 1)-(2k-1)})$
$=\frac{1}{2}(\sqrt{2k+ 1}-\sqrt{2k-1})$

第ｎ部分和（有限数列の和）では，どの順に足したり引いたりしても結果は変わらない

だから，第ｎ部分和は
$S_n=\hspace{10}\frac{1}{2}(\cancel{\sqrt{3}}-1)$
$+\frac{1}{2}(\cancel{\sqrt{5}}-\cancel{\sqrt{3}})$
$+\cdots\hspace{3}\cdots$
$+\frac{1}{2}(\sqrt{2n+ 1}-\cancel{\sqrt{2n-1}})$
$=\frac{1}{2}(\sqrt{2n+ 1}-1)$
したがって，この無限級数は発散する …（答）

→閉じる←

【無限級数の性質】

【Ⅰ 無限級数が収束するための必要条件】
(1) $\sum_{n=1}^{\infty}a_n$ が収束する $\Rightarrow\lim_{n\rightarrow\infty}a_n=0$
(2) $\lim_{n\rightarrow\infty}a_n\ne 0$ $\Rightarrow\sum_{n=1}^{\infty}a_n$ は発散する

※(1)は必要条件ではあるが，十分条件ではないことに注意．すなわち $\lim_{n\rightarrow\infty}a_n=0$ だからといって，無限級数が収束するとは言えない．

【Ⅱ 収束する無限級数の和差，実数倍】
$\sum_{n=1}^{\infty}a_n=\alpha,\hspace{5}\sum_{n=1}^{\infty}b_n=\beta$ のとき

(1) $\sum_{n=1}^{\infty}(a_n+ b_n)=\alpha+\beta$
(2) $\sum_{n=1}^{\infty}(a_n-b_n)=\alpha-\beta$
(3) $\sum_{n=1}^{\infty}ka_n=k\alpha$

※　有限数列の和とは異なり，無限級数の和を求めるときに，足し方の順序を勝手に変えることはできない．
　これに対して，上記のⅡ(1)(2)(3)は，「収束する無限級数」の和差，実数倍に限って，順序の変更は「何でもあり」だということを示している．
　「収束しない無限級数」や「収束するかしないか分からない無限級数」では，そんなことはできない．

（解説）
Ⅰ(1) ←

8両連結の列車の前に，7両連結の列車を止めると

n両連結の列車の前に，n−1両連結の列車を止めると

無限級数 $\sum a_n$ の第ｎ部分和を $S_n$ とすると
$a_n=S_n-S_{n-1}$
が成り立つ．（右図参照）

第ｎ部分和が収束するとき
$\lim_{n\rightarrow\infty}S_n=S$
とおくと
$\lim_{n\rightarrow\infty}S_{n-1}=S$
も成り立つから
$\lim_{n\rightarrow\infty}a_n$
$=\lim_{n\rightarrow\infty}(S_n-S_{n-1})$
$=S-S=0$

これにより，無限級数が収束するのは，数列が０に収束する場合だけであることが証明できた．

Ⅰ(2) ←
Ⅰ(1)の対偶をとると，数列 $\{a_n\}$ が０に収束しないならば，無限級数は発散すると言える．

【例３】　次の無限級数の収束・発散を調べてください．
$\lim_{n\rightarrow\infty}\sum_{k=1}^n\frac{k}{k+ 1}$

（解答）
$\lim_{n\rightarrow\infty}\frac{k}{k+ 1}=\lim_{n\rightarrow\infty}(1-\frac{1}{k+ 1})=1\ne 0$
は０に収束しないから，元の無限級数は発散する．…（答）

【例４】　次の無限級数の収束・発散を調べてください．
$1-1+ 1-1+\cdots$

（解答）
数列の第ｎ項は $a_n=(-1)^{n+ 1}$
ア）ｎが奇数のときｎ+1は偶数だから
$\lim_{n\rightarrow\infty}a_n=\lim_{n\rightarrow\infty}(-1)^{n+ 1}=1$
イ）ｎが偶数のときｎ+1は奇数だから
$\lim_{n\rightarrow\infty}a_n=\lim_{n\rightarrow\infty}(-1)^{n+ 1}=-1$
ｎが限りなく大きくなるとき，どこまで行っても偶数と奇数が登場するから， $a_n$ は０に収束しない．
したがって，無限級数は発散する．…（答）

（別解）第ｎ部分和を使って証明する方法（このページの先頭に書いている）
第ｎ部分和は
$S_1=1$
$S_2=1-1=0$
$S_3=1-1+ 1=1$
$S_4=1-1+ 1-1=0$
だから
ア）ｎが奇数のとき
$S_n=1$
イ）ｎが偶数のとき
$S_n=0$
ｎが限りなく大きくなるとき，どこまで行っても偶数と奇数が登場するから， $S_n$ は収束しない．
したがって，無限級数は発散する．…（答）

なお
【例１】
$\frac{1}{1\cdot 2}+\frac{1}{2\cdot 3}+\frac{1}{3\cdot 4}+\cdots+\frac{1}{n(n+ 1)}+\cdots=1$
$\Big(\hspace{10}\lim_{n\rightarrow\infty}\frac{1}{n(n+ 1)}=0\hspace{10}\Big)$
【例２】
$\frac{1}{\sqrt{2}+ 1}+\frac{1}{\sqrt{3}+\sqrt{2}}+\cdots+\frac{1}{\sqrt{n+ 1}+\sqrt{n}}+\cdots$ は発散する
$\Big(\hspace{10}\lim_{n\rightarrow\infty}\frac{1}{\sqrt{n+ 1}+\sqrt{n}}=0\hspace{10}\Big)$
のように， $a_n\rightarrow 0$ であっても，無限級数が収束する場合と発散する場合があることに注意．
Ⅰ(2)は， $a_n\rightarrow \ne 0$ のときに発散することの証明に使えるが， $a_n\rightarrow 0$ のときには，無限級数が収束する場合も，発散する場合もあるので，別途その証明が必要となる．

$a_n\rightarrow 0$ の場合に，無限級数の収束・発散を判別することは，かなり難しい問題になる場合がある．

（解説）
Ⅱ(1)(2)(3) ←

$\sum_{n=1}^{\infty}a_n=\alpha,\hspace{5}\sum_{n=1}^{\infty}b_n=\beta$ のとき

(1) $\sum_{n=1}^{\infty}(a_n+ b_n)=\alpha+\beta$
(2) $\sum_{n=1}^{\infty}(a_n-b_n)=\alpha-\beta$
(3) $\sum_{n=1}^{\infty}ka_n=k\alpha$

これらの性質は，収束する数列の性質と同じなので，高校ではこれ以上詳しく証明しません．（さらに踏み込んで証明するには，ε-δ論法を使いますが，これは高校数学の範囲外です）．

ここで覚えておくべきことは，上記のように収束する無限級数については，(1)のように足し算の順序を変えて，分けて計算してもよいということ
$\sum_{n=1}^{\infty}(a_n+ b_n)=\sum_{n=1}^{\infty}a_n+\sum_{n=1}^{\infty}b_n$
(2)のように引き算の順序を変えて，分けて計算してもよい
$\sum_{n=1}^{\infty}(a_n-b_n)=\sum_{n=1}^{\infty}a_n-\sum_{n=1}^{\infty}b_n$
(3)のように実数（定数）を掛けてから足しても，足してから掛けてもよい
$\sum_{n=1}^{\infty}ka_n=k\sum_{n=1}^{\infty}a_n$
⇒ 要するに，１つずつが収束する無限級数の和差，実数倍については，計算の順序の入れ換えは「何でもあり」ということです．
⇒ これに対して，１つずつが収束するとは限らない無限級数の和差，実数倍の順序を勝手に入れ変えると，正しい変形という保証がなくなります．この場合は，原則通り「第ｎ部分和」を作って，その極限を考えるのみです．

Ⅲ【無限等比級数の和】
　無限等比級数
$a+ ar+ ar^2+ \cdots+ ar^{n-1}+\cdots$
の収束・発散一覧

	イ） $a\ne 0$	ア） $a=0$
$r\gt 1$	発散する	収束する．和は $0$
$r=1$	発散する
$-1\lt r\lt 1$	収束する．和は $\frac{a}{1-r}$
$r=-1$	発散する
$r\lt -1$	発散する

（解説）
ア） $a=0$ のとき
$0+ 0+ 0+ \cdots+ 0+\cdots=0$
となるから，無限級数は収束し，その和は０になる．
イ） $a\ne 0$ のとき
第ｎ部分和は
$S_n=a+ ar+ ar^2+ \cdots+ ar^{n-1}$

(その１) $r=1$ のとき
$S_n=a+ a+ a+ \cdots+ a=na$
$a\ne 0$ であるから，Ⅰ(2)により， $n\rightarrow\infty$ のとき発散する．

(その２) $r\ne 1$ のとき
$S_n=a+ ar+ ar^2+ \cdots+ ar^{n-1}$
は，初項 $a$ ，公比 $r$ ，項数 $n$ の等比数列の和であるから
$S_n=\frac{a(r^n-1)}{r-1}=\frac{a(1-r^n)}{1-r}$

数学Ⅱで習うときは，等比数列の和は，分母分子ともｒの次数の高い項を前にして
$S_n=\frac{a(r^n-1)}{r-1}$
とするが，この式は分母分子にそれぞれ１を掛けた次の式に等しい
$S_n=\frac{a(1-r^n)}{1-r}$
場面に応じて，使いやすい方を使う

その i) $r\gt 1$ のとき
$r^n\rightarrow\infty$ だから $S_n$ は正の無限大に発散する．
その ii) $-1\lt r\lt 1$ のとき
$r^n\rightarrow 0$ だから $S_n=\frac{a(1-r^n)}{1-r}\rightarrow\frac{a}{1-r}$
その iii) $r=-1$ のとき
$r^n$ は±1を振動して収束しないから， $S_n$ は発散する．
その iv) $r\lt -1$ のとき
$r^n$ は正負の無限大を振動して収束しないから， $S_n$ は発散する．

※ $a\ne 1$ のとき，次の違いに注意
無限等比数列
$a,\hspace{3}ar,\hspace{3}ar^2,\hspace{3}\cdots,\hspace{3}ar^{n-1},\hspace{3}\cdots\hspace{5}$
の収束条件は $-1\lt r\underline{\le}1$
無限等比級数
$a+ ar+ ar^2+ \cdots+ ar^{n-1}+\cdots$
の収束条件は $-1\lt r\lt 1$

$r=1$
のところだけが
異なる

【例５】　次の無限級数の収束・発散を調べてください．
$\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\cdots$

（解答）
第ｎ部分和
$S_n=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\cdots+\frac{1}{2^{n}}$
は，初項 $\frac{1}{2}$ ，公比 $\frac{1}{2}$ ，項数 $n$ の等比数列の和であるから

$S_n=\frac{\frac{1}{2}\{1-(\frac{1}{2})^n\}}{1-\frac{1}{2}}\rightarrow\frac{\frac{1}{2}}{1-\frac{1}{2}}=1$

【例６】　次の無限等比級数が収束するような $x$ の値の範囲とそのときの和を求めてください．
$1+(1-x)+(1-x)^2+(1-x)^3+\cdots$

（解答）
初項 $1\hspace{3}(\ne 0)$ ，公比 $1-x$ の無限等比級数であるから
$-1\lt 1-x\lt 1$
すなわち
$0\lt x\lt 2$
のとき収束する．このとき和は
$\frac{1}{1-(1-x)}=\frac{1}{x}$

【問題２】　次の無限級数級数の収束・発散について調べ，収束するときはその和を求めなさい．（選択肢の中から正しいものを１つクリック）

(1)　
$1-\frac{1}{2}+\frac{1}{4}-\frac{1}{8}+\cdots$

解説やり直す

$\frac{1}{3}$ $\frac{1}{2}$ $\frac{2}{3}$ 発散する

初項 $1\hspace{3}(\ne 0)$ ，公比 $-\frac{1}{2}\hspace{3}(\ne 1)$ の無限等比級数であるから
収束し，その和は
$\frac{1}{1-(-\frac{1}{2})}=\frac{2}{3}$ …（答）

→閉じる←

(2)　
$\sum_{n=1}^{\infty}\big(\frac{1}{2^n}-\frac{1}{3^n}\big)$

解説やり直す

$\frac{1}{6}$ $\frac{1}{3}$ $\frac{1}{2}$ 発散する

一般には，無限級数の和を求めるときに，計算の順序を勝手に変えることはできないが，それぞれが収束する無限級数については，求めた結果の差に等しいⅡ(2)
$\sum_{n=1}^{\infty}(a_n-b_n)=\sum_{n=1}^{\infty}a_n-\sum_{n=1}^{\infty}b_n$
したがって，次のように計算できる．
$\sum_{n=1}^{\infty}\frac{1}{2^n}-\sum_{n=1}^{\infty}\frac{1}{3^n}$
$=\big(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\cdots\big)-\big(\frac{1}{3}+\frac{1}{9}+\frac{1}{27}+\cdots\big)$
$=\frac{\frac{1}{2}}{1-\frac{1}{2}}-\frac{\frac{1}{3}}{1-\frac{1}{3}}=1-\frac{1}{2}=\frac{1}{2}$ …（答）

（別解）
第ｎ部分和から求めると，有限数列の和になるから，和差の順序を入れ換えても等しい．
$S_n=\sum_{k=1}^{n}\big(\frac{1}{2^k}-\frac{1}{3^k}\big)$
$=\big(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\cdots+\frac{1}{2^n}\big)-\big(\frac{1}{3}+\frac{1}{9}+\frac{1}{27}+\cdots+\frac{1}{3^n}\big)$
各々，初項 $\frac{1}{2}$ ，公比 $\frac{1}{2}$ ，項数 $n$ の等比数列の和，
および初項 $\frac{1}{3}$ ，公比 $\frac{1}{3}$ ，項数 $n$ の等比数列の和であるから
$S_n=\frac{\frac{1}{2}\big(1-(\frac{1}{2})^n\big)}{1-\frac{1}{2}}-\frac{\frac{1}{3}\big(1-(\frac{1}{3})^n\big)}{1-\frac{1}{3}}$
$\rightarrow\frac{\frac{1}{2}}{1-\frac{1}{2}}-\frac{\frac{1}{3}}{1-\frac{1}{3}}=1-\frac{1}{2}=\frac{1}{2}$
に収束する …（答）

→閉じる←

【問題３】　次の無限等比級数が収束するような $x$ の値の範囲を求めてください．（選択肢の中から正しいものを１つクリック）

(1)　
$\sum_{n=1}^{\infty}(x^2+ x)^n$

解説やり直す

$-1\lt x\lt 1$ $\frac{1-\sqrt{3}}{2}\lt x\lt\frac{1+\sqrt{3}}{2}$

$\frac{1+\sqrt{3}}{2}\lt x\lt\frac{1+\sqrt{5}}{2}$ $\frac{-1-\sqrt{5}}{2}\lt x\lt\frac{-1+\sqrt{5}}{2}$

初項 $x^2+ x$ ，公比 $x^2+ x$ の無限等比級数であるから，Ⅲにより，収束するのは
ア）初項 $x^2+ x=0$ の場合
イ）初項 $x^2+ x\ne 0$ かつ公比 $-1\lt x^2+ x\lt 1$ の場合
ア）より $x=0,\hspace{3}-1$
イ）より

$x\ne 0,\hspace{3}x\ne -1$ …(1)
$-1\lt x^2+ x\lt 1$ …(2)
(2)より

$x^2+ x+ 1\gt 0$ …(2.1)
$x^2+ x-1\lt 0$ …(2.2)
(2.1)は，判別式 $D=1-4=-3\lt 0$ によりつねに成立する．（もしくは， $x^2+ x+ 1=(x+\frac{1}{2})^2+\frac{3}{4}\gt 0$ だから，つねに成立する）
(2.2)より $\frac{-1-\sqrt{5}}{2}\lt x\lt\frac{-1+\sqrt{5}}{2}$
以上から，ア）イ）の範囲を合わせると
$\frac{-1-\sqrt{5}}{2}\lt x\lt\frac{-1+\sqrt{5}}{2}$ …（答）

→閉じる←

(2)　
$x+ x(x-1)+ x(x-1)^2+\cdots$

解説やり直す

$-2\lt x\underline{\le}0$ $-1\lt x\lt 1$

$0\lt x\lt 2$ $0\underline{\le}x\lt 2$

初項 $x$ ，公比 $x-1$ の無限等比級数であるから，Ⅲにより，収束するのは
ア）初項 $x=0$ の場合
イ）初項 $x\ne 0$ かつ公比 $-1\lt x-1\lt 1$ の場合
ア）より $x=0$
イ）より

$x\ne 0$ …(1)
$-1\lt x-1\lt 1$ …(2)
(2)より
$0\lt x\lt 2$
以上から，ア）イ）の範囲を合わせると
$0\underline{\le}x\lt 2$ …（答）

→閉じる←

【まとめの問題】　総合復習

無限級数の和を求めるには（再掲）
■いきなり無限を考えるのは無理
■「第ｎ部分和の式」を確定してから，その極限を求めること

【Ⅰ 無限級数が収束するための必要条件】（再掲）
(1) $\sum_{n=1}^{\infty}a_n$ が収束する $\Rightarrow\lim_{n\rightarrow\infty}a_n=0$
(2) $\lim_{n\rightarrow\infty}a_n\ne 0$ $\Rightarrow\sum_{n=1}^{\infty}a_n$ は発散する
※収束しないことは，簡単に示せることがある．

【問題４】　次の無限級数の収束・発散を調べ，収束するときは和を求めてください．（選択肢の中から正しいものを１つクリック）

(1)　
$1-2+ 3-4+ 5-\cdots$

解説やり直す

$+\inft$ に発散する $-\inft$ に発散する

振動する（発散する） $1$ に収束する

第ｎ部分和を $S_n$ とおくと
$S_1=1$
$S_2=1-2=-1$
$S_3=1-2+ 3=2$
$S_4=1-2+ 3-4=-2$
$S_5=1-2+ 3-4+ 5=3$
$\cdots\hspace{3}\cdots$
したがって，
ア） $n$ が奇数（ $n=2m-1$ ）のとき
$S_n=m$
イ） $n$ が偶数（ $n=2m$ ）のとき
$S_n=-m$
正負の値を交互に取りながら，絶対値の大きな値になるから，「振動する（発散する） …（答）

この問題では，数列の第ｎ項が $a_n=(-1)^{n-1}n$ となって，０に収束しないから，無限級数は収束しない（発散する）は言えるが，それだけでは「どの発散か」の区別はできない．

→閉じる←

(2)　
$(0-\frac{1}{2})+(\frac{1}{2}-\frac{2}{3})+(\frac{2}{3}-\frac{3}{4})+\cdots$

解説やり直す

$-\inft$ に発散する振動する（発散する）

$-1$ に収束する $0$ に収束する

かっこの中は先に計算しなければなりません．したがって，第ｎ項にはかっこｎ個分（分数2ｎ個）まで入ります．
第ｎ部分和を $S_n$ とおくと
$S_n=\hspace{10}(0-\cancel{\frac{1}{2}})$
$+(\cancel{\frac{1}{2}}-\cancel{\frac{2}{3}})$
$+(\cancel{\frac{2}{3}}-\cancel{\frac{3}{4}})$
$\cdots\hspace{3}\cdots$
$+(\cancel{\frac{n-1}{n}}-\frac{n}{n+ 1})$
$=0-\frac{n}{n+ 1}=-1+\frac{1}{n+ 1}\rightarrow -1$ …（答）

（参考）
もし問題が， $0-\frac{1}{2}+ \frac{1}{2}-\frac{2}{3}+ \frac{2}{3}-\frac{3}{4}+\cdots$ となっていたら，全く異なる結果になります．
≪第ｎ部分和から求める場合≫
$S_1=0,\hspace{3}S_2=-\frac{1}{2},\hspace{3}S_3=0,\hspace{3}S_4=-\frac{2}{3}$
ア）ｎが奇数のとき， $S_n=0\rightarrow 0$
イ）ｎが偶数のとき， $S_n=-\frac{n-2}{n-1}\rightarrow -1$
一致しないから，無限級数は収束しない（振動して発散）
≪数列の第ｎ項から発散を示す場合≫
$a_1=0,\hspace{3}a_2=-\frac{1}{2},\hspace{3}a_3=\frac{1}{2},\hspace{3}a_4=-\frac{2}{3}$
ア）ｎが奇数（ $n=2m-1$ ）のとき， $a_n=\frac{m-1}{m}\rightarrow 1$
イ）ｎが偶数（ $n=2m$ ）のとき， $a_n=-\frac{m}{m+ 1}\rightarrow -1$
数列が0に収束しないから，無限級数は収束しない

→閉じる←

【問題４】　次の無限級数の収束・発散を調べ，収束するときは和を求めてください．（選択肢の中から正しいものを１つクリック）

(3)　
$\sum_{n=1}^{\infty}\frac{1}{n(n+ 1)(n+ 2)}$

解説やり直す

発散する $\frac{1}{4}$ に収束する

$\frac{1}{3}$ に収束する $\frac{1}{2}$ に収束する

分母がｎの３次式=分数がｎの－３次式のものを差で表すには，（１次次数を高くして）分数がｎの－２次式=分母がｎの２次式の差にする
$\frac{1}{n(n+ 1)(n+ 2)}=\frac{1}{2}\{\frac{1}{n(n+ 1)}-\frac{1}{(n+ 1)(n+ 2)}\}$
だから，第ｎ部分和は
$S_n=\hspace{10}\frac{1}{2}\{\frac{1}{1\cdot 2}-\cancel{\frac{1}{2\cdot 3}}\}$
$+\frac{1}{2}\{\cancel{\frac{1}{2\cdot 3}}-\cancel{\frac{1}{3\cdot 4}}\}$
$\cdots\hspace{3}\cdots$
$+\frac{1}{2}\{\cancel{\frac{1}{n(n+ 1)}}-\frac{1}{(n+ 1)(n+ 2)}\}$
$=\frac{1}{2}\{\frac{1}{2}-\frac{1}{(n+ 1)(n+ 2)}\}\rightarrow\frac{1}{4}$ …（答）

→閉じる←

【問題４】　次の無限級数の収束・発散を調べ，収束するときは和を求めてください．（選択肢の中から正しいものを１つクリック）

(4)　
$\sum_{n=1}^{\infty}\frac{1}{\sqrt{3n+ 2}+\sqrt{3n-1}}$

解説やり直す

発散する $\frac{1}{4}$ に収束する

$\frac{1}{3}$ に収束する $\frac{1}{2}$ に収束する

分母を有理化すると分子が差になる
$\frac{1}{\sqrt{3n+ 2}+\sqrt{3n-1}}=\frac{\sqrt{3n+ 2}-\sqrt{3n-1}}{(3n+ 2)-(3n-1)}$
$=\frac{1}{3}\{\sqrt{3n+ 2}-\sqrt{3n-1}\}$
だから，第ｎ部分和は
$S_n=\hspace{10}\frac{1}{3}\{\cancel{\sqrt{5}}-\sqrt{2}\}$
$+\frac{1}{3}\{\cancel{\sqrt{8}}-\cancel{\sqrt{5}}\}$
$\cdots\hspace{3}\cdots$
$+\frac{1}{3}\{\sqrt{3n+ 2}-\cancel{\sqrt{3n-1}}\}$
$=\frac{1}{3}\{\sqrt{3n+ 2}-\sqrt{2}\}\rightarrow\infty$ …（答）
※同様の問題は前にも出てますが，数列の一般項が $a_n\rightarrow 0$ であっても，無限級数が発散する場合の例になっています．

→閉じる←

Ⅲ【無限等比級数の和】（再掲）
　無限等比級数
$a+ ar+ ar^2+ \cdots+ ar^{n-1}+\cdots$
の収束・発散

	イ） $a\ne 0$	ア） $a=0$
$r\gt 1$	発散する	収束する．和は $0$
$r=1$	発散する
$-1\lt r\lt 1$	収束する．和は $\frac{a}{1-r}$
$r=-1$	発散する
$r\lt -1$	発散する

【問題５】　次の無限等比級数の収束・発散を調べてください．（選択肢の中から正しいものを１つクリック）

(1)　
$\sum_{n=1}^{\infty}\big(\frac{x}{x^2+ 1}\big)^n$

解説やり直す

$\frac{1-\sqrt{3}}{2}\lt x\lt\frac{1+\sqrt{3}}{2}$ のとき収束する

$\frac{1-\sqrt{5}}{2}\lt x\lt\frac{1+\sqrt{5}}{2}$ のとき収束する

つねに収束するつねに発散する

初項 $\frac{x}{x^2+ 1}$ ，公比 $\frac{x}{x^2+ 1}$ の無限等比級数であるから，Ⅲにより，収束するのは
ア）初項 $\frac{x}{x^2+ 1}=0$ の場合
イ）初項 $\frac{x}{x^2+ 1}\ne 0$ かつ公比 $-1\lt \frac{x}{x^2+ 1}\lt 1$ の場合
ア）より $x=0$
イ）より

$x\ne 0$ …(1)
$-1\lt \frac{x}{x^2+ 1}\lt 1$ …(2)
(2)より（分母 $x^2+ 1(\gt 0)$ を払うと）

$x^2-x+ 1\gt 0$ …(2.1)
$x^2+ x+ 1\gt 0$ …(2.2)
(2.1)(2.2)はいずれも判別式＜０の絶対不等式で，つねに成り立つ．
以上から，ア）イ）の範囲を合わせると， $x$ は任意の実数
したがって，無限等比級数はつねに収束する …（答）

→閉じる←

【問題５】　次の無限等比級数の和を求めてください．（選択肢の中から正しいものを１つクリック）

(2)　
$\sum_{n=1}^{\infty}\frac{2^n+ 3^n}{5^n}$

解説やり直す

$1$ $\frac{13}{6}$ $\frac{19}{6}$ 発散する

$\sum_{n=1}^{\infty}(\frac{2}{5})^n,\hspace{3}\sum_{n=1}^{\infty}(\frac{3}{5})^n$ が各々収束するから，各項の和の極限も収束する．
$\sum_{n=1}^{\infty}(\frac{2}{5})^n=\frac{\frac{2}{5}}{1-\frac{2}{5}}=\frac{2}{3}$
$\sum_{n=1}^{\infty}(\frac{3}{5})^n=\frac{\frac{3}{5}}{1-\frac{3}{5}}=\frac{3}{2}$
だから
$\frac{2}{3}+\frac{3}{2}=\frac{13}{6}$ …（答）

→閉じる←

【Ⅱ 収束する無限級数の和差，実数倍】
$\sum_{n=1}^{\infty}a_n=\alpha,\hspace{5}\sum_{n=1}^{\infty}b_n=\beta$ のとき

(1) $\sum_{n=1}^{\infty}(a_n+ b_n)=\alpha+\beta$
(2) $\sum_{n=1}^{\infty}(a_n-b_n)=\alpha-\beta$
(3) $\sum_{n=1}^{\infty}ka_n=k\alpha$

【問題６】　次の無限級数の収束・発散について正しいものを選んでください．

(1)　
$\sum_{n=1}^{\infty}(a_n+ b_n),\hspace{5}\sum_{n=1}^{\infty}(a_n-b_n)$ がいずれも収束するとき， $\sum_{n=1}^{\infty}a_n,\hspace{5}\sum_{n=1}^{\infty}b_n$ は

解説やり直す

つねに収束する

収束するときも発散するときもある

つねに発散する

第ｎ部分和をそれぞれ
$\sum_{k=1}^{n}(a_k+ b_k)=S_n,\hspace{3}\sum_{k=1}^{n}(a_k-b_k)=T_n$
とおくと
$S_n,\hspace{3}T_n$ は収束するから，それらの和差，実数倍
$\sum_{k=1}^{n}a_n=\frac{S_n+ T_n}{2}$
も収束する．したがって
$\lim_{n\rightarrow\infty}\sum_{k=1}^{n}a_n=\lim_{n\rightarrow\infty}\frac{S_n+ T_n}{2}$
$\lim_{n\rightarrow\infty}\sum_{k=1}^{n}b_n=\lim_{n\rightarrow\infty}\frac{S_n-T_n}{2}$
は，つねに収束する． …（答）

→閉じる←

(2)　
$\sum_{n=1}^{\infty}(a_n+ b_n)=\infty,\hspace{5}\sum_{n=1}^{\infty}(a_n-b_n)=0$ のとき， $\sum_{n=1}^{\infty}a_n=\sum_{n=1}^{\infty}b_n=\infty$ は

解説やり直す

つねに成立する

つねには成立しない

絶対成立しない

第ｎ部分和をそれぞれ
$\sum_{k=1}^{n}(a_k+ b_k)=S_n,\hspace{3}\sum_{k=1}^{n}(a_k-b_k)=T_n$
とおくと
$S_n\rightarrow \infty,\hspace{3}T_n\rightarrow 0$ だから
$\lim_{n\rightarrow\infty}\sum_{k=1}^{n}a_n=\lim_{n\rightarrow\infty}\frac{S_n+ T_n}{2}=\infty$
$\lim_{n\rightarrow\infty}\sum_{k=1}^{n}b_n=\lim_{n\rightarrow\infty}\frac{S_n-T_n}{2}=\infty$
が成立する． …（答）

→閉じる←

【 $a_n\rightarrow 0$ のとき $S_n$ 収束？の微妙な問題】
Ⅰ(1)(2)により，
$a_n\rightarrow \ne 0$ のときは， $S_n$ は発散
これに対して，
$a_n\rightarrow 0$ のときは， $S_n$ は収束する場合も発散する場合もあります．（【例1】【例2】参照）

第ｎ項がｎの累乗となっている級数については
ア） $\sum_{n=1}^{\infty}\frac{1}{n}=\infty$ （収束しない）
イ） $0\lt k\lt 1$ のとき
$\sum_{n=1}^{\infty}\frac{1}{n^k}=\infty$ （収束しない）

【例】
$1+\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{3}}+\cdots=\infty$
$1+\frac{1}{2^{0.9}}+\frac{1}{3^{0.9}}+\cdots=\infty$

ウ） $k\gt 1$ のとき
$\sum_{n=1}^{\infty}\frac{1}{n^k}$ は収束する

【例】
$1+\frac{1}{2^2}+\frac{1}{3^2}+\cdots$ 収束する
$1+\frac{1}{2\sqrt{2}}+\frac{1}{3\sqrt{3}}+\cdots$ 収束する

（解説）
1) $1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\cdots$
のように正負の項が交互に登場するときは，増減が相殺されて収束する可能性がありますが
$1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\cdots$
のように正の項ばかりであるときは，増える一方なので無限大に発散するかのように見えますが，そうとは限りません．
2)　たとえば，今までに登場した例で
$\frac{1}{2}+(\frac{1}{2})^2+(\frac{1}{2})^3+\cdots=\frac{\frac{1}{2}}{1-\frac{1}{2}}=1$
$\frac{1}{1\cdot 2}+\frac{1}{2\cdot 3}+\frac{1}{3\cdot 4}+\cdots+\frac{1}{n(n+ 1)}+\cdots=1$
では数列の第ｎ項 $(\frac{1}{2})^n,\hspace{3}\frac{1}{n(n+ 1)}$ が急速に０に近付くので，無限回足していっても，和は無限大になりません．
3)　そこで，正の項ばかりを足していく級数において， $a_n\rightarrow 0$ がどの位の速さで０に近付けば無限級数が収束するのか，どの位なら収束しないのかについて調べてみます．

ア）の証明
　以下の解説は，数学Ⅲの定積分の知識を必要とします．

　図のように， $y=\frac{1}{x}$ のグラフと柱状グラフを重ねて描くと，曲線の下にできる図形の面積よりも柱状図形の面積の方が大きくなります．
$\int_1^2\frac{1}{x}dx\lt 1$
$\int_2^3\frac{1}{x}dx\lt\frac{1}{2}$
$\int_3^4\frac{1}{x}dx\lt\frac{1}{3}\hspace{10}\cdots\hspace{2}\cdots$
$\int_n^{n+ 1}\frac{1}{x}dx\lt\frac{1}{n}$
辺々加えるたとき，左辺は1からn+1までの定積分でつながるから
$\int_1^{n+ 1}\frac{1}{x}dx\lt 1+\frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{n}$
$\left[\log x\right]_1^{n+ 1}\lt 1+\frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{n}$
$\log(n+ 1)\lt 1+\frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{n}$
ここで $n\rightarrow\infty$ の極限をとると
$\lim_{n\rightarrow\infty}\log(n+ 1)=\infty$
だから
$1+\frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{n}\rightarrow\infty$

【追い出しの原理】
$a_n\underline{\le}b_n$ かつ $\sum_{n=1}^{\infty}a_n=\infty$
ならば $\sum_{n=1}^{\infty}b_n=\infty$ がいえる

※ $a_n=\frac{1}{n}$ の程度で $a_n\rightarrow 0$ となるとき，無限級数は発散するということが示された．

イ）の証明
ア）を使えばイ）は簡単に証明できます．
$0\lt k\lt 1$ のとき

分母が小さいと分数は大きくなる

$(0\lt )n^k\lt n^1$
だから
$\frac{1}{n}\lt \frac{1}{n^k}$
したがって
$\sum_{n=1}^{\infty}\frac{1}{n}\lt \sum_{n=1}^{\infty}\frac{1}{n^k}$
ここでア）により
$\sum_{n=1}^{\infty}\frac{1}{n}=\infty$
だから
$\sum_{n=1}^{\infty}\frac{1}{n^k}=\infty$

個別のｋの値に対しては，上記のような定積分を用いなくても，数列の知識だけで証明できるものがある．
【例】
$k=\frac{1}{2}$ のとき， $1+\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{3}}+\cdots=\infty$ は次の方法でも証明できます．（自分よりも小さな級数が無限大になることを示して，追い出し論法を使う）
【例２】で登場したもの
$\frac{1}{\sqrt{n+ 1}+\sqrt{n}}\lt\frac{1}{\sqrt{n}}$
だから
$\sqrt{n+ 1}-\sqrt{n}\lt\frac{1}{\sqrt{n}}$
$\sum_{k=1}^{n}\big(\sqrt{k+ 1}-\sqrt{k}\big)\lt\sum_{k=1}^{n}\frac{1}{\sqrt{k}}=S_n$
$\sqrt{n+ 1}-1\lt S_n$
左辺は無限大に発散するから，右辺も無限大に発散する．

ウ）の証明
ウ）を高校数学で証明するのは難しい．（リーマンのζ(ゼータ)関数と呼ばれる）
次の式も高校数学では証明できないが，「ほんとに収束するんだ！」と眺めるだけでよい．
$1+\frac{1}{2^2}+\frac{1}{3^2}+\cdots=\frac{\pi^2}{6}$
$1+\frac{1}{2^4}+\frac{1}{3^4}+\cdots=\frac{\pi^4}{90}$

←メニューに戻る