|
���Z�`��w��b�̐��w�p��.����.��
�Ⴑ�̃y�[�W���̖ڎ���…�N���b�N�ŃW�����v �P�D���̋Ɍ� �Ɍ��l�̋��ߕ� �����C���U�C�Ɍ��l�C�Ɍ��Ȃǂ̗p��̐��� �E���Ɍ��ƍ����Ɍ� �L���ł��邪�U�����Ċm�肵�Ȃ��� �����U���Ŋm�肵�Ȃ��� �U�����邪��������� ���Ɠ� 1. �Ɍ��l�����l�i��������l�j�ɂȂ���� 2. ���ꁨ�O�C���ꁨ���̌` 3. �s��`�̋Ɍ� �s��`�ł͂Ȃ����� �O���O�`�̕s��` �������`�̕s��` ��−���`�̕s��` �߂Â����ŕ����čl������� �Q�D�Q�ϐ����̋Ɍ��i��w�����̋��ށj �ɍ��W �Q�ϐ����̋Ɍ�(����) ���Ɠ� �Q�ϐ����̋Ɍ� |
|
�y�Ɍ��l�̋��ߕ��z�i�v��F���Z���w�V�܂ł͈̔́j
(1) ���ꂪ�O�ɂȂ�Ȃǂ̉����������Ȃ����i�ȒP�ȘA�����j�ł́C�Ɍ��l�̑���ɁC���l�i�P�ɒl�����������́j�ő�p���Ă悢�D
��
• • • • |
|
�y�����C���U�C�Ɍ��l�C�Ɍ��Ȃǂ̗p��̐����z
�p��
�@�u���w����v�̐e�w��Ƃ��Ắu���w�v�ɂ͐F�X�Ȏ�������āC�u�������_�v�̂悤�Ȃ��̂��Ɍ��Ɋ܂߂�ƕ֗��ȉ��p���L�����ė���̂�������܂���D�����ł́C���_���猾���C�u������Ƃ����͓̂���̒l�ł͂Ȃ��v�Ɛ�������ƁC��L�̕\���[���ł��܂��D �@���Ȃ킿�C������́u�Ɍ��v�ł͂��邪�u�Ɍ��l�ł͂Ȃ��v�Ɖ������Ă����ƁC��L�̕\�̂����܂��ȕ������N���A�[�ł���D ��
(1)• �܂��� • • �܂��� • ���Z�Łu�����I�ɗ�������v�Ƃ́C���̋߂Â�������s����l����Ƃ������ƁD
• �܂��� • ���Z�Łu�����I�ɗ�������v�Ƃ́C���̋߂Â�������s����l����Ƃ������ƁD
(A) ���̋Ɍ��l�����߂�D
• �Ɍ��l�Ȃ�…�i���j (B) ���̋Ɍ������߂�D (C) ==(B)�Ɠ����ƍl���Ă悢== �܂��� •
��L��(A)(B)(C)�Ɠ��l
|
|
�@�� ��
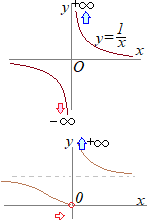 (3)
(3)(3) �p��
�@��ʂɁC
�ŕ\���D �@���ɁC �ŕ\���D �ŕ\���D �@���ɁC �ŕ\���D �@��ʂɁC �E���Ɍ��i�E������̋Ɍ��j �����Ɍ��i��������̋Ɍ��j �������Ƃ����݂��āC���C����炪��v���邱�Ƃ��Ɍ������݂��邽�߂̏����ƂȂ�D �d�v
���u���E�̂ǂ��炩����̋Ɍ������݂��Ȃ��ꍇ�v��u���E�̋Ɍ�����v���Ȃ��ꍇ�v�́C�Ɍ��Ȃ��Ƃ���D ��
(3)• �܂��� • �@ �E���Ɍ��ƍ����Ɍ�����v���Ȃ�����Ɍ��͂Ȃ��D �܂��� �E���Ɍ��ƍ����Ɍ�����v���Ȃ�����Ɍ��͂Ȃ��D ���Z�Łu�����I�ɗ�������v�Ƃ́C���̋߂Â�������s����l����Ƃ������ƁD
|
|
�@��ʂɁC
�L���ł��邪�U�����Ċm�肵�Ȃ���
(1)  
������̋Ɍ��ŁC�U�����Ď������Ȃ��ၡ
�@���̃O���t�́C���� 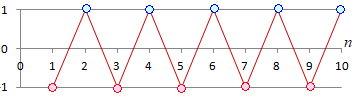
����L�̊��̋Ɍ�
 �A�j �ԊۂŎ����� �C�j �ۂŎ����� ���̂悤�ɁC �ƂȂ��āC����ɕʂ̒l�ɂȂ�D |
|
�����U���Ŋm�肵�Ȃ���
(2) 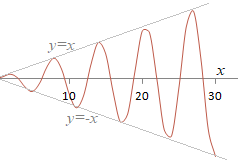 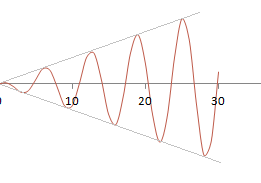
�U�����邪���������
�@�������C���̊���(1) 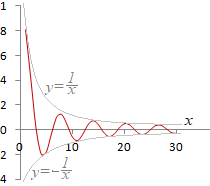 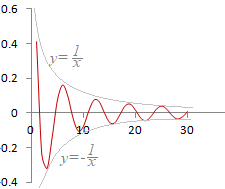
�@�M�҂̐o���Ŏv���o���ƁC���퐶���ł����̌�����ɂ́C�싅�̋���30�p���炢�̍��������Ɍ������ă��P�b�g�ʼn����t���čs���Ƃ悢�D�J�^�J�^�C�M���[���Ƃ����������āC�U�����Ȃ���~�܂�D
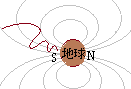 �@�n�����x���̑傫�Șb�ł́C�I�[�������k�ɁC��ɒn�������ɏo�鎖�ƊW������D���Ȃ킿�C�n������芪�����͐��͎��ɕt�߂ł͏W�܂��ĔZ���Ȃ��Ă���C���z������ł����d�q�͎��͐��ɕ����߂��ďW�܂��Ă��܂��D���ꂪ����D
�@�n�����x���̑傫�Șb�ł́C�I�[�������k�ɁC��ɒn�������ɏo�鎖�ƊW������D���Ȃ킿�C�n������芪�����͐��͎��ɕt�߂ł͏W�܂��ĔZ���Ȃ��Ă���C���z������ł����d�q�͎��͐��ɕ����߂��ďW�܂��Ă��܂��D���ꂪ����D
(2) �@���̊��ł́C�U���� 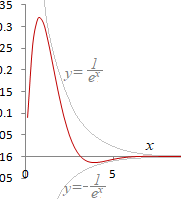 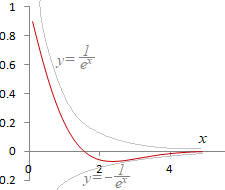
(1)��(2)�̗�ŁC��
|
|
���Ɠ�
1. �Ɍ��l�����l�i��������l�j�ɂȂ����
�@�����̊��́C��ŏK���u�A���v�Ƃ��������������āC�Ɍ��l�Ɗ��l���������D
�@���ꂪ�O�ɂȂ�Ȃǂ́u���₵���v���Ƃ��Ȃ���C�Ɍ��l�����߂����ɁC�l�������Ċ��l����悢�D •�Ɍ��l
�y���1�z
�@���̋Ɍ��l�����߂Ă��������D (1) (2) (3)
���̖��̂悤�ɁC���ꂪ0�ɂȂ�Ȃǂ́u���₵���v���Ƃ��Ȃ��C
�i�j(1) (2) (3) |
|
2. ����→�O�C����→���̌`
�@���̌`�̋Ɍ����ԈႤ���k���ȊO�ɑ����D��̓I�Ȑ��l���g���āC���̕\���C���[�W�ł���悤�ɂ��Ă������Ƃ��d�v�ł��D
�@�P�Ɂu�Ɍ��Ȃ��v�ƌ����Ă��C�Ȃ��͗l�X�Ȃ̂ŁC
�Ɠ�����D
�y���2�z
�i�j�@���̋Ɍ������߂Ă��������D (1) (2) (3) (4) (1) ����→+0�C���q→1������
�����̃y�[�W�̏��߂̕��ŗp��̐������s�����悤�ɁC���̖��̓����͂ŏ����Ƃ�,�u�Ɍ��͐��̖�����ł���v�ƂȂ�D
(2)�i��肪�Ɍ������߂Ă��������ƂȂ��Ă��邩��D���ꂪ�Ɍ��l�����߂Ă��������ƂȂ��Ă���ꍇ�́C�u�Ɍ��l�͑��݂��Ȃ��v�Ɠ����邱�ƂɂȂ�…����Șb�ɂ����Ⴒ���Ⴑ�����搶�͌������\�D��̓��Ă̂悤�Ɂ��ƊȌ��ɏ����̂��D�����[.�j ����→±0�C���q→−1������ (3) ����→������C���q=�L�������� (4) |
|
3. �s��`�̋Ɍ�
�@�s��`�̋Ɍ��Ƃ́C�u���̌������v��������s��`�ɂȂ��Ă��āC���̂܂܂̌`�ł͋Ɍ������߂��Ȃ����̂ł��D
�Ⴆ�C • • •
���q��0�������Ƃ�
(����)�{(����)�C(����)�~(����)�̂悤�ɑ傫��������̓��m��0�~0�̂悤�Ȃ��͕̂s��`�̋Ɍ��ł͂Ȃ��C�������������Ō��_��������D• |
|
** �s��`�ł͂Ȃ����� **
�y���3�z
�i�j�@���̋Ɍ������߂Ă��������D (1) (2) (1) ����́C�s��`�̋Ɍ��ł͂Ȃ��D (2) ����́C�s��`�̋Ɍ��ł͂Ȃ��D |
|
** �O���O�`�̕s��` **
�y���4�z
�i�j�@���̋Ɍ������߂Ă��������D (1) (2) 0
0
�u�v�ɂ���āC
���̕ό`�́C������s��`�̋Ɍ����������邤���ŁC�K���g�ɂ��Ȃ���Ȃ�Ȃ���{�ł��D
����ƕ��q���O�ɂȂ錴������菜���܂��D ���̂Ƃ� (2) �@���̂܂� �@ |
|
** ��÷���`�̕s��` **
�y���5�z
�@���̋Ɍ������߂Ă��������D (1) (2) (3) (*4) ����→���Ȃ�Ώ������Ȃ�C���q→���Ȃ�Α傫���Ȃ�̂ŁC�ǂ���̖����������̂�������t���܂��D ���̂悤�ȕ����^�ł́u����ƕ��q�̊e�X���ő區�ł�����v�Ƃ����ό`���L���ł��D (2) (3) (*4) �w������ΐ����Ƒ������̔�r�́C�����܂ł̏����I�Ȍv�Z�ł͂ł��܂���D���s�^���̒藝�Ȃǂ��g���Ǝ��̌��ʂ������܂��D�i��ŏq�ׂ�j |
|
** ��−���`�̕s��` **
�y���6�z
�@���̋Ɍ������߂Ă��������D (1) (2) (3)
�ő區�ł�����
(1)(2)
�����v�Z�ł́u���q�̗L�����v���L���Ȃ��Ƃ�����
(3) |
|
** �߂Â����ŕ����čl���� **
�y���7�z
(1)�@���̋Ɍ������߂Ă��������D (1) (2) (3) (4) (5) (6) �����Ɍ��ƉE���Ɍ�����v���Ȃ�����C�Ɍ��Ȃ�…�i���j (2) �����Ɍ��ƉE���Ɍ�����v���Ȃ�����C�Ɍ��Ȃ�…�i���j (3) (4) �Ɍ��Ȃ�…�i���j (5) (6) (5)�Ɠ��l�ɂ��� |
��Q�D�Q�ϐ����̋Ɍ����p��
�@�Q�ϐ���
�܂��� �ŕ\���D �d�v
�@�P�ϐ����̂Ƃ��ɁC �@�P�ϐ��̏ꍇ�C�߂Â����̈Ⴂ�Ƃ��āC�E������̋Ɍ��ƍ�������̋Ɍ����l�����C����炪�����Ƃ����݂��āC��v���邱�Ƃ��Ɍ��l�̑��ݏ����ł������D
�@�P�ϐ��̏ꍇ�C�߂Â����̈Ⴂ�Ƃ��āC�E������̋Ɍ��ƍ�������̋Ɍ����l�����C����炪�����Ƃ����݂��āC��v���邱�Ƃ��Ɍ��l�̑��ݏ����ł������D�@���E�̋Ɍ�����v����ꍇ�́C�U�����Ȃ���߂Â��ꍇ�����̒l�ƈ�v���邩��C�ǂ�ȋ߂Â��������Ă����̒l�ɋߕt���ƌ�����D 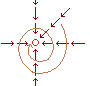 �@�Q�ϐ��̏ꍇ�Cx���ɕ��s�Ȓ����ɉ����ċ߂Â��ꍇ�C�����ɕ��s�Ȓ����ɉ����ċ߂Â��ꍇ�C���������̒����ɉ����ċ߂Â��ꍇ�C������ɉ��Ȃ���߂Â��ꍇ�ȂǁC�l�X�ȋ߂Â��������蓾�邪�C�u�߂Â��Ƃ́C������0�ɋ߂Â����Ɓv�Ƃ���C���ׂĂ̋߂Â�����s�������Ƃ��ł���D
�@�Q�ϐ��̏ꍇ�Cx���ɕ��s�Ȓ����ɉ����ċ߂Â��ꍇ�C�����ɕ��s�Ȓ����ɉ����ċ߂Â��ꍇ�C���������̒����ɉ����ċ߂Â��ꍇ�C������ɉ��Ȃ���߂Â��ꍇ�ȂǁC�l�X�ȋ߂Â��������蓾�邪�C�u�߂Â��Ƃ́C������0�ɋ߂Â����Ɓv�Ƃ���C���ׂĂ̋߂Â�����s�������Ƃ��ł���D
�@���Ȃ킿�C�Q�_ �@�Q�ϐ��̏ꍇ�C�Q�_ �ɍ��W
�@���ʏ�̓_��\�����߂ɁC���_O�Œ�������Q�����i�����Ƃ����j���g���č��W
�@����ɑ��āC���_O���ɂƂ��āC�ɂ���_ �@�ʏ�C 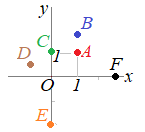 �y��z
�y��z�@�����͒������W�C���͋ɍ��W�Ƃ��āC�e�X�E�}�̓_��\���D 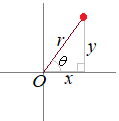 �@�������W���ɍ��W�ɒ����ɂ́C���̊W����p����D
�@�������W���ɍ��W�ɒ����ɂ́C���̊W����p����D |
|
�Q�ϐ����̋Ɍ�(����)
�y��z
(1) �ɍ��W�ŕ\�����@���̋Ɍ������߂Ă��������D (1) (2) (3) (4) (2) �ɍ��W�ŕ\���� �i
(3) �ɍ��W�ŕ\����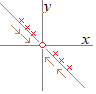 �Ɍ����Ȃ����Ƃ̏ؖ��͊ȒP�F�Ɍ������邽�߂ɂ́u�ǂ�ȋ߂Â��������Ă����̒l�ɋߕt���v���Ƃ�����������C����߂Â���������Βl����܂�Ȃ����Ƃ������Ɍ����Ȃ��ƌ�����D
�Ɍ����Ȃ����Ƃ̏ؖ��͊ȒP�F�Ɍ������邽�߂ɂ́u�ǂ�ȋ߂Â��������Ă����̒l�ɋߕt���v���Ƃ�����������C����߂Â���������Βl����܂�Ȃ����Ƃ������Ɍ����Ȃ��ƌ�����D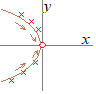 �Ɍ����Ȃ����Ƃ̏ؖ��͊ȒP�F�Ɍ������邽�߂ɂ́u�ǂ�ȋ߂Â��������Ă����̒l�ɋߕt���v���Ƃ�����������C����߂Â���������Βl����܂�Ȃ����Ƃ������Ɍ����Ȃ��ƌ�����D
�Ɍ����Ȃ����Ƃ̏ؖ��͊ȒP�F�Ɍ������邽�߂ɂ́u�ǂ�ȋ߂Â��������Ă����̒l�ɋߕt���v���Ƃ�����������C����߂Â���������Βl����܂�Ȃ����Ƃ������Ɍ����Ȃ��ƌ�����D |
|
�y���8�z
(1) �ɍ��W�ŕ\�����@���̋Ɍ������߂Ă��������D (1) (2) (3) (4) �i
(2) �ɍ��W�ŕ\����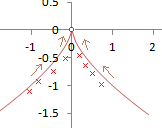 �Ɍ����Ȃ����Ƃ̏ؖ��͊ȒP�F�Ɍ������邽�߂ɂ́u�ǂ�ȋ߂Â��������Ă����̒l�ɋߕt���v���Ƃ�����������C����߂Â���������Βl����܂�Ȃ����Ƃ������Ɍ����Ȃ��ƌ�����D
�Ɍ����Ȃ����Ƃ̏ؖ��͊ȒP�F�Ɍ������邽�߂ɂ́u�ǂ�ȋ߂Â��������Ă����̒l�ɋߕt���v���Ƃ�����������C����߂Â���������Βl����܂�Ȃ����Ƃ������Ɍ����Ȃ��ƌ�����D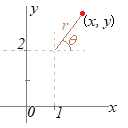 (3) �������W�ł̓_(1, 2)���ɂƂ��C�����̐��̌������n���Ƃ���ɍ��W������
(3) �������W�ł̓_(1, 2)���ɂƂ��C�����̐��̌������n���Ƃ���ɍ��W�������Ƃ����D �i
(4) �������W�ł̓_(0, −1)���ɂƂ��C�����̐��̌������n���Ƃ���ɍ��W�������Ƃ����D ���q→�L���C����→0������Ɍ��Ȃ� |