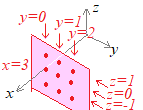
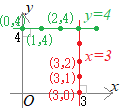
 ����3������Ԃɖ߂�ƁC�Ⴆ��x����̓_(3, 0, 0)��ʂ�Cx���ɐ����iyz���ʂɕ��s�j�ȕ��ʏ�̓_�̍��W��
����3������Ԃɖ߂�ƁC�Ⴆ��x����̓_(3, 0, 0)��ʂ�Cx���ɐ����iyz���ʂɕ��s�j�ȕ��ʏ�̓_�̍��W��
(3, 0, 0), (3, 1, 0), (3, 2, 0), ...
(3, 0, 1), (3, 1, 1), (3, 2, 1), ...
 x=3
x=3
y, z�̒l�͉��ł��悢�iy, z�̒l�ɂ͐������Ȃ��j
�����Ă��܂��D�u�����̂Ȃ����̂͏����Ȃ����悢�D�����Ȃ��D�v�̂ŁC���̕��ʂ̕�������x=3�ɂȂ�܂��D
���l�ɂ��āC�Ⴆ��y����̓_(0, 4, 0)��ʂ�Cy���ɐ����iyz���ʂɕ��s�j�ȕ��ʏ�̕�������y=4�ɂȂ�܂��D
�܂��Cz����̓_(0, 0, 5)��ʂ�Cz���ɐ����ixy���ʂɕ��s�j�ȕ��ʏ�̕�������z=5�ɂȂ�܂��D
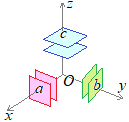
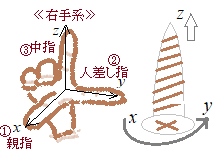
�@�����W���ɁC�u�������h���Ă���v�Ƃ��̎��̍��W�������悢�ˁI
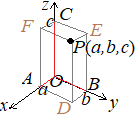
�y���W���ʂɕ��s�ȕ��ʂ̕�����2�z
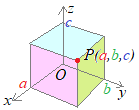
�_ P(a, b, c)��ʂ�C
yz���ʂɕ��s�ȕ��ʂ̕�������
x=a…(1)
zx���ʂɕ��s�ȕ��ʂ̕�������
y=b…(2)
xy���ʂɕ��s�ȕ��ʂ̕�������
z=c…(3)
�@�_P(a, b, c)��ʂ�Cyz���ʁCzx���ʁCxy���ʂɕ��s�ȕ��ʂ́C���W���Ɗe�X�_(a, 0, 0), (0, b, 0), (0, 0, c)�Ō���邩��C�y���W���ʂɕ��s�ȕ��ʂ̕�����1�z�ŏq�ׂ��������g����D
|
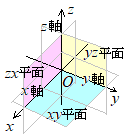
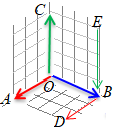
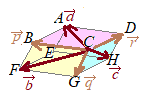
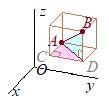 �@�E�}�̂悤��A,B��Ίp���Ƃ��钼���̂�`���ƁC�s���N�F�̎O�p�`��
�@�E�}�̂悤��A,B��Ίp���Ƃ��钼���̂�`���ƁC�s���N�F�̎O�p�`�� �@��L�̂悤�ɏ����Ƃ܂����̂́C
�@��L�̂悤�ɏ����Ƃ܂����̂́C
 �@
�@ �@���w�Z�ŏK�����悤�ɁC���ʏ��
�@���w�Z�ŏK�����悤�ɁC���ʏ�� ����3������Ԃɖ߂�ƁC�Ⴆ��
����3������Ԃɖ߂�ƁC�Ⴆ�� �_
�_ �E�}�̗�ł́C
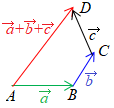
�E�}�̗�ł́C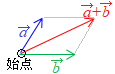 (1) �Q�̃x�N�g���́u�n�_�����낦�ĕ`���v�ƁC���s�l�ӌ`�̑Ίp���������̘a��\���D
(1) �Q�̃x�N�g���́u�n�_�����낦�ĕ`���v�ƁC���s�l�ӌ`�̑Ίp���������̘a��\���D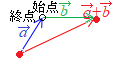 (2)
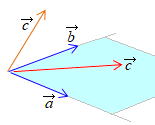
(2)  ����ʂɁC(2)�̍l�����̕���3�ȏ�̃x�N�g���̘a����x�ɕ`����_���C�L�����ƍl������D
����ʂɁC(2)�̍l�����̕���3�ȏ�̃x�N�g���̘a����x�ɕ`����_���C�L�����ƍl������D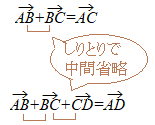
 �@1���]���ł���Ƃ��C
�@1���]���ł���Ƃ��C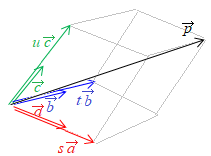
 �y��4�z
�y��4�z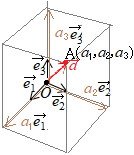
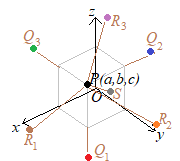
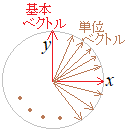 �@�P�ʃx�N�g���i�傫�����P�̃x�N�g���j�͖����ɂ��邪�C��{�x�N�g���͂R�����D
�@�P�ʃx�N�g���i�傫�����P�̃x�N�g���j�͖����ɂ��邪�C��{�x�N�g���͂R�����D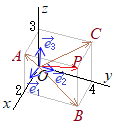 ��{�x�N�g���𐬕��\���ɂ���ƁC�e�X
��{�x�N�g���𐬕��\���ɂ���ƁC�e�X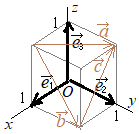 �y��5�z
�y��5�z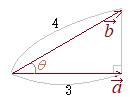 �@�Ⴆ�C�E�}�ɂ�����
�@�Ⴆ�C�E�}�ɂ�����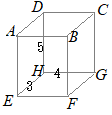 (1)
(1)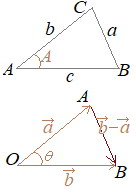 �@���ȏ��ł́C�E�}�̎O�p�`
�@���ȏ��ł́C�E�}�̎O�p�`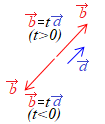 (1)
(1)