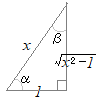|
高校〜大学基礎の数学用語.公式.例
1. 逆三角関数  の定義  のグラフは次の図のようになり,異なるxの値に同じyの値が対応する. のグラフは次の図のようになり,異なるxの値に同じyの値が対応する.
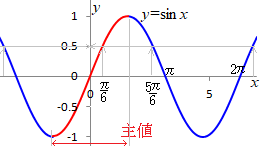
• 例えば, だから だから
 となるxの値は多数ある. となるxの値は多数ある.
• 一般に,xの範囲を限定せずに の逆関数 の逆関数 を定義すると,1つのyの値に対して多数の(無限個の)xの値が対応する「多価関数(無限多価関数)」になる. を定義すると,1つのyの値に対して多数の(無限個の)xの値が対応する「多価関数(無限多価関数)」になる.
• そこで, の逆関数の値がただ1通りに定まるように,通常,主値(principal value)と呼ばれる の逆関数の値がただ1通りに定まるように,通常,主値(principal value)と呼ばれる の区間に制限して,逆三角関数を考える.すなわち, の区間に制限して,逆三角関数を考える.すなわち,
)
)
この区間は単調増加関数で,xとyが1対1に対応するから,逆向きの対応がただ1通りに定まる.
独立変数をxで表し,従属変数をyで表す習慣に従って,文字を入れ換えて書くと
)
• なお,このように逆三角関数を定義するにあたって,主値 の区間に制限していることを示すために, の区間に制限していることを示すために, のように先頭を大文字で表すこともある.その他, のように先頭を大文字で表すこともある.その他, という記号もよく使われる. という記号もよく使われる.
以下においては,特に断りがなくても,逆三角関数 は主値を表すものとする. は主値を表すものとする.
|
定義
なお,  という記号は,「逆の」という意味を表す専用の記号として使用しており,負の指数の  という意味ではないことに注意.  や  なども定義していない
例
なお,  のような値は筆算では求められない.これは,  を満たすxの値が筆算では求められないという事情と同じである.
(逆)三角関数表またはコンピュータを使えば,小数の近似値で求められる.Excelでは ACOS( )という関数を使う.[arccosの略]
|
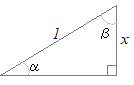 ≪
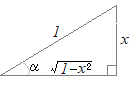
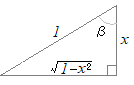
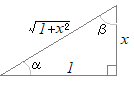
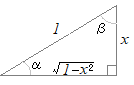
≪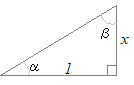 右図のような直角三角形を考えると
右図のような直角三角形を考えると