|
《解説》 ○ 素数 1より大きい整数のうち,1と自分自身以外の整数では割り切れないような整数を素数といいます. ○ エラトステネスのふるい 素数を求める方法として,古来有名なものに「エラトステネスのふるい」があります.(エラトステネスはギリシア時代の人の名) もし1を素数に含めてしまうと,素因数分解が何通りでもできてしまい,素因数分解の理論がグチャグチャになってしまいます.
例えば,1を素因数分解に含めない普通の立場では6の素因数分解は2×3のただ1通りに決まりますが,1を素因数に含めてしまうと1×2×3, 12×2×3, 13×2×3, 14×2×3, ...と素因数分解の仕方が何通りでもあることになり混乱が起こります. その方法は, 1は素数とはしないので除外する.(意外と忘れやすいので注意.中学生では,約束だと思えばよい.) 2を残して2で割り切れるものを除外する.3を残して3で割り切れるものを除外する. (4は除外されている.) 5を残して5で割り切れるものを除外する. (6は除外されている.) 7を残して7で割り切れるものを除外する.... のように進めていき,残った数が素数と考えます. 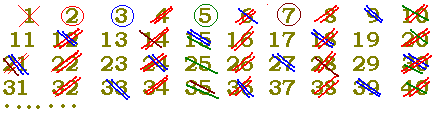 |
○どんな正の整数Nでも,1と自分自身Nで必ず割り切れますが,1と自分自身N「以外の」整数では割り切れないとき,その整数Nは「素数」といいます.
【素数でないものの例】
▼ 4は,(1, 4以外で)2で割り切れるから「素数ではない」. ▼ 6は,(1, 6以外で)2, 3で割り切れるから「素数ではない」. ▼ 9は,(1, 9以外で)3で割り切れるから「素数ではない」. 【素数であるものの例】 ◎ 2は,1, 2以外の整数では割り切れないから「素数です」. ◎ 3は,1, 3以外の整数では割り切れないから「素数です」. ◎ 5は,1, 5以外の整数では割り切れないから「素数です」. 【間違いやすいもの】 ▼ 1は,上で解説したように「素数に入れません」. ▼ 0は,正の整数でないから「素数に入れません」.
《できれば覚えた方がよい:100までの素数》
1は素数ではない.(これは約束) 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97 は素数です. |