|
○ 右図1の直線の方程式は y=x−1 …(1) のようにy について解かれた形で表されることが多いが, x−2y−2=0 …(2) のように x , y の関係式として表されることもある. ○ (1)のように, y=f(x) の形で,y について解かれた形の関数を陽関数といい,(2)のように f(x , y)=0 という形で x , y の関係式として表される関数を陰関数という. ■ 点が曲線上にあるとは 方程式が(1)(2)どちらの形であっても,x=−1, 0 , 1 , 2 , … を順に代入していくと,y=−,−1 ,− , 0 , … が順に求まり,これらの点を結ぶと直線が得られる.一般に,ある点が与えられた方程式を表されるグラフ(曲線や直線)上にあるかないかは,次のように調べることができる.
○
ある点 (p, q)がy=f(x)のグラフ上にある⇔q=f(p) ある点 (p, q)がy=f(x)のグラフ上にない⇔q≠f(p) ○ ある点 (p, q)がf(x, y)=0のグラフ上にある⇔f(p, q)=0 ある点 (p, q)がf(x, y)=0 のグラフ上にない⇔f(p, q)≠0 |
図1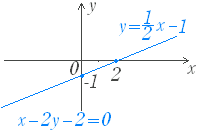 y=2x+1, y=3x2, y=4 陰関数の例 y−2x−1=0, y−3x2=0, y−4=0 図2 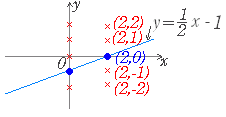 2≠×2−1 だから (2, 2) は y=x−1 上にない. 1≠×2−1 だから (2, 1) は y=x−1 上にない. 0=×2−1 だから (2, 0) は y=x−1 上にある. −1≠×2−1 だから (2 ,−1) は y=x−1 上にない. −2≠×2−1 だから (2 ,−2) は y=x−1 上にない. 陰関数で表示されているときも同様に,「代入したときに方程式が成り立てばグラフ上にある」「代入したときに方程式が成り立たなければグラフ上にない」と判断できる. 2−2×2−2≠0 だから (2, 2) は x−2y−2=0 上にない. 2−2×1−2≠0 だから (2, 1) は x−2y−2=0 上にない. 2−2×0−2=0 だから (2, 0) は x−2y−2=0 上にある. 2−2×(−1)−2≠0 だから x−2y−2=0 上にない. 2−2×(−2)−2≠0 だから x−2y−2=0 上にない. |
|
■ 1つの x に対応する y が2つあるとき ○ 右図3のように,1つの x に対応する y が2つあるグラフの方程式は,y=f(x) の形(陽関数)で書けば 陰関数を用いれば,y2=x あるいは x−y2=0 と書くことができる. ○ 右図4は原点を中心とする半径5の円のグラフであるが,この円は縦線と2箇所で交わるので,1つの x に対応する y が2つあり,円の方程式は1つの陽関数では表せない. ○ 右図5において,原点を中心とする半径5の円の方程式を求めてみよう. 円周上の点 P の座標を (x, y) とおくと,ピタゴラスの定理(三平方の定理)により, x2+y2=52 …(A) が成り立つ. 上半円については,y≧0 なので, y= …(B) 下半円については,y≦0 なので, y=− …(C) と書けるが,通常は円の方程式を(A)の形で表す. ※ 点 (3, 4) は,32+42=52 を満たすのでこの円周上にある. |
図3  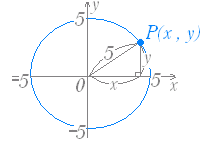 |
| ■ 円の方程式
原点を中心とする半径 r の円(円周)の方程式は
x2+y2=r2 …(1)  (x−a)2+(y−b)2=r2 …(2) 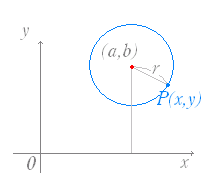 ※ 初歩的な注意 ○ (2)において,点 (a, b) を中心とする半径 r の円の方程式が (x−a)2+(y−b)2=r2 点 (−a ,−b) を中心とする半径 r の円の方程式が (x+a)2+(y+b)2=r2 点 (a ,−b) を中心とする半径 r の円の方程式が (x−a)2+(y+b)2=r2 のように,中心の座標 (a, b) は,円の方程式では見かけ上の符号が逆になる点に注意. ○ (1)(2)とも右辺は r2 なので, 半径が 2 → 右辺は 4 半径が 3 → 右辺は 9 半径が 4 → 右辺は 16 半径が → 右辺は 2 半径が → 右辺は 3 などになる点に注意 |
(証明) (1)← 原点を中心とする半径 r の円周上の点を P(x, y) とおくと,直角三角形の横の長さが x,縦の長さが y の直角三角形の斜辺の長さが r となるのだから, x2+y2=r2 が成り立つ. (別の証明):2点間の距離の公式 2点 A(a, b), B(c, d) 間の距離は, =r より x2+y2=r2 ※ 点 P が座標軸上(通俗的に言えば,赤道上または北極,南極の場所)にあるとき,直角三角形にならないが,たとえば x 軸上の点 (r, 0) についても,r2+02=r2 が成り立つ.このように,座標軸上の点については直角三角形はできないが,この方程式は成り立つ. ※ 点 P が第2,第3,第4象限にあるとき,x, y 座標が負になることがあるので,正確に言えば,直角三角形の横の長さが |x|,縦の長さが |y| とすべきであるが,このように説明すると経験上,半数以上の生徒が授業を聞く意欲をなくすようである(絶対値アレルギー?).(1)においては,x, y が正でも負でも2乗するので結果はこれでよい. (2)← 2点 A(a, b), P(x, y) 間の距離は, だから,この値が r に等しいことが円周上にある条件となる. =r より (x−a)2+(y−b)2=r2 |
| 例題 (1) 原点を中心とする半径4の円の方程式を求めよ. (解答) x2+y2=16 (2) 点 (−5, 3) を中心とする半径 2 の円の方程式を求めよ (解答) (x+5)2+(y−3)2=4 |
(3) 円 (x−4)2+(y+1)2=9 の中心の座標と半径を求めよ. (解答) 中心の座標 (4 ,−1),半径 3 |
