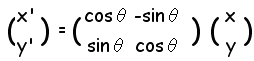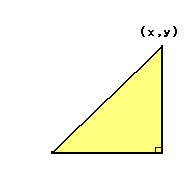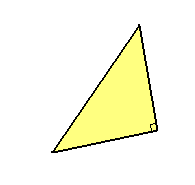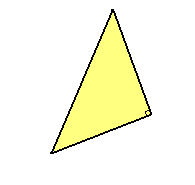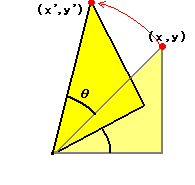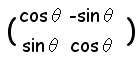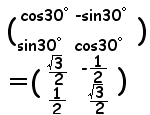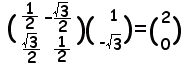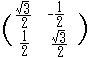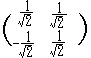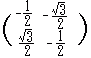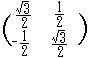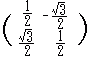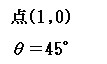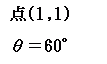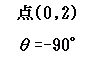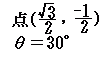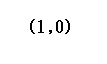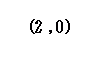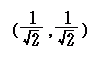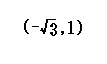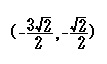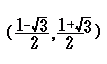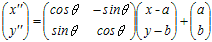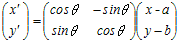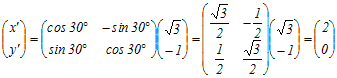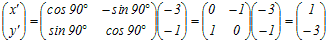■回転移動の１次変換
 
■
点（ｘ，ｙ）を原点の周りに角θだけ回転すると点（ｘ’，ｙ’）に移されるものすると，
ｘ’＝ｘcosθ-ysinθ
ｙ’＝ｘsinθ+ycosθ
すなわち




■
説明方法が幾つかありますが，一長一短ですので，各自の思考パターンに合うもので納得しましょう。全部読む必要はありません。↓→

 ■説明1

順に選んで下さい

■説明２
まず，基本ベクトル
＝(1,0)，＝(0,1)
を角θ回転すると
＝(cosθ,sinθ)，＝(-sinθ,cosθ)
となります。

次に，

＝ｘ+ｙ
であった点は
＝ｘ＋ｙ
に移りますが，

＝(cosθ,sinθ)，＝(-sinθ,cosθ)

により，
＝ｘ(cosθ,sinθ)+ｙ(-sinθ,cosθ)
＝(xcosθ-ysinθ，xsinθ+ycosθ)
 ■説明３
他のページに次の記述があります。
ある1次変換によって，点（１，０）が（ａ，ｃ）に点（０，１）が点（ｂ，ｄ）に移されるとき， １次変換の行列は，
＝(1,0)，＝(0,1)が
＝(cosθ,sinθ)，＝(-sinθ,cosθ)
に移されるのだから，
■(参考)
三角関数の加法定理との関係
x=ｒcosα，y=rsinα・・(1)
ｘ’＝ｒcos(α+θ)，ｙ’＝ｒsin(α+θ)・・(2)において
三角関数の加法定理
sin(α+β)＝sinαcosβ+cosαsinβ
cos(α+β)＝cosαcosβ-sinαsinβ
を用いれば，
ｘ’＝ｒ(cosαcosθ-sinαsinθ)
　　＝ｒcosαcosθ-ｒsinαsinθ
　　＝ｘcosθ-ｙsinθ
ｙ’＝ｒ(sinαcosθ+cosαsinθ)
　　＝ｒsinαcosθ+ｒcosαsinθ
　　＝ｙcosθ+ｘsinθ＝ｘsinθ+ｙcosθ
--
例題
１
原点のまわりに30°回転する１次変換の行列は，
２
点(１，−√3)を原点のまわりに60°回転した点の座標は，
により，（２，０）になります。
--［問題1］
原点のまわりに次の角度だけ回転することを表す１次変換の行列を求めなさい。（初めに角度を選び，次に行列を選びなさい。正しければ消えます。）
 
[角度]





［行列］
　　　
　　　
　　　
--［問題2］
次の点を原点のまわりに角度θだけ回転した点の座標を求めなさい。（初めに問題を選び，次に選択肢を選びなさい。正しければ消えます。）---計算用紙が必要です。
 
[問題]
　　
　　
　　
 ［選択肢］
　　
　　
　　

■　原点以外の点の周りの回転
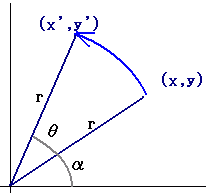
　点P(x, y)を点A(a, b)の周りに角θだけ回転した点を
Q(x”, y”)とすると
（解説）
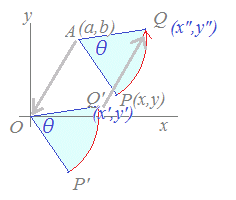
　原点の周りの回転移動の公式を使って，一般の点A(a, b)の周りの回転の公式を作ります．
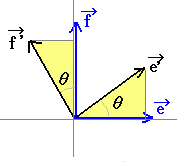
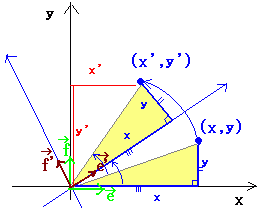
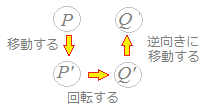
　すなわち，右図のように，扇形APQと合同な図形を扇形OP’Q’として作り，次にQ’を平行移動してQを求めます．
(1) はじめに，点A(a, b)を原点に移す平行移動により，点Pが移される点を求めると
P(x, y) → P’(x−a, y−b)
(2) 次に，原点の周りに点P’(x−a, y−b)を角θだけ回転すると

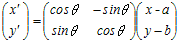
(3) 求めた点Q’(x’, y’)を平行移動して元に戻すと


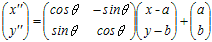
【例１】
　点P(, 1)を点A(0, 2)の周りに30°だけ回転するとどのような点に移されますか．
（解答）
(1)　点A(0, 2)を原点に移す平行移動（x方向に0，y方向に−2）により，
P(, 1) → P’(, −1)
と移される．
(2)　P’(, −1)を原点の周りに30°だけ回転してできる点Q’(x’, y’)の座標は次の式で求められる

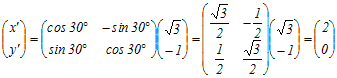
(3)　最後に，点Q’(x’, y’)を逆向きに平行移動（x方向に0，y方向に2）すると
Q’(2, 0) → Q(2, 2)…（答）
【例２】
　原点O(0, 0)を点A(3, 1)の周りに90°だけ回転するとどのような点に移されますか．
（解答）
(1)　点A(3, 1)を原点に移す平行移動（x方向に−3，y方向に−1）により，
O(0, 0) → P’(−3, −1)
と移される．
(2)　P’(−3, −1)を原点の周りに90°だけ回転してできる点Q’(x’, y’)の座標は次の式で求められる

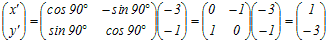
(3)　最後に，点Q’(x’, y’)を逆向きに平行移動（x方向に3，y方向に1）すると
Q’(1, −3) → Q(4, −2)…（答）
［問題３］次の各点の座標を求めてください．（正しいものを選んでください）
(2)
　点P(4, 0)を点A(2, 2)の周りに60°だけ回転してできる点
○...複素数の回転
○===高卒〜大学数学基礎メニューに戻る　
...メニューに戻る